基于数据驱动的综合能源系统多场景两阶段分布式鲁棒优化模型

鲁棒优化是应对数据不确定性的一种优化方法，但单阶段鲁棒优化过于保守。为了解决这一问题，引入了两阶段鲁棒优化(Two-stage Robust Optimization)以及更一般的多阶段鲁棒优化，其核心思想是将决策问题分为两个阶段。第一阶段是进行初步决策，第二阶段是根据第一阶段的决策结果制定更好的决策策略，应对数据不确定性的影响。这种方法可以降低保守性，提高鲁棒性。

两阶段鲁棒优化模型在含有风电、光伏、储能的综合能源系统以及主动配电网中均得到了很多应用。本文采用基于数据驱动的分布鲁棒方法处理了 DG 和负荷的不确定性。

优化模型：

一、程序目标函数：

第一阶段

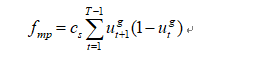
Cs是启停成本系数，一阶段目标是微燃机启停成本，u代表发电机状态变量。

第二阶段

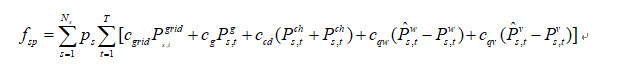
分别是电网购电成本、发电机运行成本、蓄电池老化成本（或者运维）、弃风和弃光成本。

模型包含以下约束：

约束1：微燃机出力约束

约束2：爬坡约束。

约束3：储能充放电约束

约束4：储能初始能量和最终能量一致

约束5：储能soc范围约束

约束6.电功率平衡约束

约束7.热功率平衡

二、部分程序实例：

%function [p_wt,p_pv,p_load,x,UB,p_ch,p_dis,p_g,p_buy,p_sell]=SP2(ee_bat_int, p_wt_int,p_pv_int,p_g_int,LB,yita)%决策变量% p_ch=sdpvar(24,4);p_dis=sdpvar(24,4);p_gl=sdpvar(24,4);%uu_ch=binvar(24,4);uu_dis=binvar(24,4);uu_m=binvar(24,4);%充放电状态、发电机状态% p_buy=sdpvar(24,4);%购电变量% p_wt=sdpvar(24,4);p_pv=sdpvar(24,4);%实际参与风、光% p_g=sdpvar(24,4);%不确定性变量psp=sdpvar(1,4);psd=sdpvar(1,4);sigmap=binvar(1,4);sigmad=binvar(1,4);ps=sdpvar(1,4);u_g=[uu_m(:,1)' uu_m(:,2)' uu_m(:,3)' uu_m(:,4)'];u_ch=[uu_ch(:,1)' uu_ch(:,2)' uu_ch(:,3)' uu_ch(:,4)'];u_dis=[uu_dis(:,1)' uu_dis(:,2)' uu_dis(:,3)' uu_dis(:,4)'];%风光出力和电价（以春季典型日为例）ps0=[22.7; 15.6; 38.05; 23.65]./100;%场景概率price=[0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.9 1.35 1.35 1.35 0.9 0.9 0.9 0.9 0.9 0.9 0.9 1.35 1.35 1.35 1.35 1.35 0.48];%电价constraints=[];%约束开始load=p_l';%不确定约束constraints=[constraints,sum(psp+psd)<=theta1];constraints=[constraints,psp+psd<=thetaw];constraints=[constraints,sigmap+sigmad<=1];constraints=[constraints,0<=psp<=sigmap*theta1];constraints=[constraints,0<=psd<=sigmad*theta1];constraints=[constraints,ps==ps0'+psd+psp];lam1=sdpvar(96,1);lam11=sdpvar(96,1);lam12=sdpvar(96,1);lam120=sdpvar(96,1);lam2=sdpvar(192,1);lam21=sdpvar(192,1);lam3=sdpvar(4,1);lam4=sdpvar(96,1);lam41=sdpvar(96,1);lam5=sdpvar(96,1);lam51=sdpvar(96,1);lam6=sdpvar(96,1);%设定对偶变量beta1=sdpvar(96,1);beta11=sdpvar(96,1);beta12=sdpvar(96,1);beta120=sdpvar(96,1);beta2=sdpvar(192,1);beta21=sdpvar(192,1);beta3=sdpvar(4,1);beta4=sdpvar(96,1);beta41=sdpvar(96,1);beta5=sdpvar(96,1);beta51=sdpvar(96,1);beta6=sdpvar(96,1);beta7=binvar(672,1);beta8=binvar(288,1);%大m条件中的01变量x=[];P=[];pw=[];pv=[];for i=1:4x=[x,p_buy(:,i)' p_g(:,i)' p_ch(:,i)' p_dis(:,i)' p_gl(:,i)' p_wt(:,i)' p_pv(:,i)'];%x变量% P=[P,ps(i).*price ps(i)*cg.*ones(1,24) ps(i)*ccn.*ones(1,48) zeros(1,24) -ps(i)*cq.*ones(1,48)];P=[P,price cg.*ones(1,24) ccn.*ones(1,48) zeros(1,24) -cq.*ones(1,48)];pw=[pw,ps(i).*p0_wt(:,i)'];pv=[pv,ps(i).*p0_pv(:,i)'];endx=x';%下面相关的计算参数和参考资料一致%B=repmat([c_wt_om.*ones(1,24) c_pv_om.*ones(1,24) zeros(1,24)]',1,4);Q1=[zeros(24,24) eye(24) zeros(24,120) zeros(24,504);zeros(24,168) zeros(24,24) eye(24) zeros(24,120) zeros(24,336);zeros(24,336) zeros(24,24) eye(24) zeros(24,120) zeros(24,168);zeros(24,504) zeros(24,24) eye(24) zeros(24,120)];lint=zeros(tn);for i=1:tn-1lint(i,i)=-1;lint(i,i+1)=1;endlint(tn,tn)=-1;lint(tn,1)=1;obj_sp=-sum(Cz'.*ps);ops=sdpsettings('solver','gurobi');reuslt=optimize(constraints,obj_sp,ops);%ops.cplex.exportmodel='abcd.lp';%obj_o=double(obj_o);%p_ch=double(p_ch);p_dis=double(p_dis);p_buy=double(p_buy);;p_g=double(p_g);ps=value(ps);Q=value(obj_sp);UB1=LB-yita-Q;

运行结果：

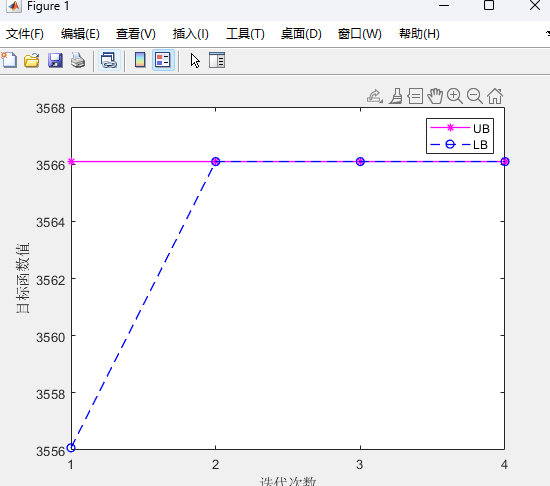
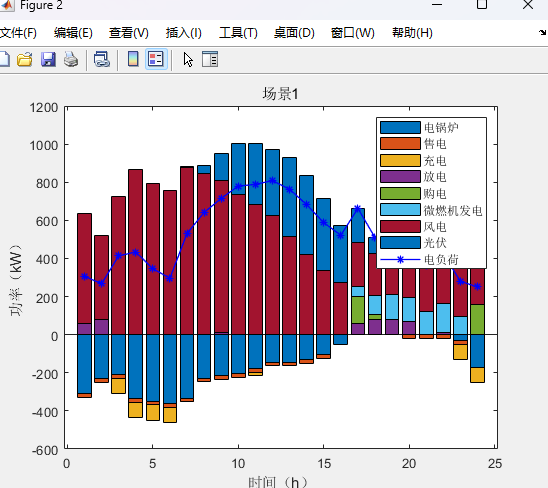
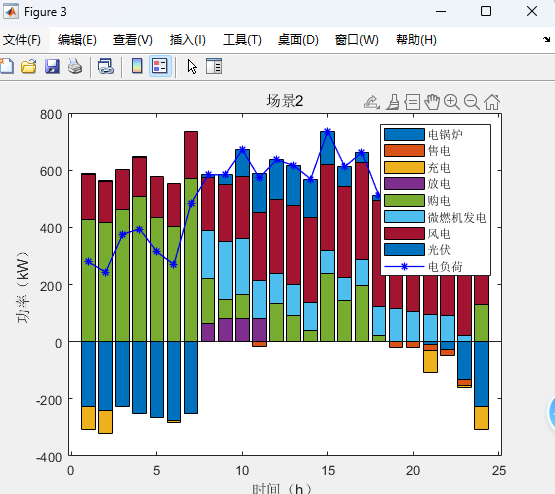
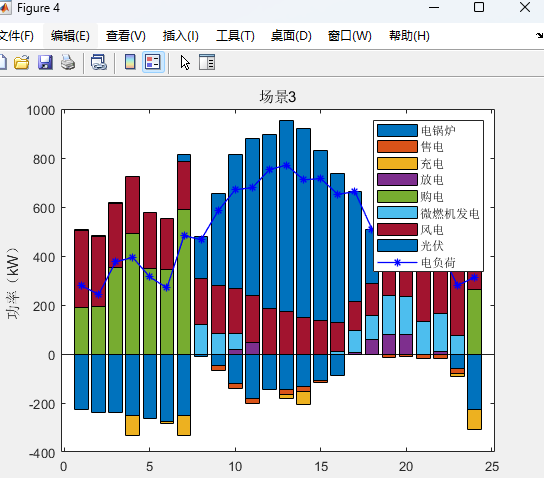
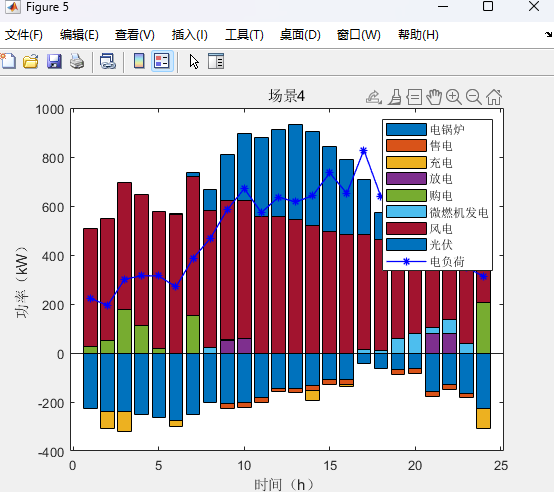
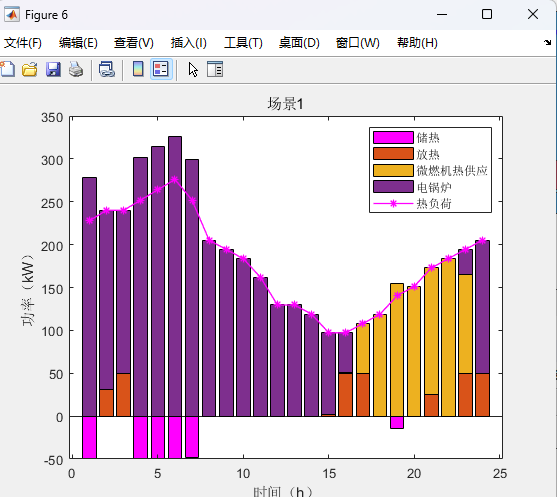
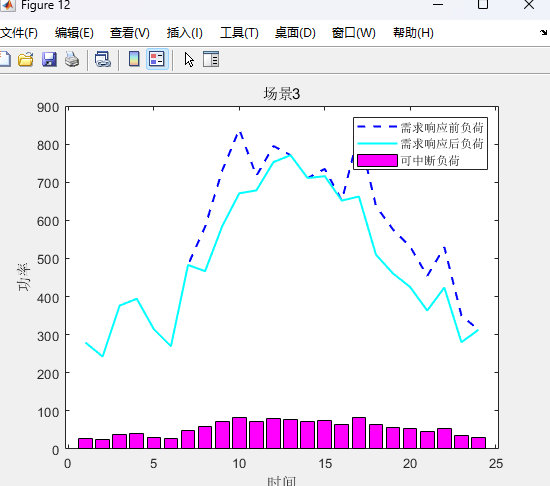
两阶段分布式优化模型代码详情见原文：

https://mp.weixin.qq.com/s/WLhU1032VCM-YYJtQClurw