第五章:路径规划算法
欢迎回来,未来的机器人专家-=≡(・ω・)
在之前的章节中,我们已为机器人配备了核心知识:它能够跟踪自身的机器人状态/位姿,利用环境表示(栅格地图)理解周围环境,通过机器人运动模型预测运动轨迹,并借助定位滤波器精确定位。
现在,机器人已掌握"
自身位置“和”环境信息"。但若要让其从A点移动到B点呢?
当存在墙壁或障碍物时,它无法直线行进。它需要一份"移动计划"。
这正是路径规划算法的用武之地!
什么是路径规划算法?
想象我们试图在一个陌生城市中从当前位置前往朋友家。
打开手机GPS导航,它不仅能显示直线距离,还会规划出避开建筑、湖泊和单行道的实际路线。
路径规划算法就如同机器人的高级GPS系统。
其核心任务是:基于地图(栅格地图)信息避开障碍物,为机器人找到从起点到目标点的安全高效移动序列(即"路径"),通常还需优化特定指标(如最短路径或最快路径)。
若无路径规划,机器人只会漫无目的游荡或直接撞上首个障碍物!这是指导机器人高层移动决策的"大脑"。
路径规划的核心概念
理解机器人路径规划需掌握以下关键概念:
| 概念 | 描述 | 类比 |
|---|---|---|
起点 | 机器人的初始位置和朝向(基于机器人状态/位姿) | GPS上标注的当前位置 |
目标点 | 机器人需要到达的最终位置和朝向 | 朋友家的详细地址 |
障碍物 | 机器人不可进入或穿过的区域,通常定义在栅格地图中 | 地图上的建筑物、河流或禁行区 |
路径 | 引导机器人从起点到目标点的中间点或状态序列,需避开障碍物 | GPS推荐的蓝色导航路线 |
代价 | 表示路径"成本"的数值,可以是距离、时间、能耗或其组合 | GPS显示的预计行程时间或里程数 |
优化 | 根据特定目标(如最短路径、最快路径)寻找最小化(或最大化)代价的路径 | 在GPS中选择"最短路线"或"最快路线"选项 |
如何使用路径规划算法(A*算法示例)
PythonRobotics包含多种路径规划算法。
我们从A*(A-Star)搜索算法开始,这是一种广为人知且直观的算法,尤其适用于栅格地图。
假设我们需要机器人在存在障碍物的地图中从(10, 10)米移动到(50, 50)米。
以下是使用PathPlanning/AStar/a_star.py中AStarPlanner类设置并运行A*规划器的典型流程:
import matplotlib.pyplot as plt # 可视化工具
from PathPlanning.AStar.a_star import AStarPlanner# 1. 定义起点和目标点坐标(单位:米)
sx, sy = 10.0, 10.0 # 起点X,Y
gx, gy = 50.0, 50.0 # 目标点X,Y# 2. 定义地图属性及机器人尺寸
grid_size = 2.0 # 每个栅格单元为2.0m×2.0m
robot_radius = 1.0 # 机器人视为半径1.0m的圆形# 3. 定义障碍物(障碍物中心点坐标)
# 简单示例:创建墙状障碍物
ox, oy = [], []
for i in range(10, 40): # 在x=20处创建垂直墙(y从10到39)ox.append(20.0)oy.append(float(i))
for i in range(20, 50): # 在y=30处创建水平墙(x从20到49)ox.append(float(i))oy.append(30.0)# 4. 创建A*规划器对象
planner = AStarPlanner(ox, oy, grid_size, robot_radius)# 5. 执行路径规划!
print("开始路径规划...")
# rx, ry将存储规划路径的x,y坐标
rx, ry = planner.planning(sx, sy, gx, gy)if rx: # 找到路径时print(f"找到包含{len(rx)}个路径点的路径")# 可进行可视化:# plt.plot(ox, oy, ".k") # 绘制障碍物# plt.plot(sx, sy, "og") # 绘制起点# plt.plot(gx, gy, "xb") # 绘制目标点# plt.plot(rx, ry, "-r") # 绘制路径# plt.grid(True); plt.axis("equal"); plt.show()
else:print("未找到可行路径!")
代码解析:
- 创建
AStarPlanner对象时需提供障碍物坐标(ox,oy)、栅格尺寸(grid_size,用于生成内部栅格地图)和机器人半径(robot_radius,确保与障碍物保持安全距离)。 planning()方法接收起点(sx, sy)和目标点(gx, gy)坐标,返回表示最优路径的rx, ry坐标列表。若目标点被阻塞则返回None。
输出结果rx, ry即为机器人应遵循的详细路径坐标序列
路径规划算法内部原理(A*算法拆解)
🎢启发式函数
启发式函数是一种“经验法则”,用于估计从当前状态到目标状态的近似距离,帮助算法更快找到最优路径。比如在地图导航中,启发式函数可以简单计算两点间的直线距离。
A*算法是一种智能路径搜索算法,通过结合当前路径成本和预估剩余距离(启发式函数)来高效找到最优路径,类似导航软件选择最快路线。
A*算法与BFS
A*算法可以看作BFS的智能升级版。
- BFS会
盲目扩展所有可能路径 - 而A通过启发式函数优先探索更接近目标的路径。
两者都用队列管理待探索节点,但A的队列按“实际成本+预估成本”排序,效率更高。
A*算法高层流程
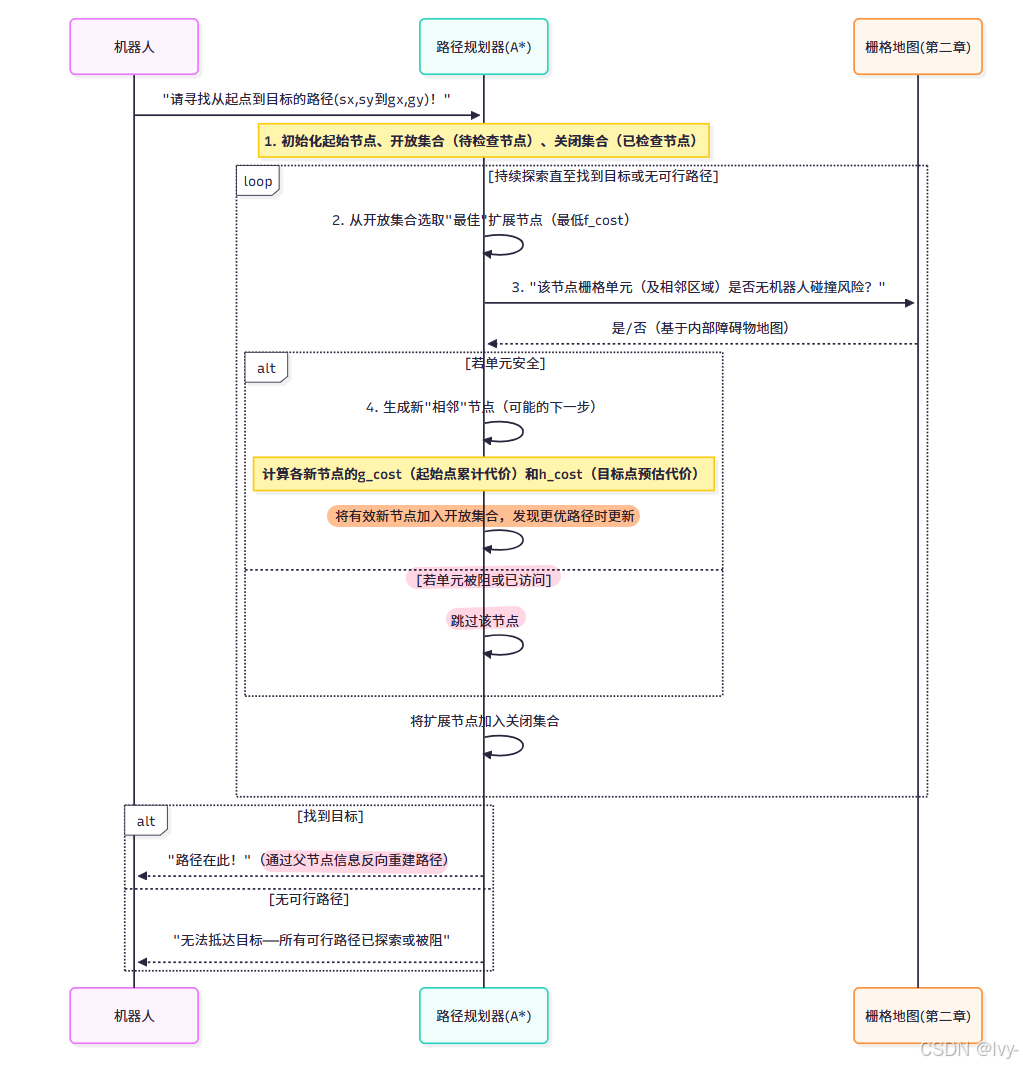
A*代码核心组件
AStarPlanner类管理地图、障碍物及搜索过程,关键部分如下:
1. Node类:
A*算法中,"节点"代表算法正在考虑的栅格单元。其不仅包含x, y坐标,还存储搜索所需信息(详见第六章:路径规划搜索节点)。
PathPlanning/AStar/a_star.py中的简化实现:
class AStarPlanner:# ... (其他代码) ...class Node:def __init__(self, x, y, cost, parent_index):self.x = x # 栅格单元X索引self.y = y # 栅格单元Y索引self.cost = cost # g_cost(从起点到本节点的累计代价)self.parent_index = parent_index # 到达本节点的父节点索引(用于路径重建)
解析:
x,y:栅格索引(非实际米制坐标),由AStarPlanner内部转换。cost:即g_cost(从起点到当前节点的实际累计代价)。parent_index:关键回溯信息,记录到达当前节点的前一节点。找到目标后,沿此索引逆向重建完整路径。
2. 运动模型(定义可行移动方向):
栅格化A*的"运动模型"定义了机器人可移动的相邻单元。
a_star.py中的get_motion_model()静态方法定义了8个可能方向(上下左右及对角线):
class AStarPlanner:# ... (其他代码) ...@staticmethoddef get_motion_model():# dx, dy, costmotion = [[1, 0, 1], # 右移(X+1,Y+0),代价1[0, 1, 1], # 上移(X+0,Y+1),代价1[-1, 0, 1], # 左移(X-1,Y+0),代价1[0, -1, 1], # 下移(X+0,Y-1),代价1[-1, -1, math.sqrt(2)], # 对角线(X-1,Y-1),代价√2[-1, 1, math.sqrt(2)], # 对角线(X-1,Y+1),代价√2[1, -1, math.sqrt(2)], # 对角线(X+1,Y-1),代价√2[1, 1, math.sqrt(2)]] # 对角线(X+1,Y+1),代价√2return motion
解析:
- 每个子列表
[dx, dy, cost]描述一种移动方式,dx和dy为栅格索引变化量。 cost为移动代价。水平/垂直移动代价为1,对角线移动为实际距离√2,确保算法找到真正最短路径。
3. 代价计算(f_cost = g_cost + h_cost):
A*算法通过"启发式函数"引导搜索方向,避免盲目探索。每个节点包含两种代价:
| 代价类型 | 描述 | 类比 |
|---|---|---|
g_cost | 从起点到当前节点的实际代价 | 已从起点行走的实际距离 |
h_cost | 当前节点到目标的预估代价(启发式) | 预估剩余距离(如直线距离猜测) |
f_cost | 总预估代价(g_cost + h_cost) | 路径总长度的综合预估 |
A*算法始终选择开放集合中f_cost最低的节点扩展
a_star.py中的calc_heuristic方法通过欧氏距离计算h_cost:
import mathclass AStarPlanner:# ... (其他代码) ...@staticmethoddef calc_heuristic(n1, n2):# n1: 当前节点, n2: 目标节点# 计算两栅格点间的直线距离d = math.hypot(n1.x - n2.x, n1.y - n2.y)return d
解析:
n1.x - n2.x和n1.y - n2.y为坐标差。math.hypot()计算直角三角形斜边长度,作为引导A*高效搜索的"启发式估计"。
4. 碰撞检测(verify_node):
规划器需确认新栅格单元的安全性,包括检查地图边界及障碍物(基于栅格地图生成的obstacle_map),并考虑机器人半径的安全距离。
class AStarPlanner:# ... (其他代码) ...def verify_node(self, node):# 将栅格索引转换为实际坐标px = self.calc_grid_position(node.x, self.min_x)py = self.calc_grid_position(node.y, self.min_y)# 1. 检查是否超出地图边界if not (self.min_x <= px < self.max_x and self.min_y <= py < self.max_y):return False# 2. 检查障碍物碰撞# self.obstacle_map为二维数组(类似栅格地图)# True表示占据/碰撞,False表示空闲if self.obstacle_map[node.x][node.y]: # 简化检测return Falsereturn True # 节点安全
解析:
calc_grid_position将栅格索引转换为实际坐标以进行边界检查。self.obstacle_map为预先生成的障碍物栅格图,若obstacle_map[node.x][node.y]为True,表示该单元存在碰撞风险。
PythonRobotics中的其他路径规划算法
尽管A*在栅格地图中表现优异,PythonRobotics还提供多种适应不同场景的规划算法:
- 动态窗口法(DWA)(PathPlanning/DynamicWindowApproach/dynamic_window_approach.py):一种局部路径规划算法。DWA不预先规划全局路径,而是在实时窗口中评估可行的速度与转向指令,结合机器人
动力学、障碍物规避及目标趋近进行决策。常用于实时避障 - 快速扩展随机树(RRT)(PathPlanning/RRT/rrt.py):基于
采样的算法,通过随机生成节点构建树状结构连接起点与目标。适用于复杂高维空间或狭窄通道环境,克服栅格方法的局限性 - Frenet最优轨迹(FOT)(PathPlanning/FrenetOptimalTrajectory/frenet_optimal_trajectory.py):常用于自动驾驶的高级算法。在"
Frenet坐标系"(与参考路径如道路中线对齐)中生成多项式轨迹,通过优化速度、舒适度及避障等代价选择最优路径
这些算法展示了路径规划技术的多样性,但均以实现安全高效移动为核心目标。
小结
本章深入探讨了路径规划算法的关键作用。作为机器人的"智能导航系统",该算法通过结合栅格地图信息与启发式搜索,在避开障碍物的同时优化路径成本。
我们以A*算法为例,解析了节点扩展、代价计算及碰撞检测的核心机制,并简介了DWA、RRT和Frenet等高级算法
搜索节点作为多数规划算法的核心组件,将在下一章详细剖析其结构与应用逻辑。
下一章:路径规划搜索节点

 226. 翻转二叉树 (深度优先搜索dfs ))
)

)








)
求解MaF1-MaF15及工程应用---盘式制动器设计,提供完整MATLAB代码)
 和 稀疏点云重建的详细步骤:)


)
