最优化理论是计算机科学中一个重要的概念,它用于帮助我们找到最优解(即最小或最大值)的算法。在深度学习中,最优化理论用于帮助深度学习模型找到最优解。
- 训练误差(Training Error):指模型在训练数据上的误差,即使用训练数据计算的损失函数的值。
- 泛化误差(Generalization Error):指模型在新数据上的误差,即使用测试数据计算的损失函数的值。
Adam算法
Adam算法是在RMSProp算法的基础上提出的,并且使用了指数加权平均数来调整学习率。Adam算法被广泛用于神经网络的训练过程中,因为它能够自适应学习率,使得训练过程更加顺畅。
学习率调节器
学习率调节器是在训练神经网络时用来控制学习率的方法,更好的模型更新步骤大小的值。当学习率过大时,模型会振荡或者发散,而当学习率过小时,模型的收敛速度会变慢。学习率调节器的作用就是帮助我们在训练过程中动态调整学习率,以便获得更好的模型训练效果。
学习率衰减(Learning Rate Decay)、指数衰减法(Exponential Decay)、余弦学习率调节(Cosine Annealing)、自定义学习率调节、预热
=============
梯度下降
在使用梯度下降法时,我们需要计算损失函数的梯度。梯度的方向是参数的最佳修改方向,因此我们可以使用梯度的方向来更新参数,从而最小化损失函数。具体来说,在每一步迭代中,梯度下降法会根据当前参数计算损失函数的梯度,然后沿着梯度的反方向更新参数。这样做能使损失函数的值不断减小,直到达到最小值为止。这个过程中参数的更新规则如下:
![]()
在这里,θ 是要被更新的参数,α 是学习率,∇θL 是损失函数 L 关于参数 θ 的梯度。
学习率
学习率 α 是梯度下降法的一个重要超参数。它决定了每一步迭代中参数的更新幅度,也就是说,它决定了梯度下降法的收敛速度。
随机梯度下降法
随机梯度下降法(SGD,Stochastic Gradient Descent)的基本思想是每次迭代中仅使用一个样本来计算梯度,然后根据梯度来调整参数的值。具体来说,在每次迭代中,我们会随机选择一个样本 (xi,yi),并根据当前的参数值 w 计算出损失函数的梯度 ∇L(w;xi,yi)。然后,我们就可以使用梯度下降法的更新公式来调整参数的值:
![]()
其中 w 表示参数的值,α 表示学习率,即每次迭代中我们移动的幅度。每次迭代后,我们会检查函数的值是否已经减小到满足预期的程度,如果是则停止迭代,否则继续迭代。
首先,随机梯度下降法每次迭代中仅使用一个样本计算梯度,这使得计算速度快很多。相比之下,梯度下降法每次迭代中都需要使用所有的样本计算梯度,这使得计算速度要慢很多。
其次,随机梯度下降法每次迭代中仅使用一个样本计算梯度,这使得它比梯度下降法更加稳定。
小批量梯度下降法
小批量随机梯度下降法(Mini-Batch Stochastic Gradient Descent)的基本思路是在每一次迭代中,使用一小部分的随机样本来计算梯度,然后根据梯度来更新参数的值。它的基本流程如下:
首先,初始化参数 w 和 b。然后,在每一次迭代中,随机抽取一小部分的样本来计算梯度。假设我们从训练集中随机抽取了 m 个样本,那么我们可以使用下面的公式来计算梯度:
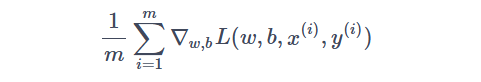
其中 L(w,b,x,y) 是损失函数,∇w,bL(w,b,x,y) 表示对 w 和 b 的梯度。
接下来,根据梯度的值来更新参数的值,使用下面的公式:
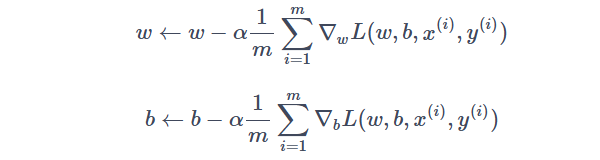
其中 α 是学习率,表示每次更新的步长。最后,重复上述过程直到模型收敛。
动量法
核心思想是让模型的更新更加平稳,从而使学习更加顺畅。具体来说,动量法通过将当前的梯度信息与上一步的梯度信息进行加权平均来减少梯度的震荡。这可以通过使用动量因子 β 来实现。给定一个参数 θ 和当前的梯度 ∇θJ(θ),我们可以使用动量法来更新 θ,公式如下:
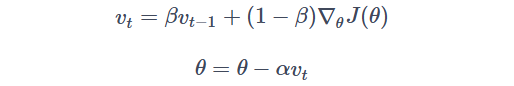
其中,α 是学习率,vt 是梯度的动量,β 是动量因子。在每一步中,我们将当前的梯度与上一步的梯度加权平均起来,并使用这个平均值来更新参数。当 β 很大时,动量较大,这意味着梯度更多地“记住”之前的信息,因此梯度的波动会减少。
AdaGrad算法
Adagrad算法是一种梯度下降法,它是对批量梯度下降法的改进,但并不是对动量法的改进。Adagrad算法的目的是在解决优化问题时自动调整学习率,以便能够更快地收敛。
在优化问题中,我们通常需要找到使目标函数最小的参数值。批量梯度下降法是一种求解此类问题的方法,它在每次迭代时使用整个数据集来计算梯度。然而,批量梯度下降法的收敛速度可能较慢,因为它需要较多的计算。Adagrad算法在每次迭代中,会根据之前的梯度信息自动调整每个参数的学习率。具体来说,使用如下公式:
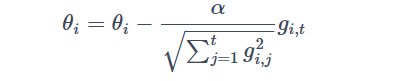
Adagrad算法会在每次迭代中计算每个参数的梯度平方和,并使用这些平方和来调整学习率。这样,Adagrad算法就可以使用较小的学习率来解决那些更难优化的参数,而使用较大的学习率来解决更容易优化的参数。
RMSProp算法
RMSProp 算法通过自动调整每个参数的学习率来解决这个问题。它在每次迭代中维护一个指数加权平均值,用于调整每个参数的学习率。如果某个参数的梯度较大,则RMSProp算法会自动减小它的学习率;如果梯度较小,则会增加学习率。这样可以使得模型的收敛速度更快。
这种算法的计算公式如下:
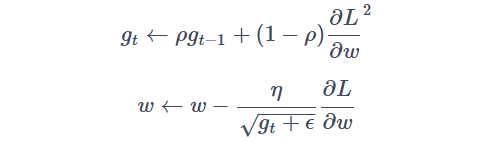
其中 gt 是指数加权平均值,ρ 是衰减率,η 是学习率,ϵ 是为了防止分母为0而添加的一个很小的常数。在每次迭代时,RMSProp 算法会计算参数的梯度平方值的指数加权平均值 gt,然后使用这个值来调整参数的学习率。这样可以使得模型的收敛速度更快,并且能够自动调整学习率。
优点方面,RMSProp算法能够自动调整学习率,使得模型的收敛速度更快。它可以避免学习率过大或过小的问题,能够更好地解决学习率调整问题。实现上看它较为简单,适用于各种优化问题。
缺点方面,它在处理稀疏特征时可能不够优秀。此外,它需要调整超参数,如衰减率 ρ 和学习率 η,这需要一定的经验。还有,收敛速度可能不如其他我们后面会介绍的优化算法,例如 Adam算法。
Adadelta算法
Adadelta是一种自适应学习率的方法,用于神经网络的训练过程中。它的基本思想是避免使用手动调整学习率的方法来控制训练过程,而是自动调整学习率,使得训练过程更加顺畅。
Adadelta算法主要由两部分组成:梯度积分和更新规则。
梯度积分:在每一个时刻,我们可以计算出每一层的梯度。梯度积分即是对这些梯度进行累加,并记录下来。
更新规则:我们通过使用梯度积分来更新每一层的权重。我们使用如下公式来计算权重的更新量:
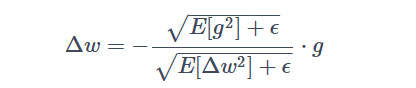
其中,Δw 表示权重的更新量,g 表示当前梯度,E[g2] 表示梯度积分,E[Δw2] 表示权重更新量的积分,ϵ 是一个很小的正数,用于防止分母为 0 的情况。
从缺点来看,它可能会收敛得比较慢,因为它不会显式地调整学习率。此外,它需要维护梯度和权重更新量的积分,可能会增加空间复杂度。
import torch
import torch.nn as nn
import matplotlib.pyplot as plt# 定义一个简单的网络
class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(1, 10)self.fc2 = nn.Linear(10, 1)def forward(self, x):x = self.fc1(x)x = self.fc2(x)return x# 随机生成训练数据
x = torch.randn(100, 1)
y = x.pow(2) + 0.1 * torch.randn(100, 1)# 实例化网络
net = Net()# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = torch.optim.Adadelta(net.parameters())# 记录训练损失
losses = []# 开始训练
for epoch in range(100):# 前向传播 + 反向传播 + 优化output = net(x)loss = criterion(output, y)optimizer.zero_grad()loss.backward()optimizer.step()# 记录损失losses.append(loss.item())# 绘制训练损失图
plt.plot(losses)
plt.show()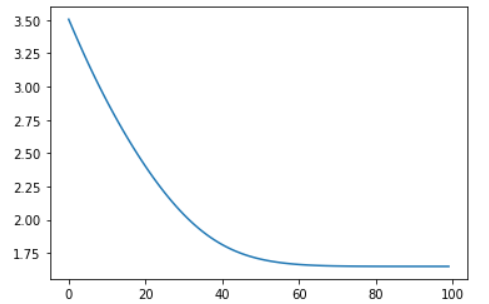



:激活函数)




 ret2dir详细)










![[每周一更]-(第155期):深入Go反射机制:架构师视角下的动态力量与工程智慧](http://pic.xiahunao.cn/[每周一更]-(第155期):深入Go反射机制:架构师视角下的动态力量与工程智慧)