lc17.08

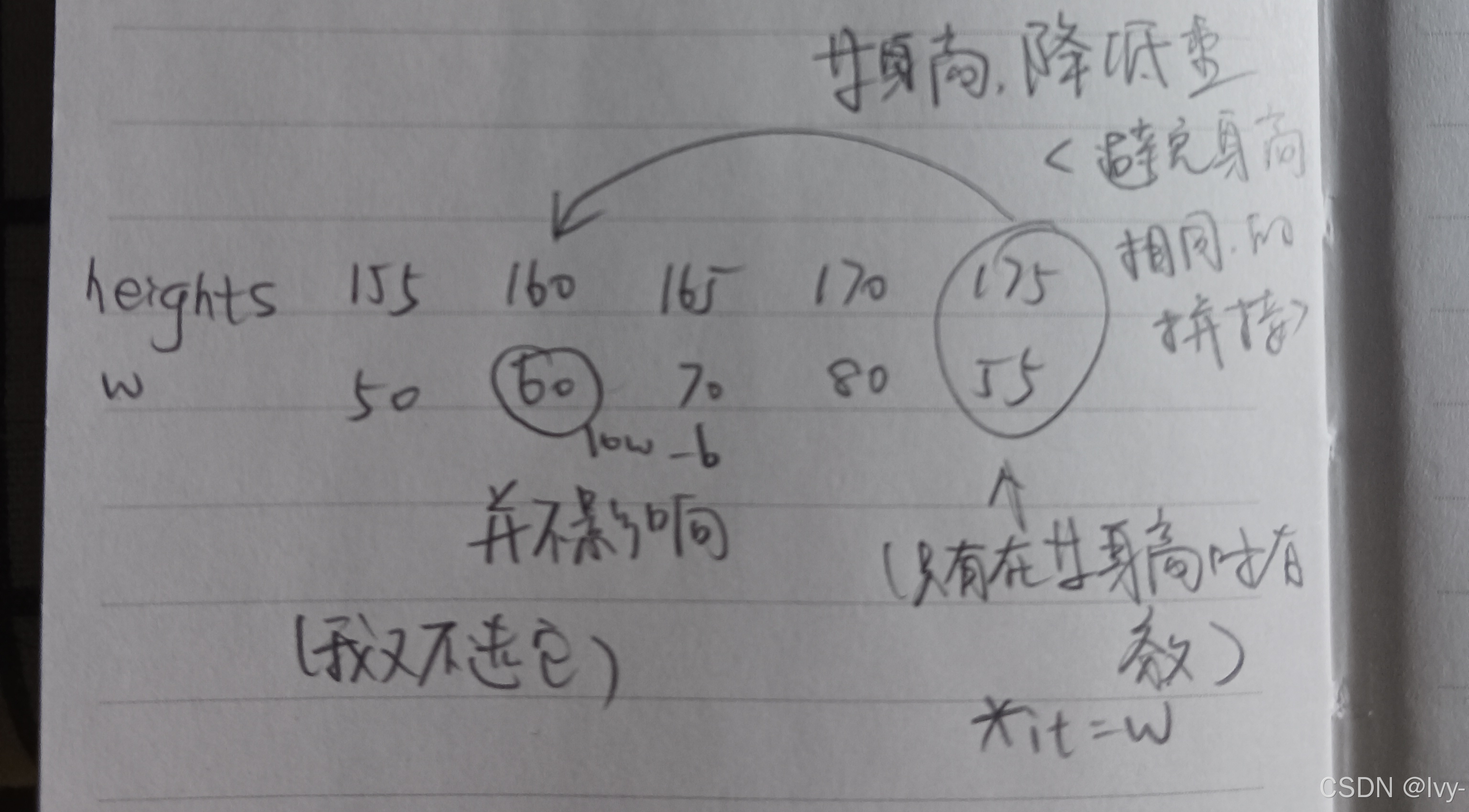
pair按身高升序、相同时体重降序排序

结果是找体重序列的最长递增子序列长度

 

核心：转化为二维最长递增子序列问题求解

        vector<int> dp;
for (auto& p : hw) {
int w = p.second;
auto it = lower_bound(dp.begin(), dp.end(), w);
if (it == dp.end()) {
dp.push_back(w);
} else {
*it = w;
}
}

实际上就是 滚动数组的思想

class Solution {
public:
int bestSeqAtIndex(vector<int>& height, vector<int>& weight)

{
vector<pair<int, int>> hw;
int n = height.size();
for (int i = 0; i < n; ++i)

     {
hw.push_back({height[i], weight[i]});
}
// 先按身高升序排序，身高相同按体重降序排序
sort(hw.begin(), hw.end(), [](const pair<int, int>& a, const pair<int, int>& b) {
if (a.first == b.first) {
return a.second > b.second;
}
return a.first < b.first;
});

// 现在问题转化为在 weight 序列中找最长递增子序列的长度
vector<int> dp;
for (auto& p : hw)

     {
int w = p.second;
auto it = lower_bound(dp.begin(), dp.end(), w);
if (it == dp.end())

           {
dp.push_back(w);
}

            else

            {
*it = w;  //?
}
}
return dp.size();
}
};

lc17.09

微调lc264. 丑数

res[i] = min(min(n7, n3), n5);//填最小

if (res[i] == n7) a++; //每种因子维护自己的下一个

if (res[i] == n3) b++;
if (res[i] == n5) c++;

class Solution {
public:
int getKthMagicNumber(int k)
{
int a = 0, b = 0, c = 0;
int res[k];
res[0] = 1;

for(int i = 1; i < k; i++)
{
int n7 = res[a] * 7, n3 = res[b] * 3, n5 = res[c] * 5;

res[i] = min(min(n7, n3), n5);//填最小

if (res[i] == n7) a++; //每种维护自己的下一个
if (res[i] == n3) b++;
if (res[i] == n5) c++;
}
return res[k-1];
}
};

lc17.18

class Solution

{
public:
vector<int> shortestSeq(vector<int>& big, vector<int>& small) {
unordered_map<int, int> t;
for (auto s : small) t[s]++;

unordered_map<int, int> w;
int req = t.size(), form = 0;
int l = 0, r = 0, n = big.size();
int minL = INT_MAX;
vector<int> res;

while (r < n)

{
int num = big[r];
if (t.count(num))

         {
w[num]++;
if (w[num] == t[num]) form++;
}

while (l <= r && form == req)

        {
int currL = r - l + 1;
if (currL < minL) {
minL = currL;
res = {l, r};
}

int leftNum = big[l];
if (t.count(leftNum))

                {
if (w[leftNum] == t[leftNum])       

                               form--;

w[leftNum]--;
}
l++;
}
r++;
}
return res;
}
};