K最近邻算法
K近邻算法(KNN,k-Nearest Neighbor),每个样本都可以用它的最接近的K个邻近值来代表。
算法说明:
①输入没有标签的新数据,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。
②一般来说,只选择样本数据集中k个最相似的数据。k一般不大于20,最后选择k个数据中出现次数最多的分类,作为新数据的分类。
K近邻算法(KNN,k-Nearest Neighbor),每个样本都可以用它的最接近的K个邻近值来代表。
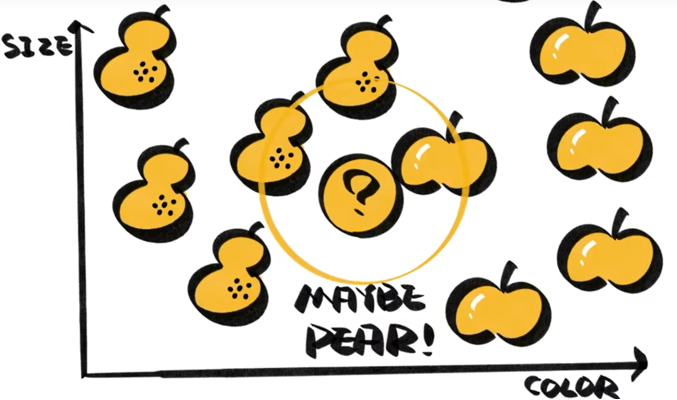
如图所示,包围圈上有两个梨一个苹果,因此问号的应该为梨。
K近邻算法(KNN,k-Nearest Neighbor),每个样本都可以用它的最接近的K个邻近值来代表。
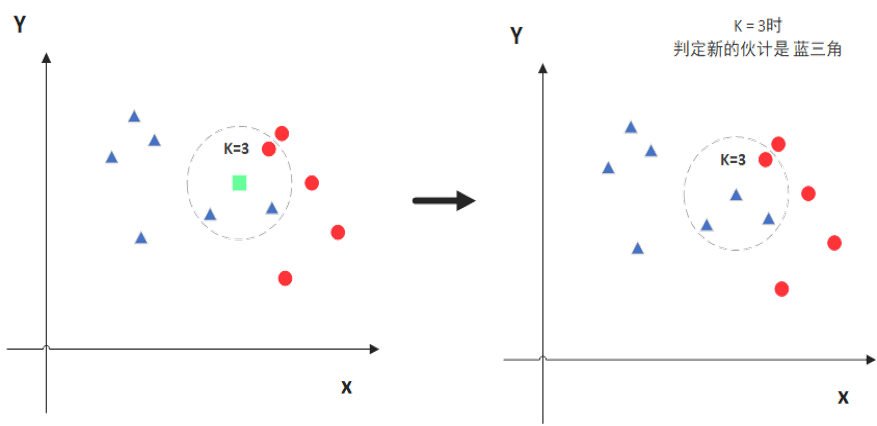
计算已知类别数据集众多点与当前点之间的距离
按照距离递增次序排序
选取与当前点距离最小的k个点
确定前k个点所在类别的出现频率
返回前k个点出现频率最高的类别作为当前点的预测分类
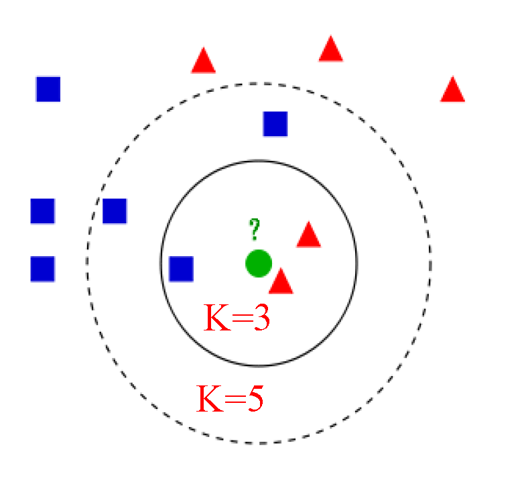
如图所示K=3时?表示红三角;当K=5时?表示蓝方块
距离度量
欧式距离
欧式距离也称欧几里得距离,是最常见的距离度量,衡量的是多维空间中两个点之间的绝对距离 。
在二维和三维空间中的欧式距离的就是两点之间的距离。 ·
二维空间里的欧氏距离公式: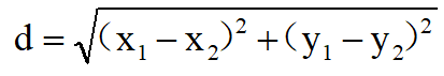
三维空间里的欧氏距离公式: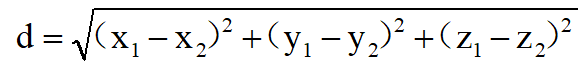
n 维空间里的欧氏距离公式: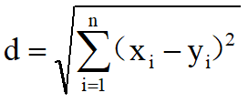
曼哈顿距离
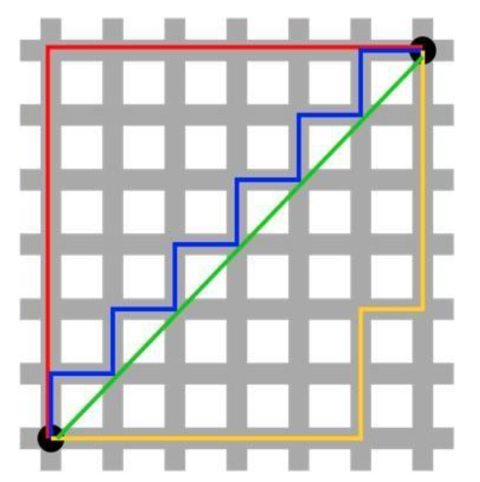
在平面上,坐标(x1,y1)的i点与坐标(x2,y2)的j点的曼哈顿距离为:d(i,j)=|X1-X2|+|Y1-Y2|。
鸢尾花分类
①鸢尾花特征说明: sepal length (cm), sepal width (cm), petal length (cm), petal width (cm)
②基于kNN算法使用sklearn实现鸢尾花分类
加载鸢尾花数据集 iris=datasets.load_iris()
分类的标签 iris.target
特征 iris.feature_names
类别 iris.target_names
划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(iris.data,iris.target,test_size=0.3)
训练模型,创建实例 k=5
knn = KNeighborsClassifier(n_neighbors=5,metric="euclidean")
#n_neighbors近邻数量
#metric距离标准(euclidean欧式距离)
#训练 knntrain = knn.fit(x_train, y_train) print("训练",knntrain)
训练集得分 train_score = knn.score(x_train,y_train)
测试集得分 test_score = knn.score(x_test,y_test)
预测y的值 y_pred = knn.predict(x_test)
from sklearn import datasets
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt# 设置随机种子,保证结果可复现
np.random.seed(0)# 单元格 2:加载鸢尾花数据集并查看
iris = datasets.load_iris()
# 可取消注释查看数据集内容,包含数据、标签、特征名、类别名等信息
# iris
# 查看前 10 条数据
iris.data[:10] 
# 查看数据形状(样本数、特征数)
iris.data.shape
#(150, 4)
# 查看分类标签
iris.target 
# 查看预测结果
y_predict 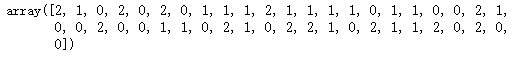
# 用测试集评估模型准确率(标签精度),score 方法会返回模型在测试集上的预测准确率
score = knn.score(x_test, y_test)
score
#0.9777777777777777
# 单元格 7:选择最优 k 值(交叉验证法)
# k 值搜索范围
k_range = range(1, 31)
# 用于存储不同 k 值对应的误差率
k_error = []
x = iris.data
y = iris.target
k_sel = 0
min_error = 1 # 初始化最小误差for k in k_range:knn = KNeighborsClassifier(n_neighbors=k)# 6 折交叉验证,scoring='accuracy' 表示用准确率评估scores = cross_val_score(knn, x, y, cv=6, scoring='accuracy') # 计算误差率(1 - 平均准确率)并添加到列表k_error.append(1 - scores.mean()) if (1 - scores.mean()) < min_error:min_error = 1 - scores.mean()k_sel = k# 输出最优 k 值和对应的最小误差
print("k:", k_sel, "min_error:", min_error)
k: 12 min_error: 0.020000000000000018
# 单元格 8:可视化 k 值与误差率关系
# 绘制折线图,x 轴为 k 值,y 轴为误差率
plt.plot(k_range, k_error)
plt.xlabel('Value of K for KNN')
plt.ylabel('Error')
plt.show() 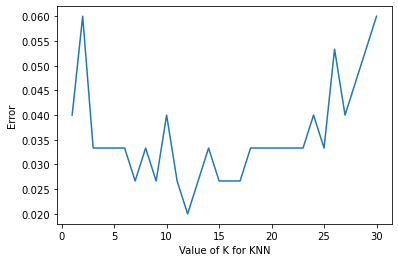
波士顿房价预测
# CRIM、连续型、城镇人均犯罪率
# ZN、连续型、住宅用地中占地面积
# INDUS、连续型、城镇非零售商用土地占比
# CHAS、离散型、查尔斯河虚拟变量(是否邻近河流)
# NOX、连续型、一氧化氮 (NO) 浓度
# AGE、连续型、1940年前建成的自住单位比例
# DIS、连续型、距波士顿5个就业中心的加权距离
# RAD、连连续型、径向高速公路可达性指数
# TAX、每万美元房产税率
# PTRATIO、连续型、城镇师生比例
# LSTAT、连续型、低收入人群占比
#RM、连续型、住宅平均房间数
import numpy as np # 关键修复:导入numpy并简写为np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt# 加载数据集(适配新版sklearn)
boston = fetch_openml(name='boston', version=1, as_frame=True)
X = pd.DataFrame(boston.data, columns=boston.feature_names)
y = pd.Series(boston.target, name='MEDV') # 目标变量:房价中位数(千美元)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
import seaborn as sns
import matplotlib.pyplot as plt
# 绘制特征相关性热力图
corr_matrix = X.join(y).corr()
sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap='coolwarm')# annot在单元格内显示数值
plt.title("特征与房价相关性")
plt.show()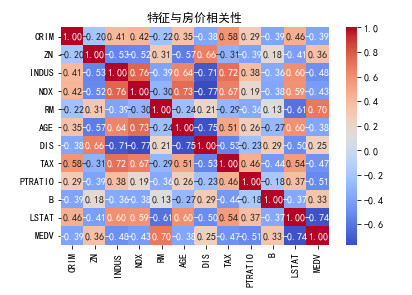
# 将数据转换为均值为 0、标准差为 1的标准正态分布
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score# 划分训练集/测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)# 训练与评估
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred = lr.predict(X_test)print(f"线性回归性能:")
print(f"RMSE: {np.sqrt(mean_squared_error(y_test, y_pred)):.2f}")#反映预测值与真实值的绝对偏差
print(f"R²: {r2_score(y_test, y_pred):.4f}") # 衡量模型拟合优度
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline# 构建流水线(标准化+模型)
pipeline = Pipeline([('scaler', StandardScaler()),('regressor', RandomForestRegressor(random_state=42))
])# 训练与评估
pipeline.fit(X_train, y_train)
y_pred_rf = pipeline.predict(X_test)
print(f"随机森林初始性能:")
print(f"RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_rf)):.2f}")
print(f"R²: {r2_score(y_test, y_pred_rf):.4f}")
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, alpha=0.6, color='blue')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', lw=2)#X轴与Y轴范围
plt.xlabel('真实价格(千美元)')
plt.ylabel('预测价格(千美元)')
plt.title('真实值 vs 预测值')
plt.grid(True)
plt.show()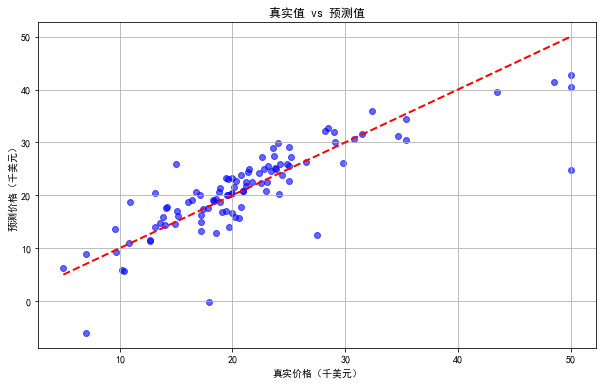
residuals = y_test - y_pred
plt.figure(figsize=(10, 6))
plt.scatter(y_pred, residuals, alpha=0.6, color='green')
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('预测值')plt.ylabel('残差')
plt.title('残差分布图')
plt.show()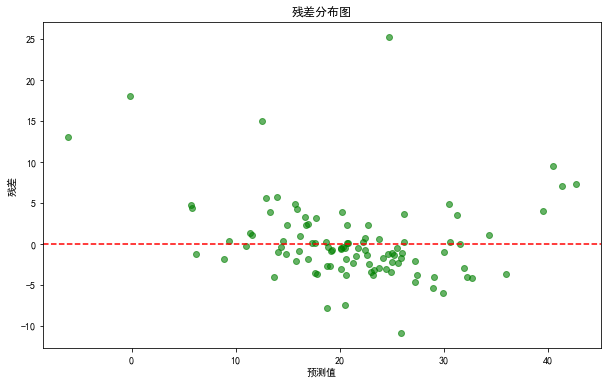


ViDAR:视觉自动驾驶预训练框架)


:总结——基于源码分析的UGUI设计原则与性能优化策略)













