本篇延续上篇内容:
three.js+WebGL踩坑经验合集(9.1):polygonOffsetUnits工作原理大揭秘-CSDN博客
跟polygonOffsetUnits相比,polygonOffsetFactor的系数m要复杂得多,因为它跟平面的视角相关,而不像r那样,在一个固定的设备环境下是一个常量。
说起视角,笔者第一反应是法线跟屏幕所在平面的夹角,然后笔者就试着拿一个只有一个坐标轴旋转的平面来进行测试,但很不幸,锁定了很多条件,都得不到一个期望的“线性”结果。动一下滚轮,调整下camera的position,前面试出来的系数值就套不上去。
为此笔者还换了好多方案,比如用射线检测向量,透视扭曲,平面法线,再到最后改用正交相机,都以失败告终,导致笔者一度陷入绝望状态。不过正交相机下条件比较简单,笔者还是发现了个规律:深度偏移量跟camera的zoom成正比。
zoom也会缩放深度缓冲,这样子想,我们拿project的值来算视角是不是就可以的呢?有了这一灵感之后,笔者又屁颠屁颠地跑去看写得那篇不错的文章:
深度冲突--threejs(webgl)_polygonoffsetfactor-CSDN博客
m: 表示最大深度斜率(Maximum Depth Slope)的值,是一个根据当前渲染的多边形相对于视线的角度自动计算出来的值。它基本上表示该多边形表面有多倾斜;如果表面与视线平行,则m值小,如果表面近乎垂直于视线,则m值大。
factor: 这是一个你可以控制的变量,对应于Three.js中的material.polygonOffsetFactor。这个数值会乘以上述的m值,也就是说,它表示深度偏移量将随着多边形的视觉倾斜程度而增加。
r: 这是指解析度,表示深度缓冲区每个单位的更改所能表示的最小深度差异。不同的系统和深度缓冲区的配置可能具有不同的解析度。
units: 同样是一个你可以控制的数值,对应于Three.js中的material.polygonOffsetUnits。这个数值会乘以r,提供了一个恒定的深度偏移,这个偏移与多边形的倾斜无关。
————————————————版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/weixin_45705239/article/details/138075785
这里写的是最大深度斜率,这么想,我们拿平面跟屏幕的夹角似乎就可以了,并且基于project(camera)的结果。因为project出来的z就是深度。
这里提一个高中立体几何的概念:二面角。笔者直接拿网上找来的一张图贴到这里。
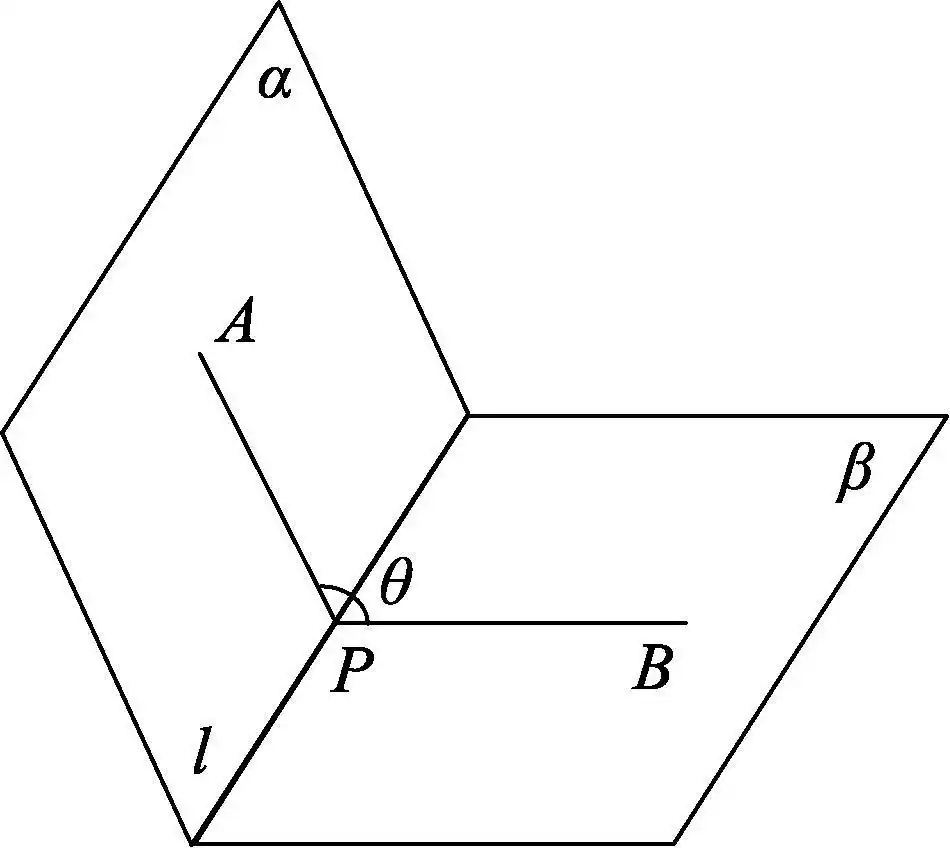
其中θ值代表α和β两平面的夹角(平面角),AP和AB均垂直于交线l。当然了,实际计算中,拿两平面的法线求点乘即可。
笔者用一个更简单的案例(跟上篇差不多)来试验,求深度斜率会更方便。
<!DOCTYPE html>
<html><head><meta charset="UTF-8"><title>three_polygonOffset</title><style>body {margin: 0;overflow: hidden;}</style><script src="three.js-master/build/three.js"></script><script src="three.js-master/examples/js/libs/dat.gui.min.js"></script>
</head><body><script>var scene = new THREE.Scene();var geometry = new THREE.PlaneGeometry(100, 100);var loader = new THREE.TextureLoader();var map = loader.load("three.js-master/examples/textures/UV_Grid_Sm.jpg")var srcColor = 0xFFFFFF;var material = new THREE.MeshBasicMaterial({ color: srcColor, map: map});var mesh = new THREE.Mesh(geometry, material);material.polygonOffset = true;material.polygonOffsetFactor = 0;material.polygonOffsetUnits = 0;mesh.rotation.y = Math.PI / 6;scene.add(mesh);var geometry2 = new THREE.PlaneGeometry(100, 100);var srcColor2 = 0xEEDDCC;var material2 = new THREE.MeshBasicMaterial({ color: srcColor2, map: null });var mesh2 = new THREE.Mesh(geometry2, material2);mesh2.rotation.y = Math.PI * 0;scene.add(mesh2);var width = window.innerWidth;var height = window.innerHeight;var scale = 4;// var camera = new THREE.OrthographicCamera(-width * 0.5 / scale, width * 0.5 / scale, height * 0.5 / scale, -height * 0.5 / scale, 0.1, 20000);var camera = new THREE.PerspectiveCamera(90, width / height, 0.1, 20000);camera.position.set(0, 0, 100);var renderer = new THREE.WebGLRenderer();renderer.setSize(width, height);renderer.setClearColor(0x000000, 1);document.body.appendChild(renderer.domElement);var gui = new dat.GUI(),folderCamera = gui.addFolder("相机"),propsCamera = {get '裁剪'() {return camera.near;},set '裁剪'(v) {camera.near = v;camera.updateProjectionMatrix();},};folderCamera.add(propsCamera, '裁剪', 0.01, 0.1);folderCamera.open();var folderPolygonOffset = gui.addFolder("polygonOffset");var propsPolygonOffset = {get 'polygonOffsetFactor'() {return material.polygonOffsetFactor;},set 'polygonOffsetFactor'(v) {material.polygonOffsetFactor = v;},get 'polygonOffsetUnits'() {return material.polygonOffsetUnits;},set 'polygonOffsetUnits'(v) {material.polygonOffsetUnits = v;},}folderPolygonOffset.add(propsPolygonOffset, 'polygonOffsetFactor', -500, 500);folderPolygonOffset.add(propsPolygonOffset, 'polygonOffsetUnits', -20000, 20000);folderPolygonOffset.open();function render() {renderer.render(scene, camera);requestAnimationFrame(render);}render();</script>
</body></html>本案例跟上篇差不多,不同的是设置polygonOffset的平面改成带旋转角度的那个,并且把水平面的网格去掉,观察起来要清晰一些。运行效果如下图所示。
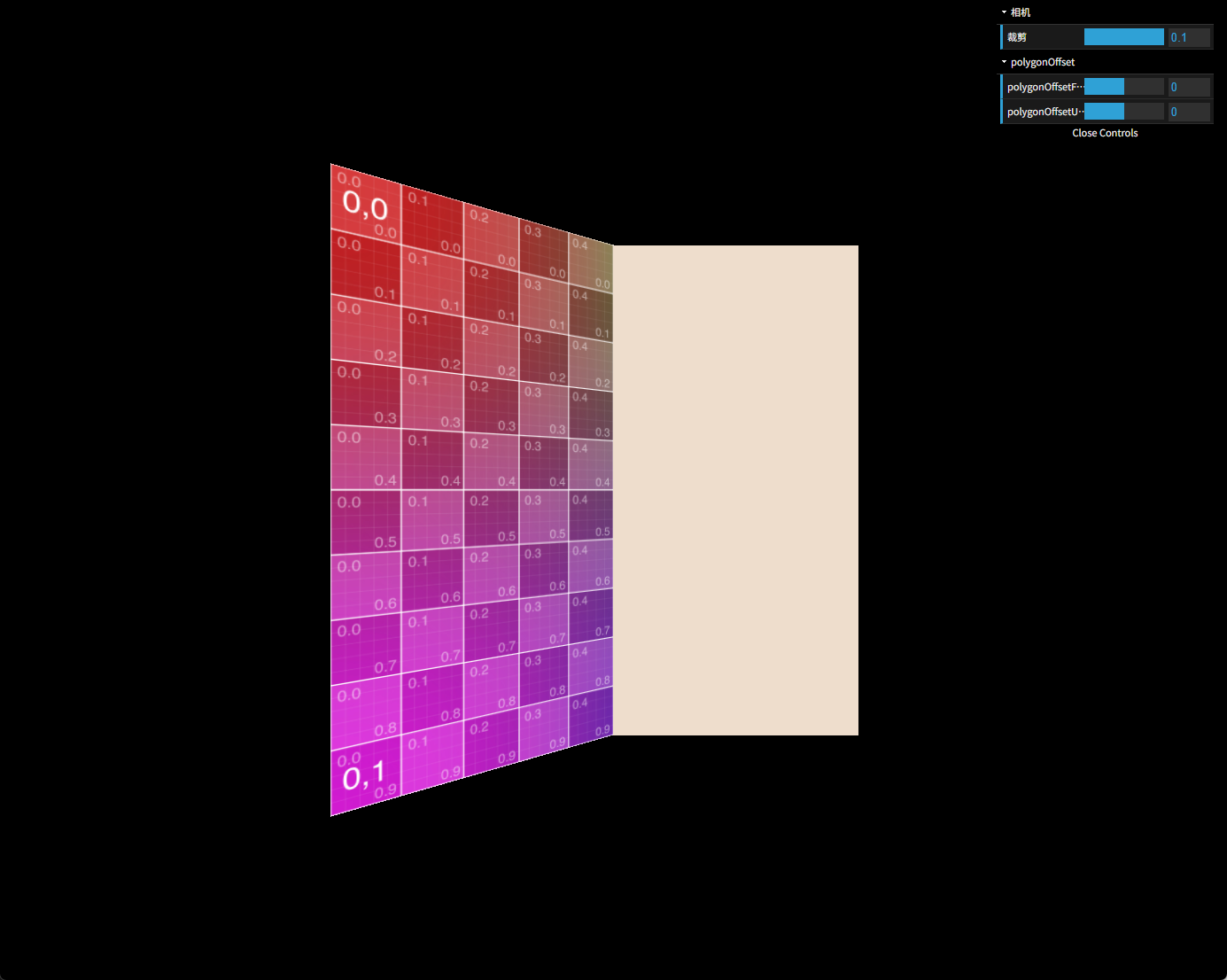
在平面绕y轴旋转了30度的情况下,polygonOffsetFactor调整为50,可以让两平面的交线对齐到网格线的第4条。
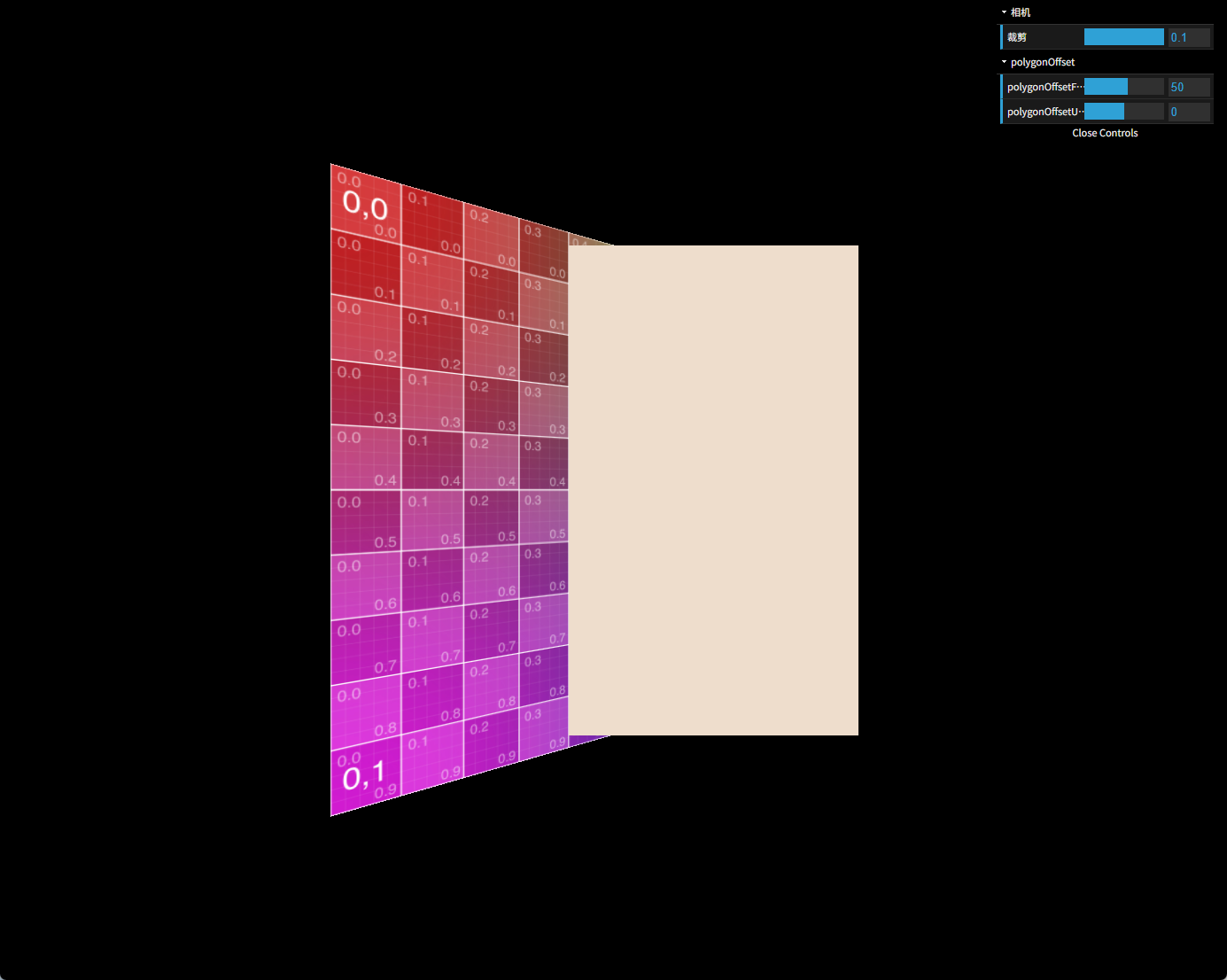
改到106则对齐到第3条网格线。
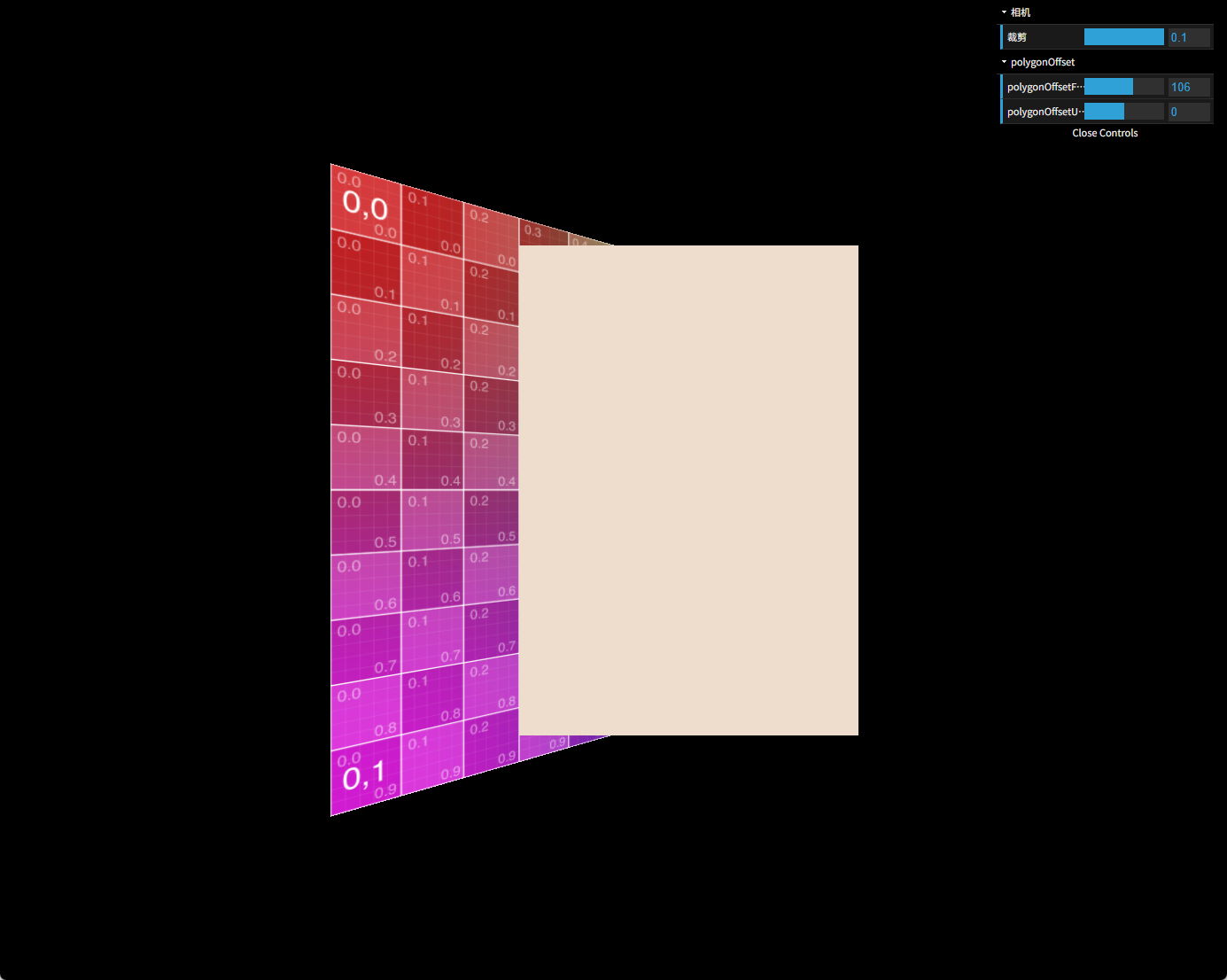
在研究polygonOffsetUnits的系数r时,我们已经验证到了偏移量的线性效果,所以本篇不会在固定的一个视角下做一张表来探讨polygonOffsetUnits的线性关系,毕竟本篇的重点是视角变量。
跟上篇类似,我们把第4条网格线的中点和第5条网格线的中点的project(camera)结果输出到控制台。

这样,我们就可以得出polygonOffsetFactor等于50时深度的偏移值为
0.9980099900499501-0.9979047263657369=0.00010526368421315269
也就是说,每一点factor为深度值带来的偏移量为
0.00010526368421315269/50=0.0000021052736842630535
然后重点来了,最大深度斜率的计算。由于我们要用project的结果来算,所以直接拿法线算不准确,因此还是用中学里的方法,找垂直于交线的直线进行求解。
对于本案例来说,我们直接拿上图中两个点的连线跟屏幕的夹角即可,因为那两个点的连线垂直于交线。深度斜率k具体的计算公式为
vec = (p2-p1)
k=vec.z/sqrt(vec.x^2+vec.y^2)
我们用到的点,y恒等于0,所以式子可以直接简化为
k=vec.z/vec.x。
好了,上控制台代码

也就是说,y旋转30度的平面在当前相机下的深度斜率k为。
现在我们理一下测试出来的结果。
一点factor的偏移量result=0.0000021052736842630535
深度斜率k=0.0014459929855301934
按照笔者引用的博文,m是根据k算出来的,我们姑且认为m跟k是一个线性关系,也就是m=c*k,c为一个我们待求的常量。
于是有result=m=c*k,c=result/k=0.0000021052736842630535/0.0014459929855301934=0.0014559363048992425
这是30度下的结果,我们把角度改成45度看看,可以改代码刷新,也可以控制台直接改
mesh.rotation.y = Math.PI / 4;
45度下,polygonOffsetFactor等于42可以让交线对齐到第4条网格线
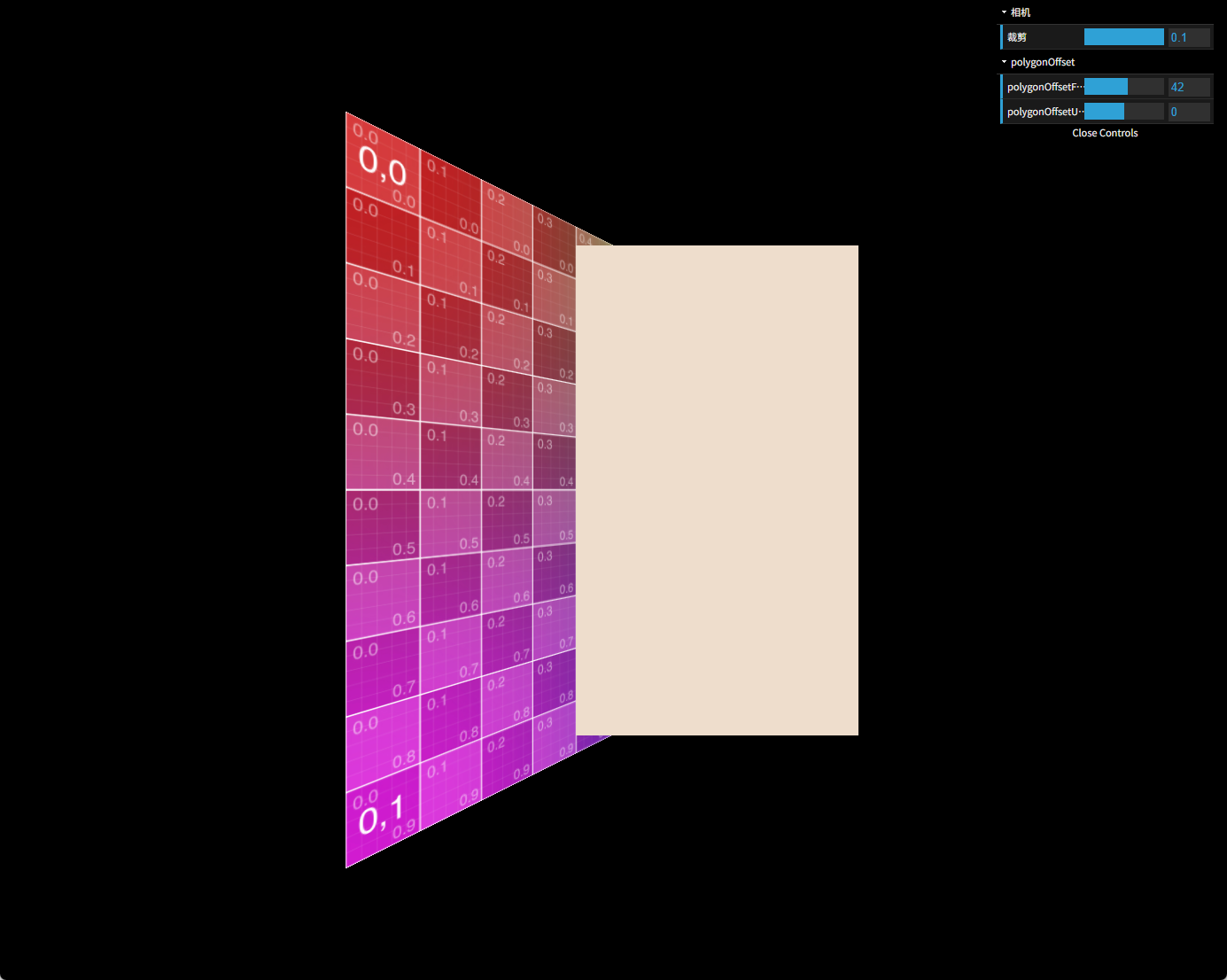

z偏移量为0.00015218302849029364,按前面的做法,result(单个factor带来的偏移值)=0.00015218302849029364/42=0.0000036234054402450866
然后深度斜率这样算:

于是有k=0.002504533318326064
c=result/k=0.0000036234054402450866/0.002504533318326064=0.0014467387651551926
不错,算出来的值跟30度时的相当接近。

虽然文字量不大(代码不算),但是篇幅也长了,所以60度的不再给出测试过程,直接上结果:
c=0.0014571165930502342
嗯,跟30度和45度也相等接近,但是这个数不像r那种2^-23那么的有计算机或者几何特征,所以笔者心里不踏实,就试着把camera.position.z设置为200再测一波。
比如这时候,60度得到的结果是0.0014391370784359598,也还接近,误差在可接受的范围内。
笔者怀疑自己的算深度斜率的方法不准确,然后在尝试着换不同的线来算夹角,比如试图接近千分之根号2,系数就显得不那么“魔术”。但不管怎么取,算出来的结果都在0.00144附近。
然后笔者还是不纠结了,就姑且拿这个魔术数作为结论,如果后面笔者发现这个魔术数的计算机或者几何特征,抑或找到了更准确的算法,笔者会第一时间通知大家。
本文算了一波,就得到一个魔术数0.00144,也不知道该如何小结了,那就把公式也汇总一下吧。
1 跟polygonOffsetFactor相关的系数m跟平面在当前相机下的最大深度斜率k有关,其值约等于0.00144*k
2 最大深度斜率k的值等于平面在相机下的旋转值跟屏幕所在平面的夹角的正切值,具体的计算方法是,找到跟平面交线垂直的直线,在其上取两点,分别算出project(camera)后,相减得到向量vec,用公式k=vec.z/sqrt(vec.x^2+vec.y^2)把k值算出来
3 跟屏幕绝对平行的平面,z值处处相等,所以vec.z恒等于0,k也就等于0,所以m=0.00144*k也等于0
4 结合上文,我们可以得到polygonOffset最终的计算公式,以24位深度缓冲为例,深度偏移量的最终值等于
其中vec是平面跟屏幕交线垂直的一根直线的向量。
有了这样的量化公式后,我们调整polygonOffset两个参数时,就有了很好的理论指导,不用再老是盲猜了。
理论有点抽象,笔者在考虑要不要再来一篇博文,通过例子说明该如何根据这个公式计算业务场景中的入参数值。如果再来,就再发一篇9.3,否则就开启新的主题,进入10或者10.1。
看这么多,想必大家多少有点晕了,而笔者也是时候歇一下,嗯大家先好好消化消化,辛苦大家了。










)

)


深入了解AVFoundation-编辑:视频变速功能-实战在Demo中实现视频变速)
|实战指南:构建论文分析智能体)


