B. Meeting on the Line

题目：

思路：

数形结合

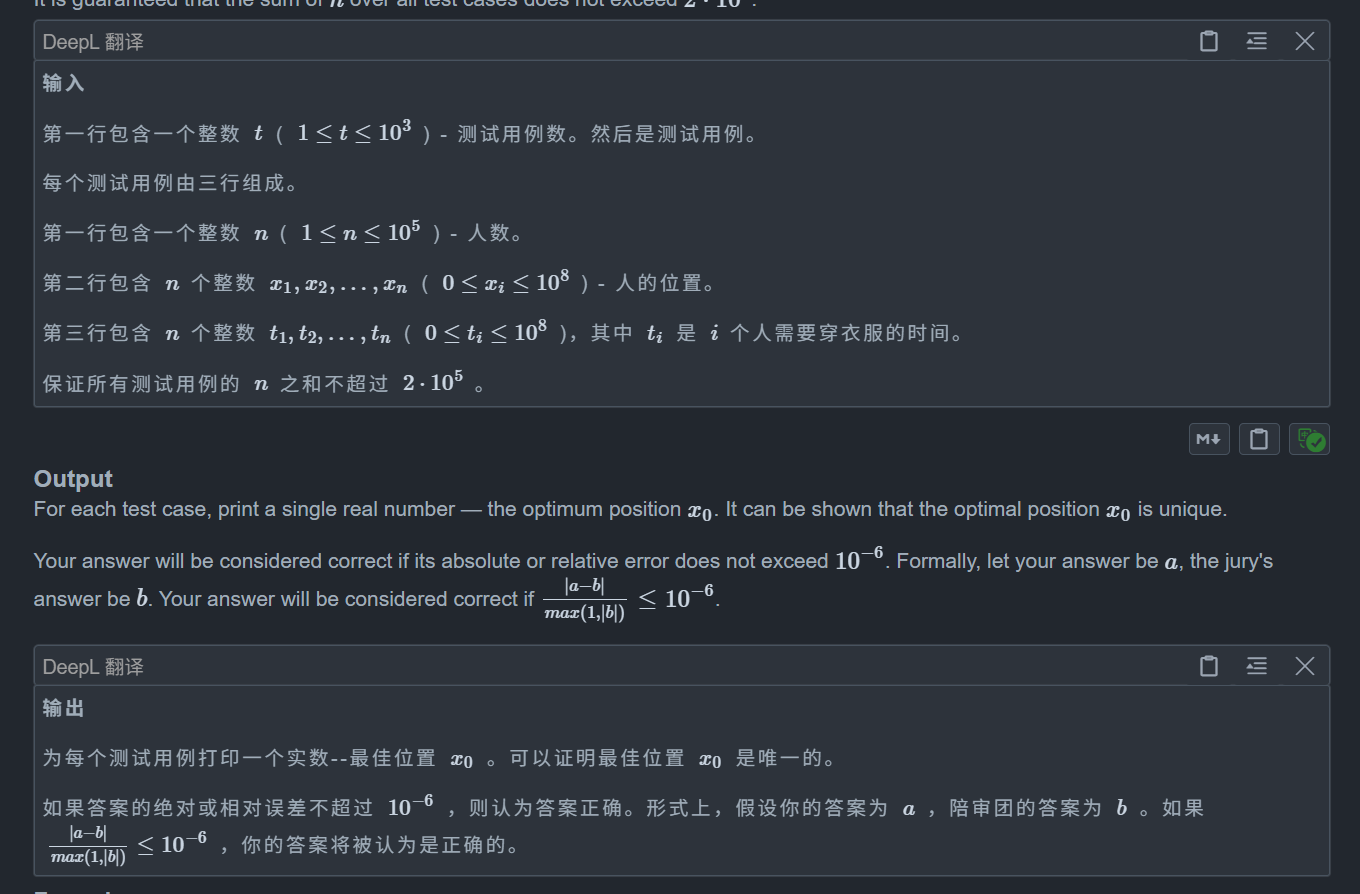
首先考虑如果没有 t 的影响该怎么写

显然我们就是让最大时间最小化，那么显然选择最左端点和最右端点的中间值即可，即 (mi + mx) / 2，那么现在有了 t 该怎么办

我们不妨考虑拆开绝对值，由 |a - b| = max(a-b, b-a) 可得原式 t - |x - x0| 拆解为

max(t - (x - x0), t - (x0 - x)) = max(t - x + x0, t + x - x0) = max(x0 - (x - t), (t + x) - x0)

我们令 x-t 和 t+x 为两个新点，那么显然 x-t 在 x0 左边，t+x 在 x0 右边，所以我们找到最大的右端点和最小的左端点即可，这就是我们上面的普通情况

除此之外，我们可以还能使用二分or三分

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n;cin >> n;vector<int> a(n + 1), t(n + 1);for (int i = 1; i <= n; i++)cin >> a[i];for (int i = 1; i <= n; i++)cin >> t[i];int mx = -1e18, mi = 1e18;for (int i = 1; i <= n; i++){mx = max(mx, a[i] + t[i]);mi = min(mi, a[i] - t[i]);}double res = (mx + mi) * 1.0 / 2.0;printf("%.6lf\n", res);
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

---

C1. Sheikh (Easy version)

题目：

思路：

异或性质

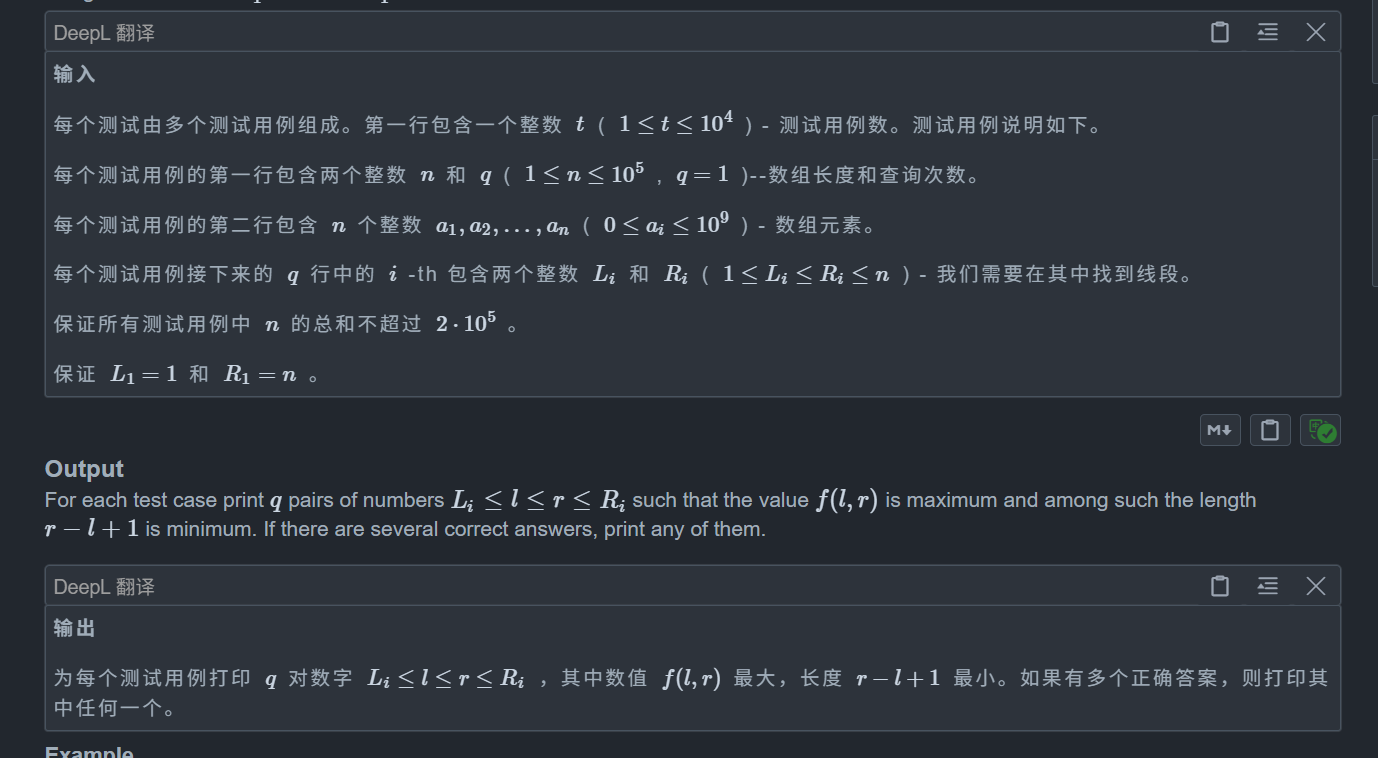
这题看似无从下手，但是我们关键点在于发现异或的性质，不难发现一个特点，异或是不带进位的加法，那么对于任意 x,y，我们都有 x+y >= x ^ y，这是显然的

那么我们就豁然开朗了，既然 x+y >= x ^ y，那么对于一个区间我们肯定是多加数的，因为 x+y - x^y >= 0 恒成立，所以多加显然是不劣的

那么最大值显然就是选取整个区间，但是题目让我们输出最小的长度，所以考虑如何最小

显然由上诉结论可知，我们区间长度越长，那么值就越大，这是单调的，所以我们考虑二分区间长度，我们枚举每一个左端点，然后二分最大长度即可

特别注意预处理前缀和即可，还有越界问题

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n,q;cin >> n >> q;vector<int> a(n+1),sum(n+1,0),sumxor(n+1,0);for (int i = 1; i <= n; i++){cin >> a[i];sum[i] = sum[i-1] + a[i];sumxor[i] = sumxor[i-1] ^ a[i];}cin >> q >> q;int mx = sum[n] - sumxor[n];auto check = [&](int l,int len)->int{int r = min(l + len - 1,n);int nmx = (sum[r] - sum[l-1]) - (sumxor[r] ^ sumxor[l-1]);return nmx >= mx;};int le = 1e18;int mxl = 0;for (int i = 1; i <= n; i++){int l = 1,r = 1e18;while (l+1 < r){int mid = l+r >> 1;if(check(i,mid)){r = mid;}else{l = mid;}}int templen = 0;if(check(i,l)) templen = l;else templen = r;if(templen < le){le = templen;mxl = i;}}cout << mxl << " " << mxl + le - 1 << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

---

E. Guess the Cycle Size

题目：

思路：

随机数据的特征

注意到题目数据随机，那么可以考虑稍微暴力的做法

我们假设对于 a,b 点对进行询问，如果 a,b 和 b,a 的询问结果不同，那么显然二者相加就是答案

但是由于 a,b 和 b,a 的询问结果不同，因此我们要多次判断，可以发现 50 次内基本上不可能会错，如果担心错的话可以在代码结尾加上 while(1) 使得其超时，因为TLE 会重测 3 次，3 次全错肯定不可能

最后特别注意特判 -1 情况即可

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int ans1, ans2;for (int i = 2; i <= 1e18; i++){cout << "? " << 1 << " " << i << endl;cin >> ans1;if (ans1 == -1){cout << "! " << i - 1 << endl;return;}cout << "? " << i << " " << 1 << endl;cin >> ans2;       if(ans1 != ans2){cout << "! " << ans1 + ans2 << endl;return;} }while (1);
}signed main()
{int t = 1;while (t--){solve();}return 0;
}