【菜狗每日记录】启发式算法、傅里叶变换、AC-DTC、Xmeans

🐱1、启发式算法

① 定义

② 特点

③ 案例

🐱2、快速傅里叶变换FFT

① DFT离散傅里叶变换

② FFT快速傅里叶变换

🐱3、AC-DTC聚类

🐱4、Xmeans

🐱1、启发式算法

启发式算法是和最优化算法相对的。

一般而言，最优化算法所需要解决的问题，都能分成三个部分：

目标：什么是目标呢？简单点说就是要优化的东西，比如运筹学的背包问题中，要优化的就是所选物品的价值，使其最大。
决策：顾名思义就是根据目标所作出的决策，比如在这里就是决定选取哪些物品装进我们的背包。
约束：那么何又为约束呢？就是说再进行决策时必须遵循的条件，比如上面的背包问题，我们所选取的物品总的重量不能超过背包的容量。要是没有容量的约束，小学生才做选择呢，我全都要！

在求最优解过程中，启发式策略可依个体或全局经验调整搜索路径，当求最优解困难时，它是高效得可行解的方法。这种算法主要用于解决NP-hard问题，NP即非确定性多项式。

① 定义

基于直观、经验构造的算法，在一定成本下给出可以解决优化问题的一个可行解。主要以仿自然算法为主。

遗传算法，模拟退火，各种群算法，蚁群，鱼群，粒子群，人工神经网络等模仿自然界或生命体行为模式的算法，一般又称人工智能算法或全局优化算法。

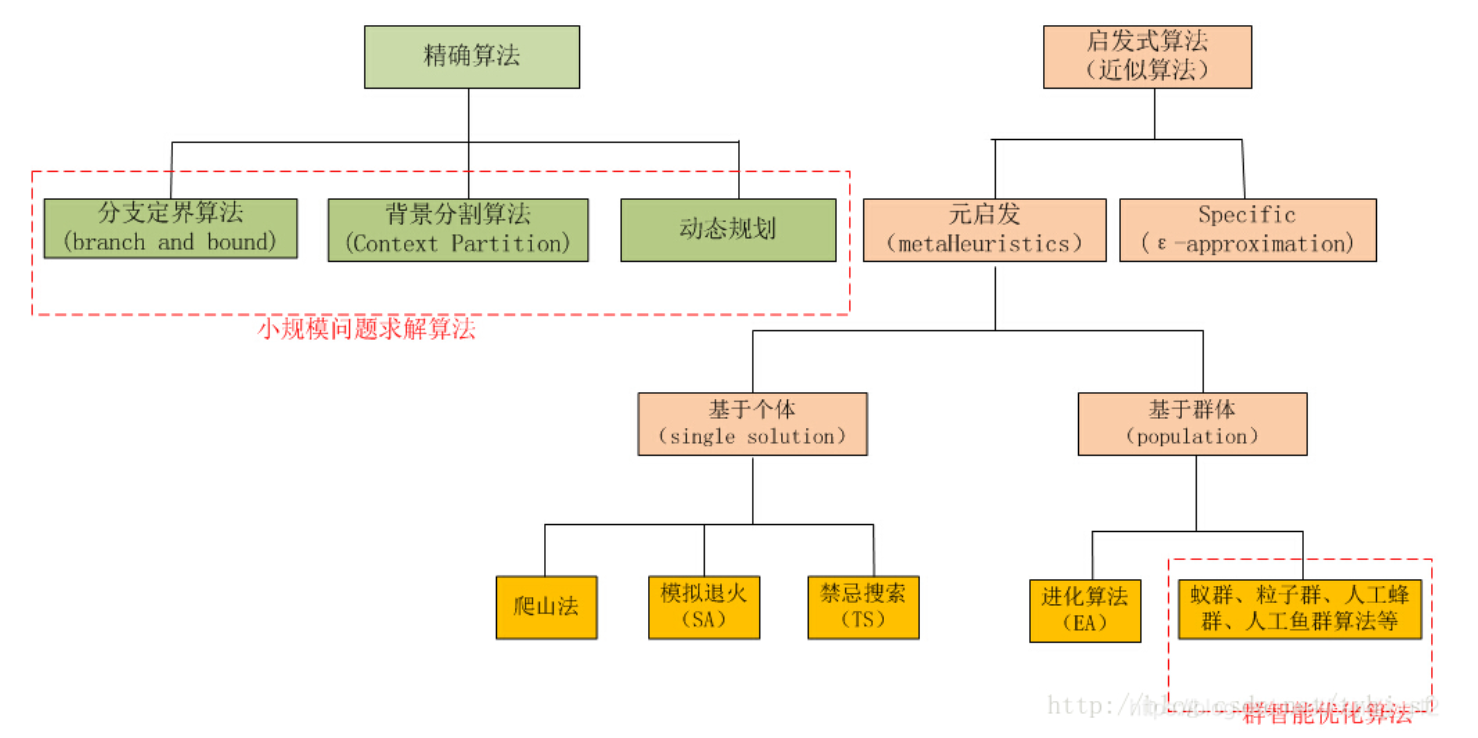
② 特点

帮助寻求答案，告诉怎么去找，知道路怎么走，不知道路往哪里走。
结果具有偶然性，过程具有启发性，像是问路的过程中了解更多目的地相关的内容。（这里感觉很像人生，一直在路上，不断寻找自己想要追求的。）

③ 案例

通俗理解启发式算法 - 知乎

最终目标：爬上最高的山峰。

爬山法：一个人往更高的地方走，会变更高，但是那座山不一定是珠穆朗玛峰。
模拟退火：一个人喝醉了，随机跳了很长时间，可能变高可能变低，但是慢慢朝更高的地方走。
禁忌搜索：很多人，互相转告哪个地方的山已经去了，留下一个人做记号，制定了下一步往哪里找的策略。
遗传算法：人活在地球，不知道自己要干什么，过几年就会杀死低海拔的土地上的人，人们也会自己去找最高的山峰。

🐱2、快速傅里叶变换FFT

① DFT离散傅里叶变换

        对于任意多项式系数表示转点值表示，可以随便取任意n个x值代入计算,但这样时间复杂度是O ( n 2 )所以伟大数学家傅里叶取了一些特殊的点代入，从而进行优化。
        他规定了点值表示中的n个x为n个模长为1的复数。这n个复数不是随机的，而是单位根。
        把上述的n个复数（单位根）ω n0 , ω n1 . . . . . , ωn−1代入多项式，能得到一种特殊的点值表示，这种点值表示就叫DFT（离散傅里叶变换）。

想象你有一个多项式，比如，通常我们用它的系数（这里是1、2、1）来表示它。但另一种方法是，你可以找一些点，比如，然后算出这些点对应的的值，分别是1、4、9。这样，你就可以用这三个点（0,1）、（1,4）、（2,9）来表示这个多项式。这种方法就叫点值表示。

复数可以看成是平面上的点，有实部和虚部。模长就是这个点到原点的距离。如果一个复数的模长为1，那就意味着它在平面上离原点的距离正好是1。这些点都落在一个以原点为中心、半径为1的圆上，这个圆叫单位圆。

现在，我们要在单位圆上均匀地找n个点。比如，n=4，我们就在单位圆上找4个等分的点。这些点在数学里叫单位根。它们有一个很特别的性质：当你把它们代入多项式的时候，计算会变得很方便。

所以，这句话的意思是：在点值表示法中，我们选择的n个x值，不是随便挑的，而是单位圆上的n个均匀分布的点。这些点都是模长为1的复数，它们在计算多项式的时候特别有用。

② FFT快速傅里叶变换

虽然DFT能把多项式转换成点值但它仍然是暴力代入n nn个数，复杂度仍然是O(n2)，所以它只是快速傅里叶变换的朴素版。

原始信号：一首复杂的交响乐

想象你听到一首交响乐，里面有：

🎻 小提琴（高音）、🎺 小号（中音）、大鼓（低音等等各种乐器同时演奏

你的耳朵听到的是混合在一起的复杂声音。

FFT就像"音乐分析师"

FFT的作用就是：戴上专业耳机：把混合的音乐分解开，分析频谱：告诉你这首曲子里有：

30%的小提琴声（高频）

25%的小号声（中频）

45%的鼓声（低频）

概念	通俗解释	在您研究中的应用
FFT	音乐分解器	把驾驶动作分解成不同频率成分
重采样	重新编曲	把长短不一的驾驶片段变成统一长度
保持特征	保留原曲风格	加速还是加速，减速还是减速

一句话总结：FFT就像给每个驾驶片段做"DNA分析"，找出它的本质特征，然后根据这个特征重新生成标准长度的片段，方便后续比较和分析。

🐱3、AC-DTC聚类

聚类分为两个不同的类别:分层聚类（从很多类到几个类）和分区聚类（从一个类切分到很多类）。

其中分层聚类使用：相似性递归聚类——构建树形图探索不同粒度级别的聚类。

AC-DTC的层次特性有效地捕获了行动阶段数据中的时间依赖性和变化，促进了相似行动阶段的准确聚类，同时反映了细微的差异

DTC（Dynamic Tree Cutting，动态树切） 是整个算法的关键部分。它的核心作用是：在层次聚类（得到一棵树状图 dendrogram）之后，自动决定如何切割树来得到合理的簇数，而不是人工设定某一个“水平线”来切。

它是层次聚类（Hierarchical clustering）的一种后处理策略：层次聚类（AC）会生成一棵树状图（dendrogram），从“每个点单独一类”到“所有点合并成一类”的整个过程都能看到。但层次聚类本身不会告诉你“在哪一层切开”才是最佳聚类结果。

动态树切分（DTC）就是自动分析这棵树的结构，根据数据的上下文，灵活决定在哪里剪枝，把数据划分成更合适的簇。

AC：自底向上合并，先一个点一类，然后逐步合并。

DTC：对生成的树图进行动态切分，得到最终聚类。

合起来，AC-DTC 能：

自动调整簇的数量（不像普通层次聚类需要手动定层次）。
更好地处理“动作阶段数据”这种长度不一、内部有细节差异的序列。

四种 linkage 方法（ward, average, complete, weighted）指的是在聚类分析中，用于计算样本点之间距离或相似度的四种不同的连接方式。下面分别解释一下这四种方法：

ward：Ward方法是一种基于方差分析的方法。它通过最小化类内方差来确定簇，目的是使得每个簇内的样本点尽可能紧密地聚集在一起。在每次合并簇时，会选择使得总方差增加最小的簇对进行合并。这种方法适用于球形簇，并且对簇的大小较为敏感，簇大小差异较大时可能会影响聚类效果。
average：平均连接法（也称为UPGMA，Unweighted Pair Group Method with Arithmetic mean）。它计算两个簇中所有样本点对之间的平均距离，作为这两个簇之间的距离。这种方法相对较为稳健，不会因为簇中个别异常点而对簇间距离产生过大影响，适用于不同形状和大小的簇。
complete：最大连接法（也称为Furthest Neighbor）。它以两个簇中所有样本点对之间的最大距离作为这两个簇之间的距离。这种方法对异常值较为敏感，因为簇间距离由最远的点对决定，可能会导致一些较小的簇被过早地合并，适用于簇形状较为规则的情况。
weighted：加权平均连接法（也称为WPGMA，Weighted Pair Group Method with Arithmetic mean）。它在计算簇间距离时，会考虑簇的大小，对簇中样本点的数量进行加权。这种方法在一定程度上平衡了簇的大小对簇间距离的影响，适用于簇大小差异较大的情况，能够更合理地反映簇之间的相似性。