一个很有意思的dfs模拟题_前序遍历

这个问题的话前置内容显然是字典序,什么是字典序呢?
顾名思义,就是词语在字典中的顺序,也就是我们最常说的a,abandon,ability(我记得前三个是这个)
这是一种字符串之间比较大小的常用策略,即:从前到后,一个个比较字符,如果分出大小了,就按照这个结果作为字符串大小比较的结果。
如果此时一个字符串已经没有字符了(遍历完了),就算这个字符串更小。举个例子,abcd和acb,谁会在字典前面出现呢?显然是abcd,哪怕他更长,但是在第二个字符的时候就已经比出来结果了。
好了,现在明确了字典序,那么其实我们对于这个题目的意思其实也就明白了,虽然我的解题方法确实没有用到字典树,但是我觉得这确实是一个很直观的方式:

灵魂画手哈哈
但是表达的意思其实还是比较明确了的,这个树说明的是在第一个数字是1的情况下的,我们后续所有可能的数字,第二行就表示第二个数字为0-9的各种情况,然后一层层下去。
这意味着每一个节点都表示一个数字,并且一路遍历最左边节点得到的数字都一定是当前字典序最小的数字。
所以我们只需要使用一个方式, 按照字典序最小的情况来遍历这个树不就可以了。
解题过程
这个方式实际上并不难想,就是DFS深度优先遍历,这可以让我们从最上面的根节点开始,每一次都走到当前可以走的不重复的最左边的节点(回去的步骤不算的话)
另外,头结点这里,我画的是1,但是实际上1-9都是可以的,这里不能在上面再加一层的原因是,如果要加的话,这个头只能是0,但是这样我们最后还是需要把他去除掉。
复杂度
- 时间复杂度: O(n)
- 空间复杂度: O(1)
class Solution {
public:
vector<int> ans;
void dfs(int num,int n){
if(num>n){
return;
}
ans.push_back(num);
for(int j=0;j<10;j++){
dfs(num*10+j,n);
}
}
vector<int> lexicalOrder(int n) {
for(int i=1;i<=9;i++){
dfs(i,n);
}
return ans;
}
};
模拟: 标记 实现*删除
class Solution {
public:
string clearStars(string s) {
int n = s.size();
// 记录每种字母的出现位置
vector<int> vec[26];
// 记录删除哪些位置的字母
bool ban[n];
memset(ban, 0, sizeof(ban));
for (int i = 0; i < n; i++)
{
if (s[i] == '*')
{
// 通过枚举找到最小字母
for (int c = 0; c < 26; c++) if (vec[c].size() > 0)
{
// 删除最靠右的该字母
ban[vec[c].back()] = true;
vec[c].pop_back();
break;
}
} else {
// 字母,记录出现位置
vec[s[i] - 'a'].push_back(i);
}
}
// 构造答案
string ans;
for (int i = 0; i < n; i++) if (s[i] != '*' && !ban[i]) ans.push_back(s[i]);
return ans;
}
};
os七层:
物 数 网 传 会 表 应
矩阵和求原矩阵 lc1605
- 贪心:每一步取最小
- 可以横着填
class Solution {
public:
vector<vector<int>> restoreMatrix(vector<int>& rowSum, vector<int>& colSum)
{
int m=rowSum.size(),
n=colSum.size();
vector<vector<int>> ret(m,vector<int>(n,0));
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
ret[i][j]=min(rowSum[i],colSum[j]);
rowSum[i]-=ret[i][j];
colSum[j]-=ret[i][j];
}
}
return ret;
}
};
分区起止位置标记
class Solution {
public:
vector<int> partitionLabels(string s) {
unordered_map<char, int> lastPos;
// 记录每个字符最后出现的位置
int n = s.size();
for (int i = 0; i < n; ++i) {
lastPos[s[i]] = i;
}
vector<int> ret;
int start = 0;
int end = 0;
for (int i = 0; i < n; ++i)
{ //遍历字符串
end = max(end, lastPos[s[i]]); // 更新
if (i == end)
{ // 到达终点
ret.push_back(end - start + 1);
start = i + 1; // 下一个起点
}
}
return ret;
}
};
奇偶 不另开两队列
+2 实现ret的方法
class Solution {
public:
vector<int> rearrangeArray(vector<int>& nums) {
int n = nums.size();
int i = 0, j = 1;
vector<int> ret(n);
for (int num : nums) {
if (num > 0) {
ret[i] = num;
i += 2;
} else {
ret[j] = num;
j += 2;
}
}
return ret;
}
};
股票的资本损益
select
stock_name,
sum(case when operation='buy' then -price else price end ) as 'capital_gain_loss'
from
Stocks
group by
stock_name
从股票交易表(Stocks)里,按股票名称分组统计买卖后的资金盈亏。
- 核心逻辑:
- 遇到买入操作(buy),用 -price 表示资金减少(花钱买股票);
- 遇到卖出或其他操作,用 +price 表示资金增加(卖股票赚钱);
- 最后把同一只股票的所有操作金额相加(sum),得出这只股票的总盈亏(capital_gain_loss)。
举例:
若某股票买入2次(价格100、200),卖出1次(价格300),
计算为: -100 -200 +300 = 0 ,即不赚不亏。
C++ 的 explicit 关键字用于禁止构造函数的隐式类型转换
- 没有 explicit 时:若构造函数只有一个参数,编译器会自动用该参数创建对象(隐式转换)。
例: int a = 1; MyClass obj = a; (假设 MyClass 有 MyClass(int) 构造函数,会隐式用 a 创建 obj )。
- 加上 explicit 后:禁止这种隐式转换,必须显式创建对象。
例: MyClass obj(a); (必须用括号明确调用构造函数)。
作用:避免意外的类型转换,让代码意图更清晰,减少潜在 bug。
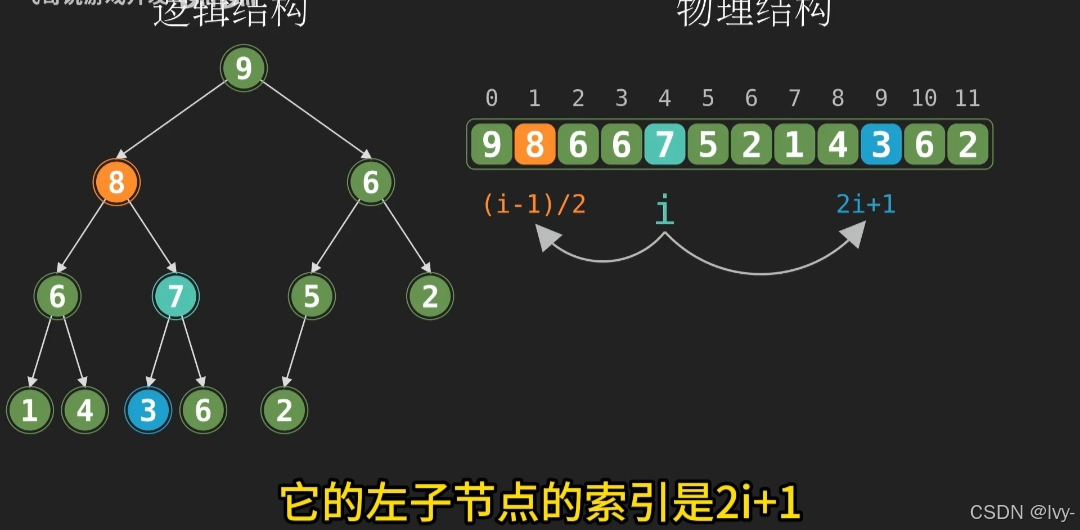
heap的实现



二分查找

递归转动态规划

cpu vs gpu


![2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)](http://pic.xiahunao.cn/2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答))




)



,已实现python、C#)

: 使用DeepSeek指导Qwen强化学习)






结合稀缺数据预测婴儿脑连接|文献速递-深度学习医疗AI最新文献)