概述

计算OpenGL的正交投影矩阵和透视投影矩阵是有现成函数的。自己手推不是为了重复造轮子。手推一遍，可以极大的加强对这两个矩阵的理解。同时也可以满足一下自己求知欲。

正交投影矩阵手推

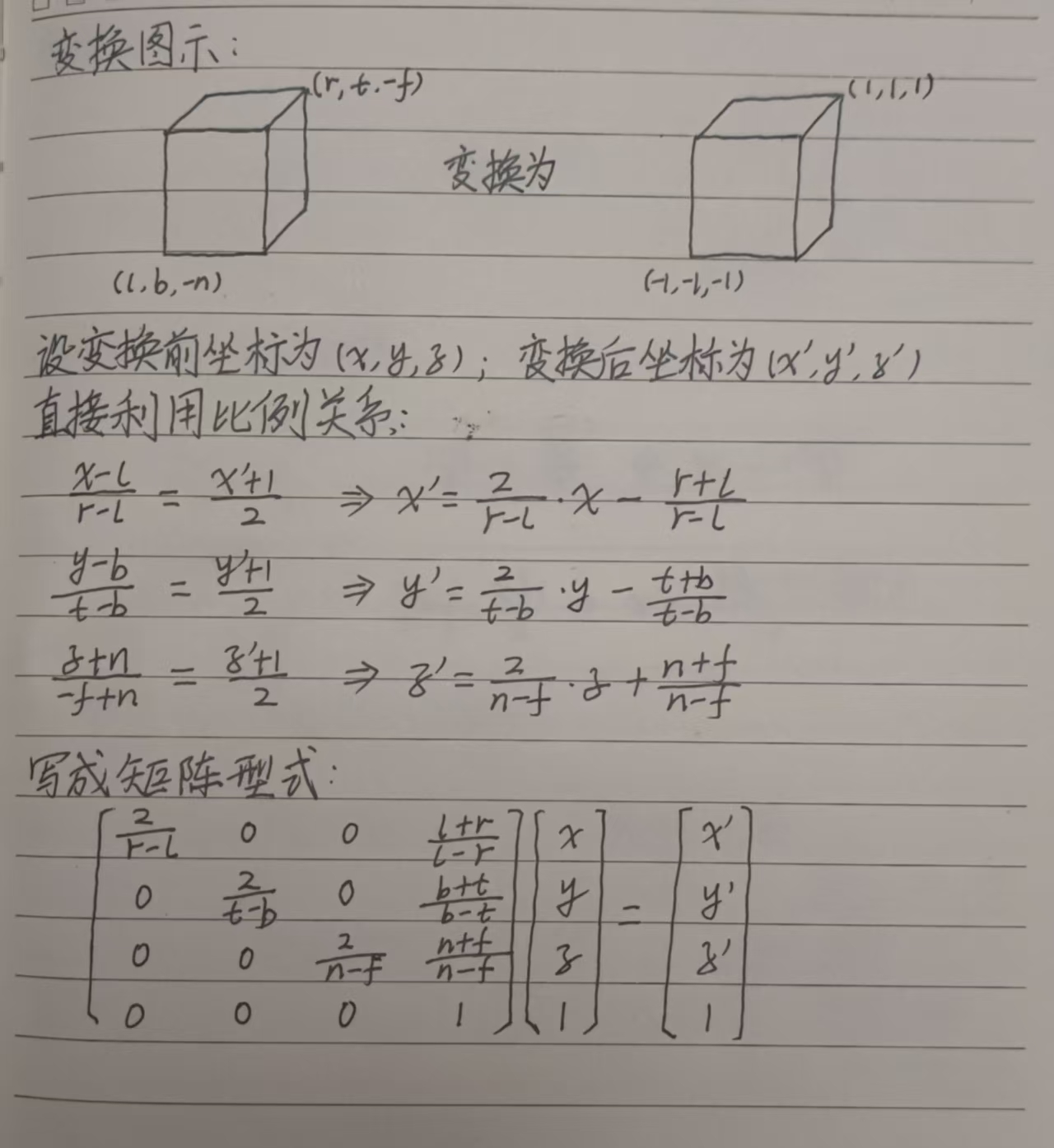
正交投影矩阵源码

WGMatrix4x4 WGMatrix4x4::BuildOrtho(double l, double r, double b, double t, double n, double f) {WGMatrix4x4 matrix;double w = r - l;double h = t - b;double d = f - n;matrix.m_elements[0][0] = 2 / w;matrix.m_elements[0][1] = 0;matrix.m_elements[0][2] = 0;matrix.m_elements[0][3] = -(r + l) / w;matrix.m_elements[1][0] = 0;matrix.m_elements[1][1] = 2 / h;matrix.m_elements[1][2] = 0;matrix.m_elements[1][3] = -(t + b) / h;matrix.m_elements[2][0] = 0;matrix.m_elements[2][1] = 0;matrix.m_elements[2][2] = -2 / d;matrix.m_elements[2][3] = -(f + n) / d;matrix.m_elements[3][0] = 0;matrix.m_elements[3][1] = 0;matrix.m_elements[3][2] = 0;matrix.m_elements[3][3] = 1;matrix.m_type = WGMatrix4x4Type::TRS;return matrix;
}

透视投影矩阵手推

透视投影矩阵源码

WGMatrix4x4 WGMatrix4x4::BuildFrustum(double l, double r, double b, double t, double n, double f) {WGMatrix4x4 matrix;double w = r - l;double h = t - b;double d = f - n;matrix.m_elements[0][0] = 2 * n / w;matrix.m_elements[0][1] = 0;matrix.m_elements[0][2] = (r + l) / w;matrix.m_elements[0][3] = 0;matrix.m_elements[1][0] = 0;matrix.m_elements[1][1] = 2 * n / h;matrix.m_elements[1][2] = (t + b) / h;matrix.m_elements[1][3] = 0;matrix.m_elements[2][0] = 0;matrix.m_elements[2][1] = 0;matrix.m_elements[2][2] = -(f + n) / d;matrix.m_elements[2][3] = -2 * f * n / d;matrix.m_elements[3][0] = 0;matrix.m_elements[3][1] = 0;matrix.m_elements[3][2] = -1;matrix.m_elements[3][3] = 0;matrix.m_type = WGMatrix4x4Type::Unknown;return matrix;
}