简单来说,在回归问题中,最常用的损失函数是均方误差(MSE, Mean Squared Error)和平均绝对误差(MAE, Mean Absolute Error)。它们衡量的都是模型预测值(ŷ)与真实值(y)之间的“距离”或“差异”。
下面我来详细解释它们的意思、区别和用途。
1. 均方误差 (MSE) - L2 Loss是什么意思?
均方误差是回归问题中最常见、最基础的损失函数。它的计算方法是:
- 1.先计算每一个数据点的预测值与真实值的差(误差)。
- 2.将这个差平方(所以叫“均方”)。
- 3.将所有数据点的平方误差加起来,再求平均。
数学公式:
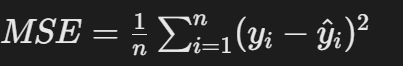
其中:
n是样本数量。- yi是第
i个样本的真实值。 - y^i是模型对第
i个样本的预测值。
直观理解与特点:
- 放大大的误差:因为误差被平方了,所以如果一个预测误差很大(例如误差为10,平方后变成100),它会比多个小误差(例如多个误差为1,平方后还是1)对总损失的贡献大得多。
- 曲线光滑:数学性质很好,便于求导(它的导数是一个线性函数),这使得在梯度下降等优化算法中非常高效。
- 对异常值敏感:这是它的一个主要缺点。如果数据中存在少数偏离很大的异常值,MSE会变得非常大,模型会为了拟合这些异常值而牺牲对整体数据的拟合效果。
用途:广泛应用于各种回归问题,是很多模型的默认损失函数。
2. 平均绝对误差 (MAE) - L1 Loss是什么意思?
平均绝对误差的计算方法是:
- 1.计算每一个数据点的预测值与真实值的差的绝对值。
- 2.将所有绝对误差加起来,再求平均。
数学公式:

直观理解与特点:
- 线性惩罚误差:无论误差是1还是10,它对总损失的贡献就是1和10,是线性的关系。不会特别放大大的误差。
- 对异常值更鲁棒:正因为它是线性惩罚,所以个别异常值不会像在MSE中那样对损失产生巨大的影响,模型不会轻易被异常值“带偏”。
- 曲线不光滑:在零点处不可导(导数突然从-1变为+1),这在优化时可能不如ME高效(但在实际中可以通过次梯度等方法解决)。
用途:当你认为数据中含有异常值,并且不希望模型过度关注这些异常点时,MAE是一个很好的选择。
对比与总结
特性 | 均方误差 (MSE) | 平均绝对误差 (MAE) |
|---|---|---|
计算方式 | 误差的平方的平均 | 误差的绝对值的平均 |
对异常值 | 敏感 | 不敏感(更鲁棒) |
梯度性质 | 光滑,易于优化 | 在零点不可导,优化稍复杂 |
解读 | 惩罚大的误差非常严厉 | 对所有误差一视同仁 |
另一个重要的损失函数:Huber Loss
你可能会问,有没有一个损失函数能结合MSE和MAE的优点呢?答案是有的,这就是 Huber Loss。
Huber Loss 是一个混合损失函数。它在一个阈值 δ(delta)范围内,它的行为像MSE(曲线光滑,易于优化);当误差超过这个阈值时,它的行为像MAE(对大的异常值更鲁棒)。
特点:
- best of both worlds:兼具MSE的优化友好和MAE的异常值鲁棒性。
- 需要超参数:你需要手动设置一个阈值 δ。
用途:当数据中明显存在异常值,但你又不愿意完全使用MAE时,Huber Loss是一个非常出色的折中方案。
总结
- 分类问题的核心是预测概率分布,所以用交叉熵来衡量两个分布之间的差异。
- 回归问题的核心是预测一个连续值,所以用基于距离的损失函数(如MSE, MAE)来衡量预测值与真实值的差距。
- MSE是最常用的,数学性质好,但对异常值敏感。
- MAE对异常值不敏感,但优化起来稍麻烦。
- Huber Loss是一个聪明的结合体,在很多情况下能提供更好的性能。
选择哪个损失函数取决于你的数据、模型和你最关心什么。通常可以从MSE开始,如果发现模型效果受异常值影响很大,再尝试MAE或Huber Loss。
)


)




)



))





通信)
处理)