基于Master-Slave主从博弈论的储能与能源协调算法matlab仿真

1.课题概述

2.系统仿真结果

3.核心程序

4.系统仿真参数

5.系统原理简介

6.参考文献

7.完整工程文件

1.课题概述

基于Master-Slave主从博弈论的储能与能源协调算法matlab仿真.主从博弈（Stackelberg Game）是一种具有层级决策结构的博弈模型，包含主导者（Leader）和跟随者（Follower）两类主体。在储能与能源协调场景中，微网运营商（MGO）作为主导者，率先制定电价、热价等策略；用户聚合商（用户侧）作为跟随者，根据主导者策略动态调整自身的用电、用热及储能使用策略，最终通过反向归纳法求解双方策略的均衡点，实现系统整体效益最大化。

2.系统仿真结果

3.核心程序

matlab2024b

.................................
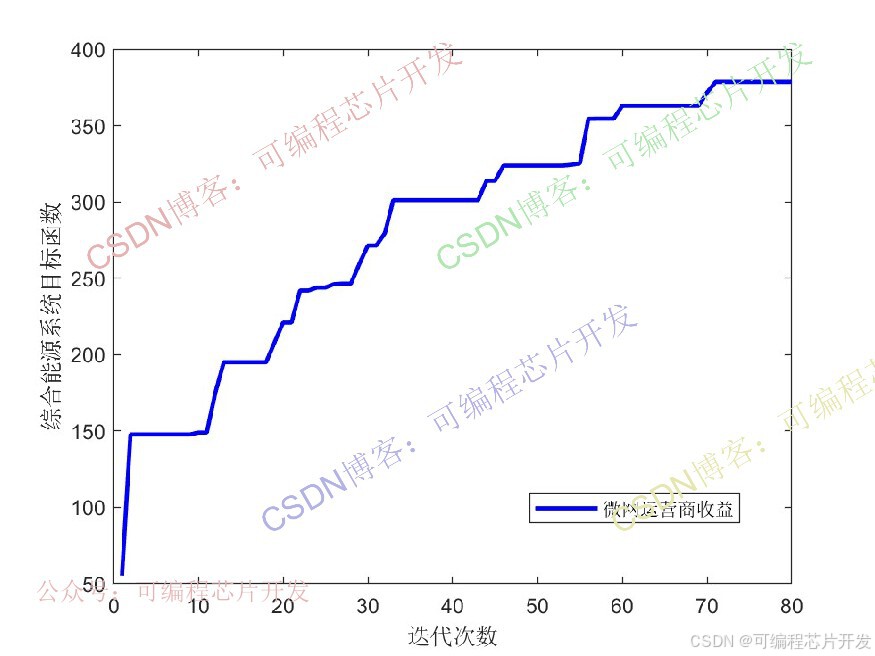
figure
plot(yy1,'b','linewidth',2)
hold on
xlabel('迭代次数');
ylabel('综合能源系统目标函数');
legend('微网运营商收益')xx=1:Tm;
PP=value([H_buy;Prl]);
figure
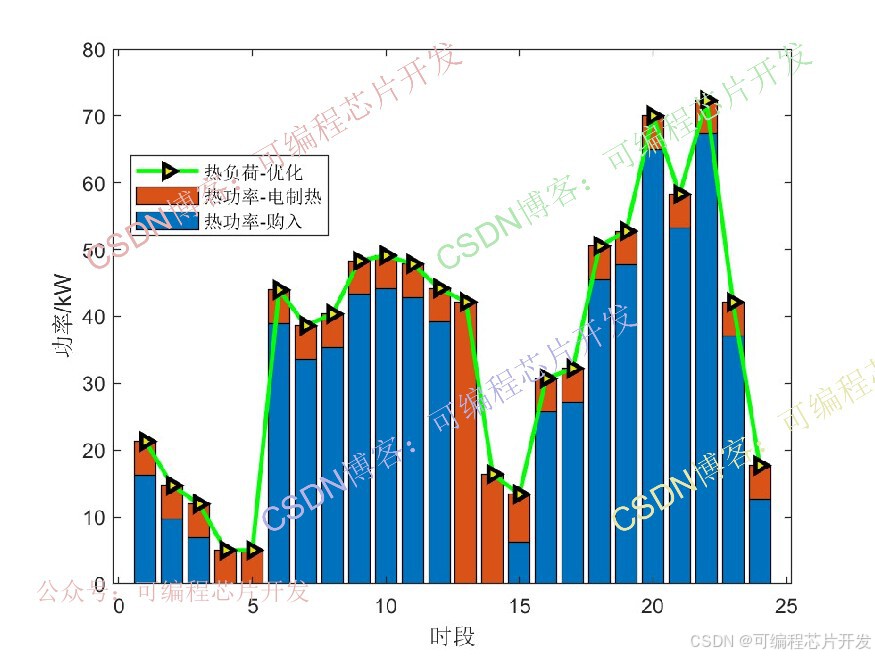
bar(PP',0.8,'stack');
hold on
plot(value(H_buy+Prl),'-g>',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);legend('热功率-购入','热功率-电制热','热负荷-优化');
xlabel('时段');
ylabel('功率/kW');figure
subplot(311);
bar(PV_pw,'g')
hold on
plot(E_load,'-mo',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.5,0.9,0.0]);hold on
plot(H_load,'-r^',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.2,0.9,0.5]);hold on
xlabel('时间/h');
ylabel('曲线/kW');
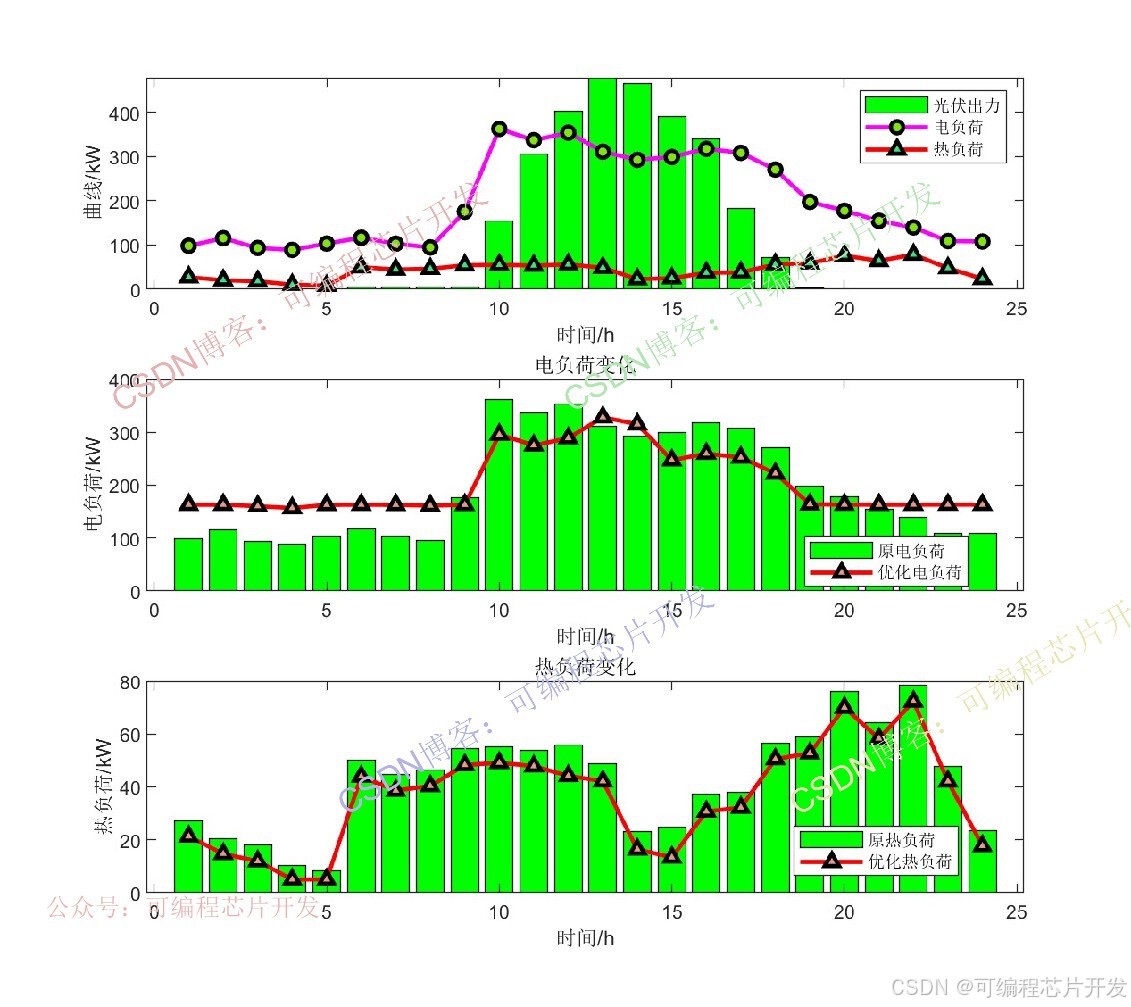
legend('光伏出力','电负荷','热负荷');subplot(312);
bar(E_load,'g');
hold on
plot(Eall_load,'-r^',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.6,0.5]);hold on 
xlabel('时间/h');
ylabel('电负荷/kW');
title('电负荷变化');
legend('原电负荷','优化电负荷');subplot(313);
bar(H_load,'g');
hold on
plot(Hall_load,'-r^',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.6,0.5]);
hold on 
xlabel('时间/h');
ylabel('热负荷/kW');
title('热负荷变化');
legend('原热负荷','优化热负荷');figure
subplot(211);
xx=1:Tm;
stairs(Prices,'g','linewidth',2);
hold on
stairs(Priceb,'b','linewidth',2);
hold on
stairs(ybest(1,xx),'r-o','linewidth',1);
xlabel('时间/h');
ylabel('电价/元');
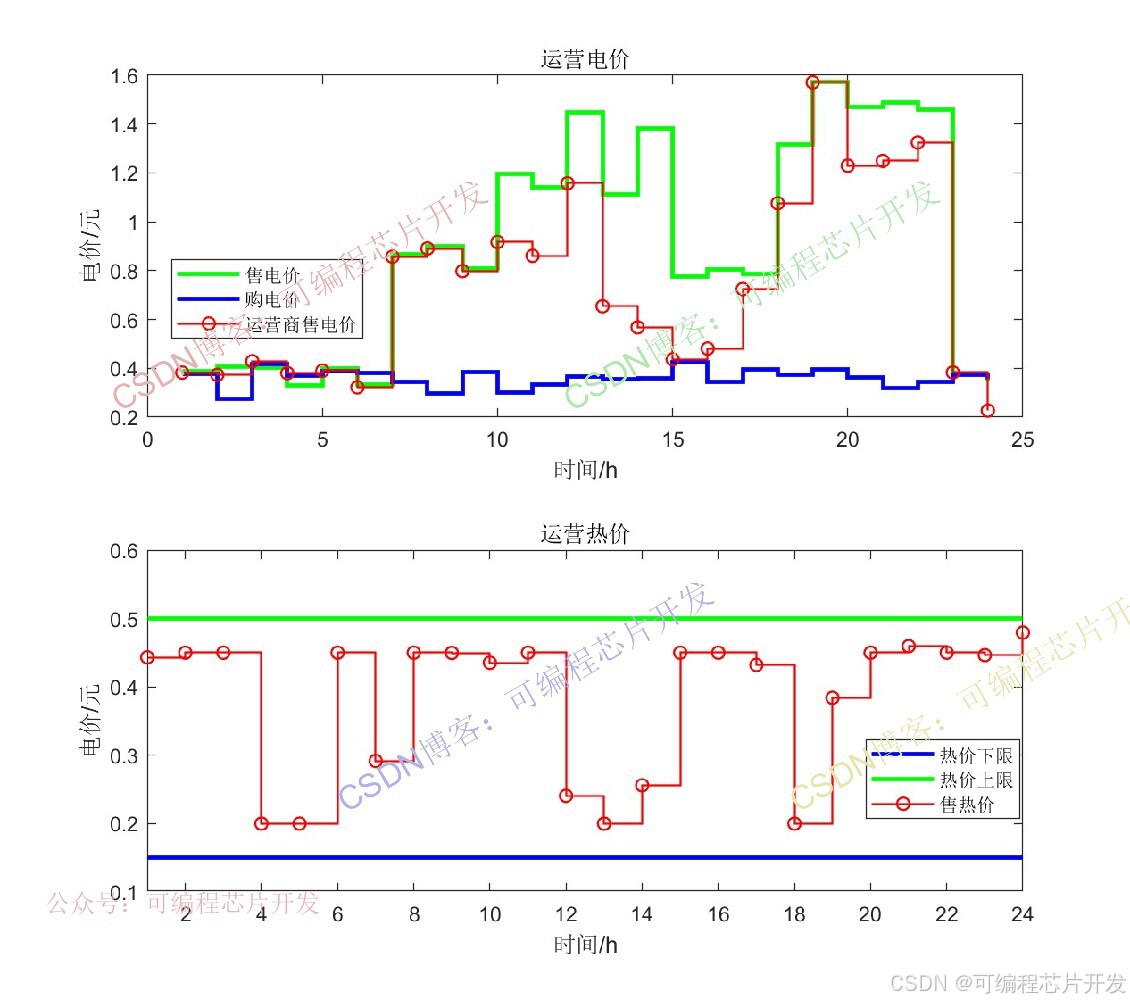
title('运营电价');
legend('售电价','购电价','运营商售电价');subplot(212);
xx=1:Tm;
stairs(Hmin,'b','linewidth',2);
hold on
stairs(Hmax,'g','linewidth',2);
hold on
stairs(ybest(1,xx+Tm),'r-o','linewidth',1);
xlabel('时间/h');
ylabel('电价/元');
title('运营热价');
axis([1,Tm,0.1,0.6]);
legend('热价下限','热价上限','售热价');
114

4.系统仿真参数

%主从博弈优化过程
%差分进化算法参数初始化
Pr   = 0.5;           % 变异缩放因子 
Pc   = 0.9;           % 交叉概率 %种群参数设置
Nums = 25;    % 种群规模 
dims = 48;    % 个体维度（前24维为电价，后24维为热价）
Iters= 80;   % 最大迭代次数（控制算法运行周期）

5.系统原理简介

决策目标：最大化自身收益，包含与电网的电力交易收益、向用户售电售热收益，同时最小化燃气轮机运行成本。

微网运营商侧：

用户聚合商侧：

将用户聚合商的最优反应策略代入微网运营商模型，求解其收益最大化问题：

目标函数：最大化微网运营商收益

通过遗传算法更新电价与热价策略，具体操作包括：

选择：基于轮盘赌选择策略，保留高收益策略。

交叉：以交叉概率（如 80%）生成新策略组合。

变异：以变异概率（如 5%）随机调整策略参数。

该算法通过主从博弈框架实现了微网运营商与用户聚合商的策略协同，结合共享储能与电制热等灵活资源，有效提升了系统整体效益。未来可扩展方向包括：

多主体博弈：引入共享储能运营商作为独立博弈方，优化其服务费定价策略；

不确定性建模：考虑光伏出力、负荷需求的随机性，采用随机规划或鲁棒优化；

实时调度：结合模型预测控制（MPC），将日前优化扩展至日内滚动优化。

6.参考文献

[1] 董朝阳，赵俊华，文福拴，等。从智能电网到能源互联网：基本概念与研究框架 [J]. 电力系统自动化，2014,38 (15):1-11.
[2] 孙宏斌，郭庆来，潘昭光。能源互联网：理念、架构与前沿展望 [J]. 电力系统自动化，2015,39 (19):1-8.
[3] 丁涛，牟晨璐，别朝红，等。能源互联网及其优化运行研究现状综述 [J]. 中国电机工程学报，2018,38 (15):4318-4328+4632.
[4]MOHSENIAN-RAD H. Coordinated price-maker operation of large energy storage units in nodal energy markets[J]. IEEE Trans on Power Systems,2016,31(1):786-797.