目录
1.递归实现归并排序的思想及图解
2.递归实现归并排序的代码逻辑
2.1嵌套子函数
2.2递归过程
2.3递归结束条件
2.4归并及拷贝过程
3.非递归实现归并排序的思想及图解
4.非递归实现归并排序的代码逻辑
4.1边归并边拷贝
4.2某一gap下归并完成才进行拷贝
5.归并排序的时间复杂度与空间复杂度
以升序为例
1.递归实现归并排序的思想及图解
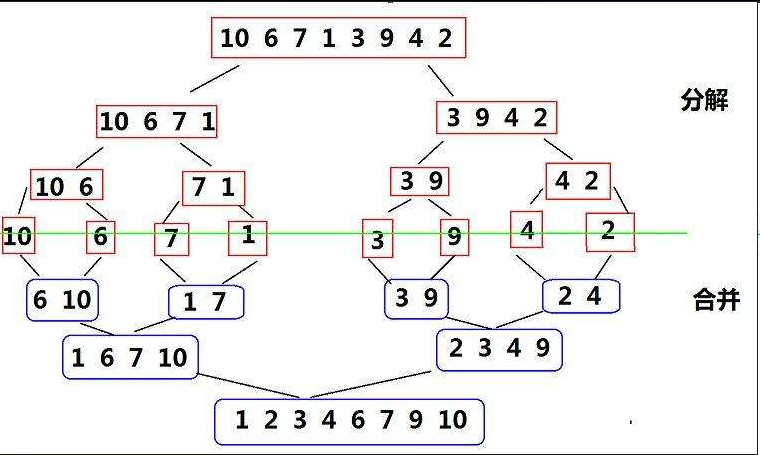
两两数组有序,借助一个临时数组就可将有序两数组合并成一个新的有序数组,这就叫归并
对于给定的待排序数组,我们运用递归策略,不断地将其对半拆分,直到被拆分的子数组只有一个元素时(此时认为子数组有序),我们开始进行归并操作,......最终使数组有序
2.递归实现归并排序的代码逻辑
2.1嵌套子函数
为了避免递归频繁创造临时数组而造成空间消耗,此时需要嵌套子函数
void _MergeSort(int* a, int left, int right, int* tmp);
void MergeSort(int* a, int n);void MergeSort(int* a, int n){int* tmp = (int*)malloc(sizeof(int) * n);if (!tmp){perror("malloc fail");return;}//对[0, n - 1]这段区间进行排序_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}归并排序的递归操作类似于二叉树的后序遍历(左子树、右子树、根)
因为只有当原数组的两部分数组都有序后,才能通过归并使整个数组有序
void _MergeSort(int* a, int left, int right, int* tmp)
{//结束条件//递归过程//归并区间//归并到临时数组的对应位置//拷贝}2.2递归过程
递归过程类似于后序遍历
int midi = left + (right - left) / 2;
//[left, midi][midi + 1, right]
_MergeSort(a, left, midi, tmp);
_MergeSort(a, midi + 1, right, tmp);
//开始归并此时中间值midi的取法是向下取整,且具有防溢出的特性,使得 left <= midi < right
所以,终止条件 left >= right 合乎情理
标准的左右区间的划分[left, midi][midi + 1, right]
使子区间不重叠,递归范围严格缩小,合并时覆盖了整个区间
当数组只有两个数,下标从0到1并进行递归划分时,midi = 0,
此时左区间[left, midi] 递归可以停止,右区间同理
int mid = left + (right - left + 1) / 2; // 向上取整
//[left, midi - 1][midi, right]mergeSort(arr, left, mid - 1); // 左子区间mergeSort(arr, mid, right); // 右子区间
//开始归并向上取整有风险
此时区间需要做调整
当数组只有两个数,下标从0到1并进行递归划分时,midi = 1,
此时左区间如果是[left, midi] 将造成无限递归,所以更改为[left, midi - 1][midi, right]
2.3递归结束条件
根据思想,我们可以知道区间长度等于1时就停止递归,那么
//结束条件 if (left >= right)return;且向下取整得到 midi 的做法使得 left 不会大于 right
2.4归并及拷贝过程
以升序为例
递归返回后区间所对应的数组就有序了,此时就可以进行归并操作
1.先确定两有序数组的边界 begin. end.是对应数组的首元素下标、尾元素下标
2.从前往后顺次比较两有序数组,数组元素小的先放到临时数组中,一个数组结束后,再归并另一数组
3.图解
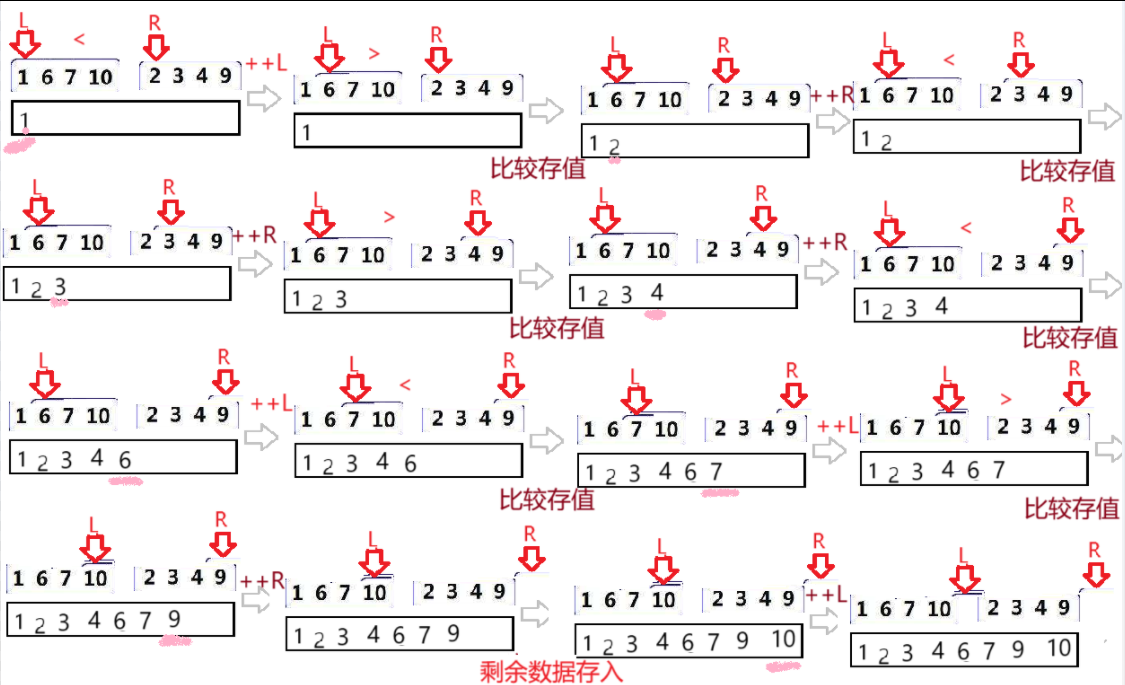
//开始归并
int begin1 = left, end1 = midi;
int begin2 = midi + 1, end2 = right;
//归并到临时数组的对应位置
int i = left;
while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[i++] = a[begin1++];else tmp[i++] = a[begin2++];
}while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];//拷贝
memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));归并区间不一定从0开始,而是从 left 开始的
两个begin下标都未到尾才继续比较存值,否则就跳出循环
此时常规思路就是是由if else语句判断到底哪一个begin下标未到尾然后再存值,
但上述做法直接利用while循环进行判断,这种做法更简洁
最后再将临时数组的归并内容拷贝会原数组,原数组对应位置就有序啦
通过递归使得数组最终都有序了
3.非递归实现归并排序的思想及图解
递归实现归并排序总是先递归到小规模数组,再从底层向上开始归并,即先是一个元素与一个元素进行归并,再是两个元素与两个元素进行归并.....这显然也可以是一种双重循环
外层循环是每组元素的个数,内存循环就是数组归并的过程

4.非递归实现归并排序的代码逻辑
4.1边归并边拷贝
(1)归并显然要借助临时数组
void MergeSortNonR1(int* a, int n)
{//临时数组int* tmp = (int*)malloc(sizeof(int) * n);if (!tmp){perror("malloc fail");return;}//归并过程free(tmp);tmp = NULL;
}(2)特定gap(确定的每组个数)下的归并过程
int gap;
for (int i = 0; i < n; i += 2 * gap){//表示区间int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2*gap - 1;//修正边界//开始归并int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[j++] = a[begin1++];else tmp[j++] = a[begin2++];}while (begin1 <= end1)tmp[j++] = a[begin1++];while (begin2 <= end2)tmp[j++] = a[begin2++];//边归并边拷贝memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}(3) 区间表示
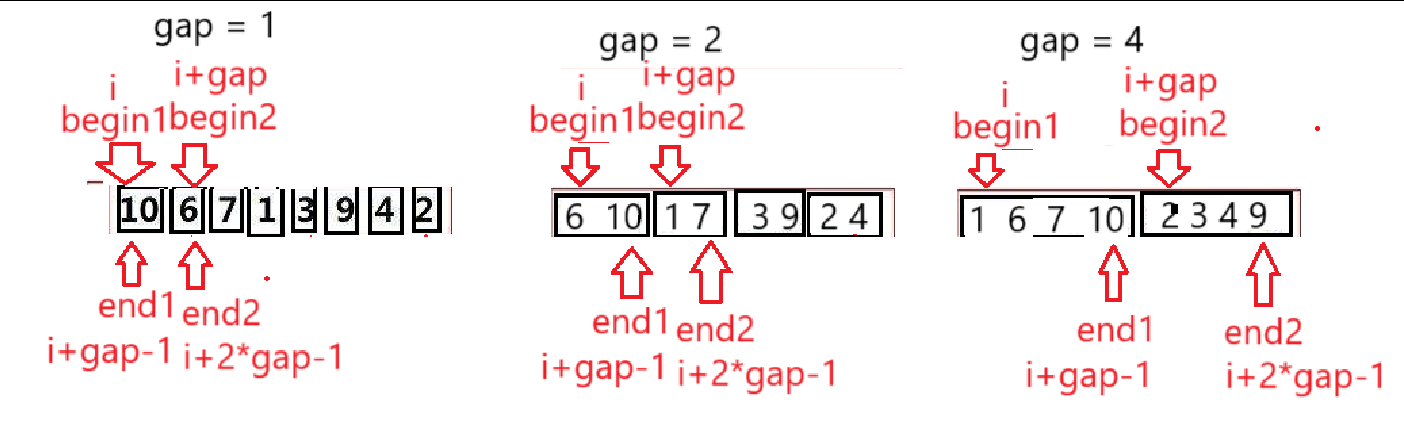
上述图解的gap与数组个数成倍数关系,万一有奇数个元素,是否会越界呢?
(4)修正边界
printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);打印确定gap下的区间帮助我们观察越界情况
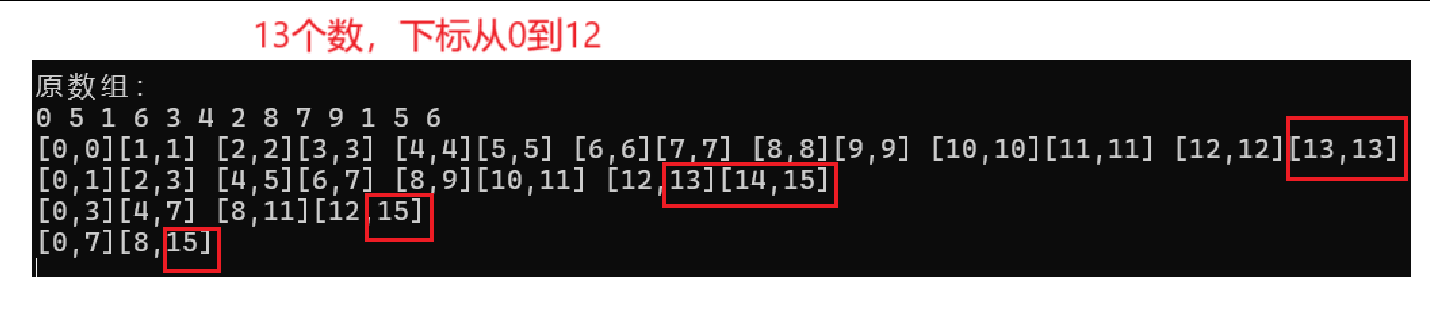
从打印结果来看,end1、begin2、end2都存在越界的可能
而for循环中的i控制了小于n的情况,所以begin1不存在越界访问的说法
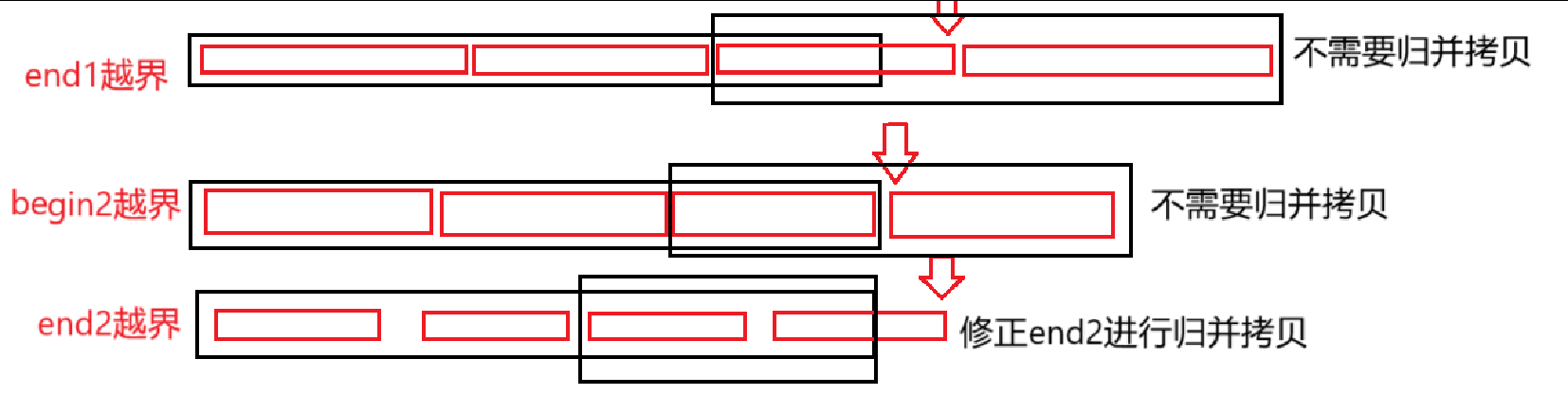
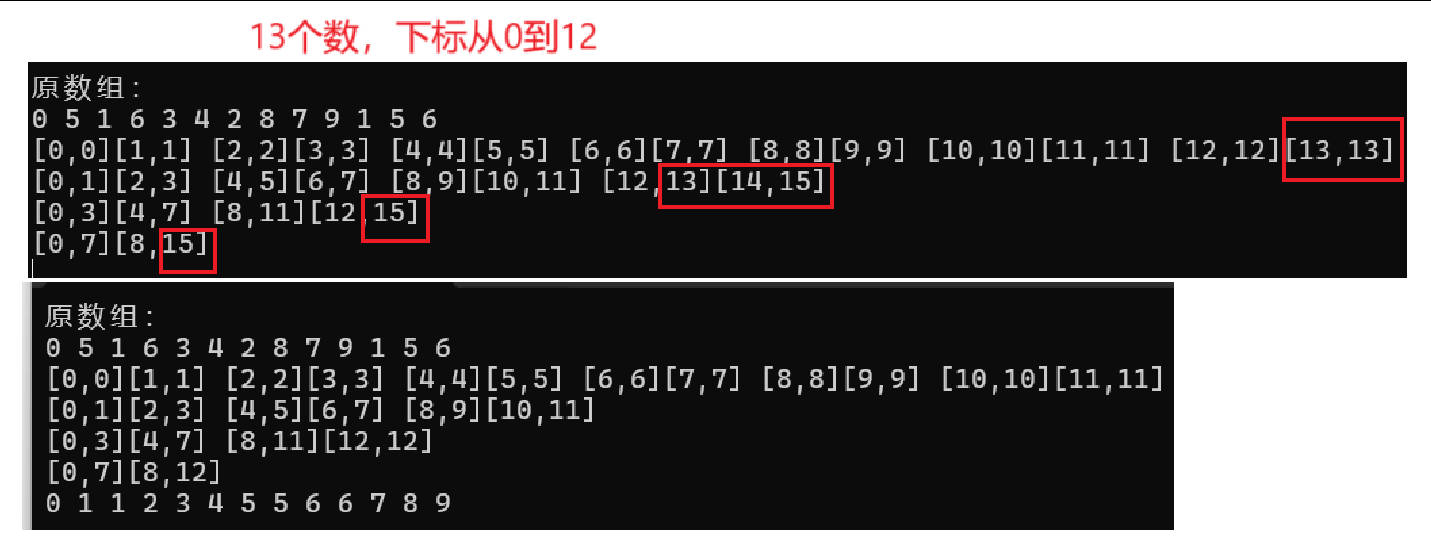
边归并边拷贝过程中,当end1越界之后,begin2、end2肯定也越界了,此时第一部分没有存入临时数组再拷贝回原数组的必要,而当begin2越界而end1没越界时,第一部分也不需要归并拷贝
//修正边界if (end1 >= n || begin2 >= n)break;else if (end2 >= n)end2 = n - 1;只有end2越界时,第二部分的部分需要与第一部分进行归并拷贝,此时将end2修正为 n - 1
再次打印边界,对比发现不合理的区间都已跳过
最后控制gap逐渐增大即可
void MergeSortNonR1(int* a, int n){int* tmp = (int*)malloc(sizeof(int) * n);if (!tmp){perror("malloc fail");return;}//每组中的个数int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){//表示区间int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2*gap - 1;//修正边界if (end1 >= n || begin2 >= n)break;else if (end2 >= n)end2 = n - 1;//查看边界越界情况需要//printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);//开始归并int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[j++] = a[begin1++];else tmp[j++] = a[begin2++];}while (begin1 <= end1)tmp[j++] = a[begin1++];while (begin2 <= end2)tmp[j++] = a[begin2++];//边归并边拷贝memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}//printf("\n");//查看边界越界情况需要gap *= 2;}free(tmp);tmp = NULL;
}
4.2某一gap下归并完成才进行拷贝
void MergeSortNonR2(int* a, int n){int* tmp = (int*)malloc(sizeof(int) * n);if (!tmp){perror("malloc fail");return;}//每组中的个数int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){//表示区间int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//修正边界//查看越界情况才需要printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);//开始归并int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[j++] = a[begin1++];else tmp[j++] = a[begin2++];while (begin1 <= end1)tmp[j++] = a[begin1++];while (begin2 <= end2)tmp[j++] = a[begin2++];}//查看越界情况才需要printf("\n");//全部归并完成后一次性拷贝memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp);tmp = NULL;
}打印边界

同样只有begin1不会越界,但是因为我们最终是将临时数组全部拷贝到原数组中去,所以
我们要确保不进行归并的部分也存入了临时数组,防止临时数组全部拷贝到原数组中去的过程中对原数据造成覆盖
if (end1 >= n)
{end1 = n - 1;begin2 = n;end2 = n - 1;
}
else if (begin2 >= n)
{begin2 = n;end2 = n - 1;
}
else if (end2 >= n)end2 = n - 1;end1越界要将end1修改为 n - 1,使得第一部分能够存入临时数组,并且将第二部分的区间改为不存在,即 begin2 > end2 ,这样才能避免第二部分的越界存值
end1未越界,begin2越界,此时将第二部分的区间改为不存在,即 begin2 > end2 ,避免第二部分的越界存值即可
只有end2越界,此时将其修改为 n - 1 即可,这样可以保证一二部分进行归并存值操作
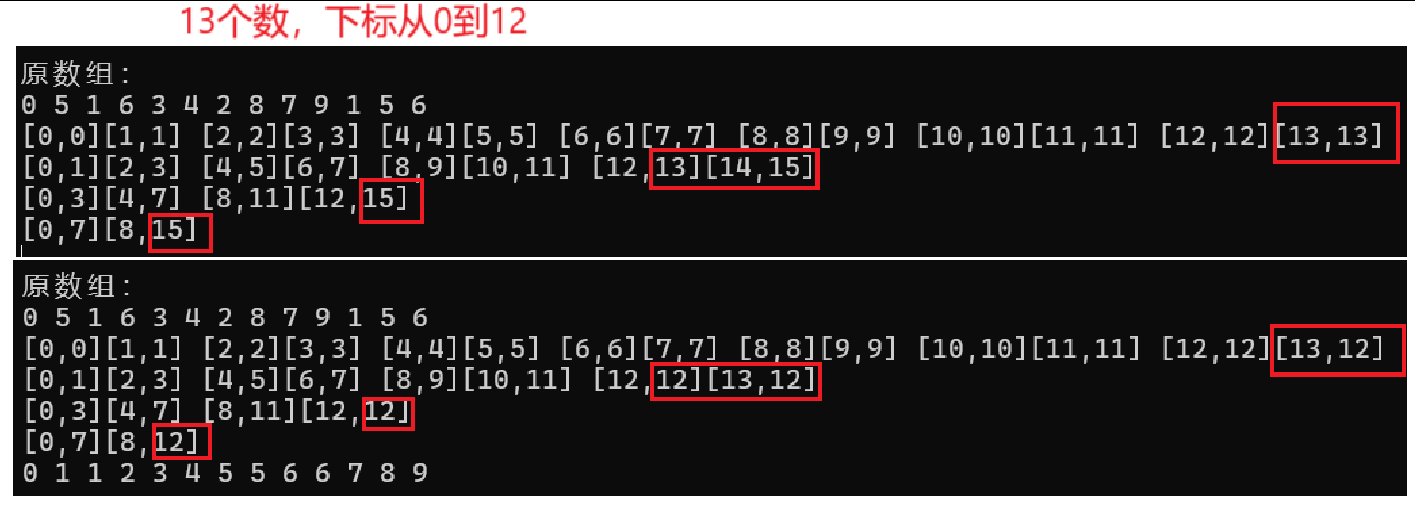
最终区间合理
5.归并排序的时间复杂度与空间复杂度
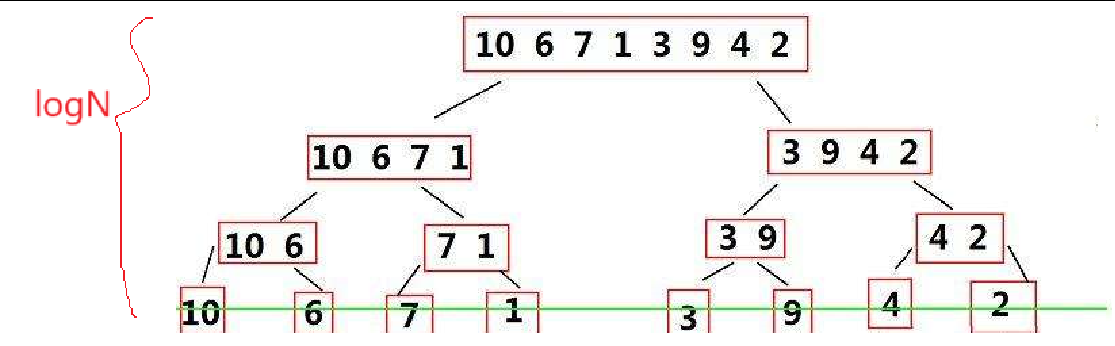
递归实现归并排序需要递归 logN 层,每层进行遍历归并,即每一层遍历N次
所以时间复杂度为O(N*logN)
int gap = 1; while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//........}gap *= 2; }非递归实现归并排序时,外层while循环要循环 logN 次,内层for循环中需要遍历数组中的每个元素,所以时间复杂度为O(N*logN)
递归实现归并排序需要递归 logN 层,所以递归栈的空间复杂度为 O(logN)
又预先在最外层创建了临时数组tmp,临时数组的空间复杂度为 O(N)
由于 O(N) 的增长速度远快于 O(logN),因此 O(N) 是主导项
所以 空间复杂度为 O(logN) + O(N) 约等于 O(N)
非递归实现归并排序创建了一个临时数组tmp,空间复杂度为O(N)








常用类)




主频和时钟配置实验(1))
创建型:生成器模式详解)




