本文参考代码随想录

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

思路

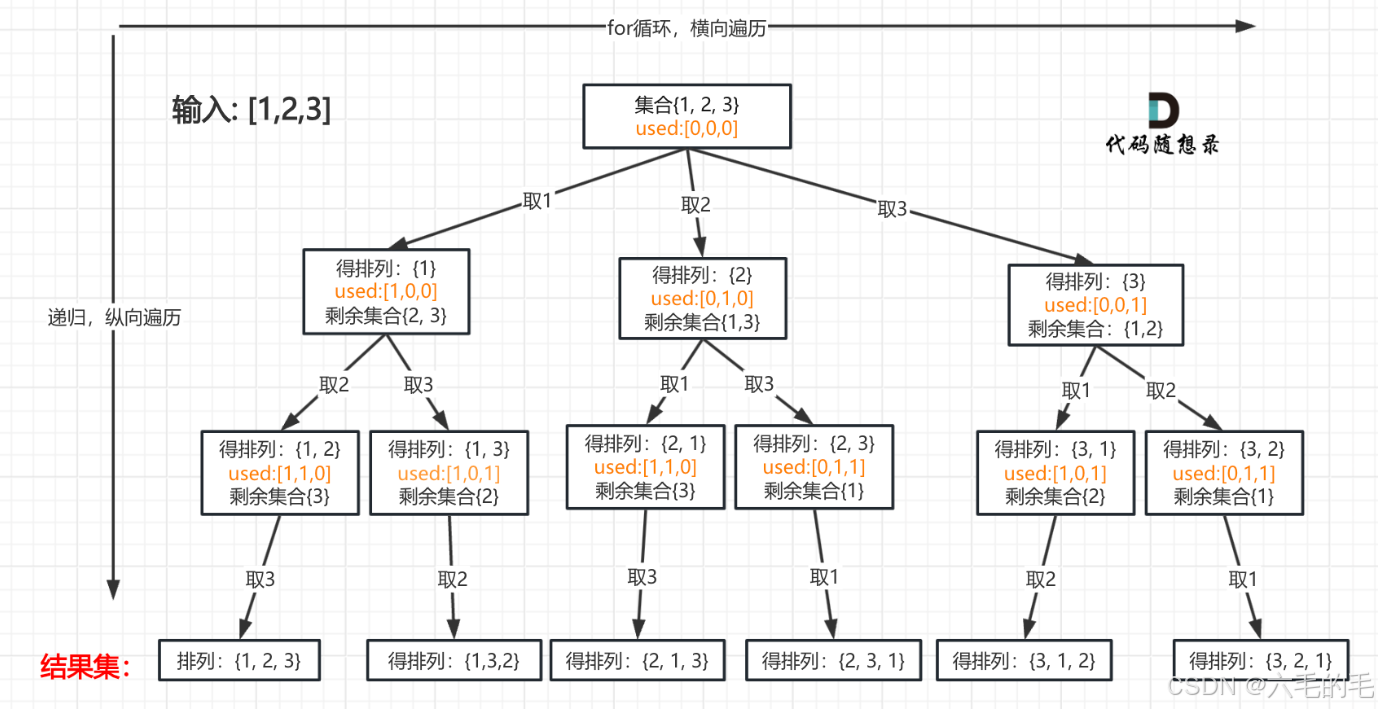
排列是有序的，在排列问题中不需要startIndex；但排列问题需要一个used数组，标记已经选择的元素

当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点，回溯终止。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, vector<bool> used){if(path.size() == nums.size()){result.push_back(path);return;}for(int i = 0;i < nums.size(); i++){if(used[i] == true) continue;path.push_back(nums[i]);used[i] = true;backtracking(nums, used);used[i] = false;path.pop_back();}}
public:vector<vector<int>> permute(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};