接下来需要讲解在连续时间域下的角频率以及在离散化后的数字角频率。

上面可以知道模拟角频率和数字的区别 接下来介绍相位 相位单位是弧度

无频偏：  

对于数字来说是对连续信号采样后的结果，数字的角频率 ，就是相位的递增量，表示每个采样点的弧度变化量

  将n个样本的进行累加就能得出经过n个样本后的相位  θ= *n,  算出相位，此时的相位是无频偏的，是随着采样点数的增加线性增长的，相位也会随之增长，但是转换为频率后会除以样本数，所以输出频率是固定的  θ= 2Πn *f / fs 推出f 频率。

在频偏的情况下：

  相位变成 w2 是基础的角频率和加了频偏的，这时候用  θ= 2Πn *f / fs  得出的F 是频偏后的总频率。

  进行补偿就需要自相关，把基础的角频率w抵消，只剩下角频偏w1 ，也就是经过n个样本，把基础的相位抵消后，只剩下θ = w1 * n带有频偏的相位 ，然后通过F = (θ*FS)/2ΠN  算出频偏。

为啥“自相关把序列自身相位抵消、只剩频偏”？

  补偿：

在知道频偏的情况下，将带有频偏的信号乘一个相反的频率信号，就可以获得补偿后的信号。

FPGA设计中

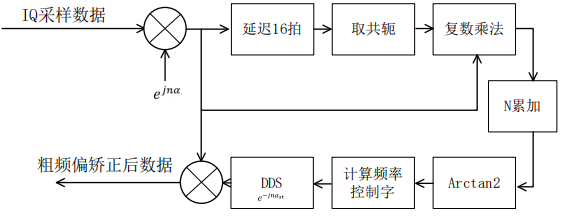
上述是添加了频偏后通过延迟以及共轭i相乘 累加出延迟16的iq信号，然后把累加相位数据转为相位，得到相位就算出频率控制字，用频率控制字控制dds，发出频偏补偿的信号，与原信号相乘得到没有频偏的信号。