原题链接
原题再现
题目描述
给定一个 n 个点 m 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。
输入格式
第一行两个正整数 n,m。
第二行 n 个整数，其中第 i 个数 ai 表示点 i 的点权。
第三至 m+2 行，每行两个整数 u,v，表示一条 u→v 的有向边。
输出格式
共一行，最大的点权之和。
题意简述
有向图，点都有点权。点可以经过多次，但点权只能加一次。
求这张图的最大权值。
解题思路
如果一个强连通分量上的某个点被选中，那么选择整个强连通分量显然更优。因为这样可以最大化点权总和。这样一来，可以把整个强连通分量视为权值为强连通分量中所有点权值之和的整体点，选择这个强连通分量上任意一点就意味着选择整个强连通分量。所以缩点。
缩点，也就是将强连通分量合并为单点，将原来k个强连通分量的图简化成只有k个点的有向无环图（DAG）。Tarjan算法实现。
Tarjan算法
在DFS搜索遍历整个图的过程中，把有向图划分为DFS搜索树及非树边。
与传统的DFS不同的是，多了回溯这一步。
非树边可以被分为：
- 返祖边（回边）：从树上的后代指向祖先，如7→1。
- 横叉边：无直接祖先关系且分属不同子树，如9→7。
- 前向边：从树上的祖先指向后代，如3→6。
在遇到非树边时，有相应的操作。
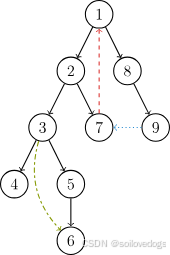
如果结点 u 是某个强连通分量在DFS搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在DFS搜索树中以 u 为根的子树中。结点 u 被称为这个强连通分量的根。
关键数据结构
- 数组dfn：dfn[i]表示第一次发现i的时间戳，亦可判断是否为被访问。
- 数组low：low[i]表示i的追溯值，u或u的子树能够追溯到的最早的栈中节点的次序号。
- 数组vis：vis[i]表示i是否正在访问，即是否在栈中。
- t：时间戳。
- scc：强连通分量个数。
- 栈st：栈保存了当前深度优先搜索（DFS）路径上的所有节点。这些节点可能属于同一个强连通分量，但尚未确认是否构成完整的SCC。用于追溯。
- 数组color：每个节点标记其所属的强连通分量编号。
void tarjan(int v) {dfn[v] = low[v] = ++tot; //标记dfn[]访问顺序，还有low[]的初始值sta.push(v); //让点v进栈vis[v] = true; //标记这个点被访问过for (int i = head[v]; ~i; i = edge[i].next) { //一直循环这个点每一个出度，直到-1表示没有了，这也是为什么memset head数组时要赋-1int u = edge[i].to; //定义u并把它赋成这条边的终点if (!dfn[u]) { //如果u没有被访问过tarjan(u); //找下面这个点low[v] = min(low[v], low[u]); //这个点low[v]的值就是当前low[]的值与找到的u点的low[]值} else if (vis[u]) //如果u被访问过了，但是还在队列中low[v] = min(low[v], dfn[u]); //low[v]就取这个点的low值与循环到的点u的dfn[u]的最小值}if (dfn[v] == low[v]) { //如果发现v这个点的dfn[]和low[]相等，说明这个点是一个强连通分量的“根”。sccnt++;int u; //定义u变量，作为栈顶元素do { u = sta.top(); //将u赋值为sta栈的栈顶元素vis[u] = false; //将u弹出sta.pop(); //同上color[u] = sccnt; //将u标记为这个强连通分量里的点} while (v != u); //当v == u之后，结束循环}
}
参考文献
强连通分量 - OI Wiki
速通Tarjan与强连通分量
全网最最详细！一文讲懂Tarjan算法求强连通分量&缩点 - 淼畔 - 博客园
tarjan算法详解--关于图的连通性 & 连通分量 - 知乎
tarjan算法总结 (强连通分量+缩点+割点)，看这一篇就够了~_强连通分量切割-CSDN博客
浅谈 tarjan-腾讯云开发者社区-腾讯云
Tarjan-1972.pdf
深入浅出 Tarjan 算法 (一)
60 分钟搞定图论中的 Tarjan 算法（一） - 知乎
写在最后
说实话，我作为初学者，学这个算法的时候挺吃力，看了不少网上的算法书（原因就是把算法书全都忘在学校了QAQ），可能是鄙人智力有限的原因吧。所以我决定自己录一个视频，演示一下这个过程。
)
