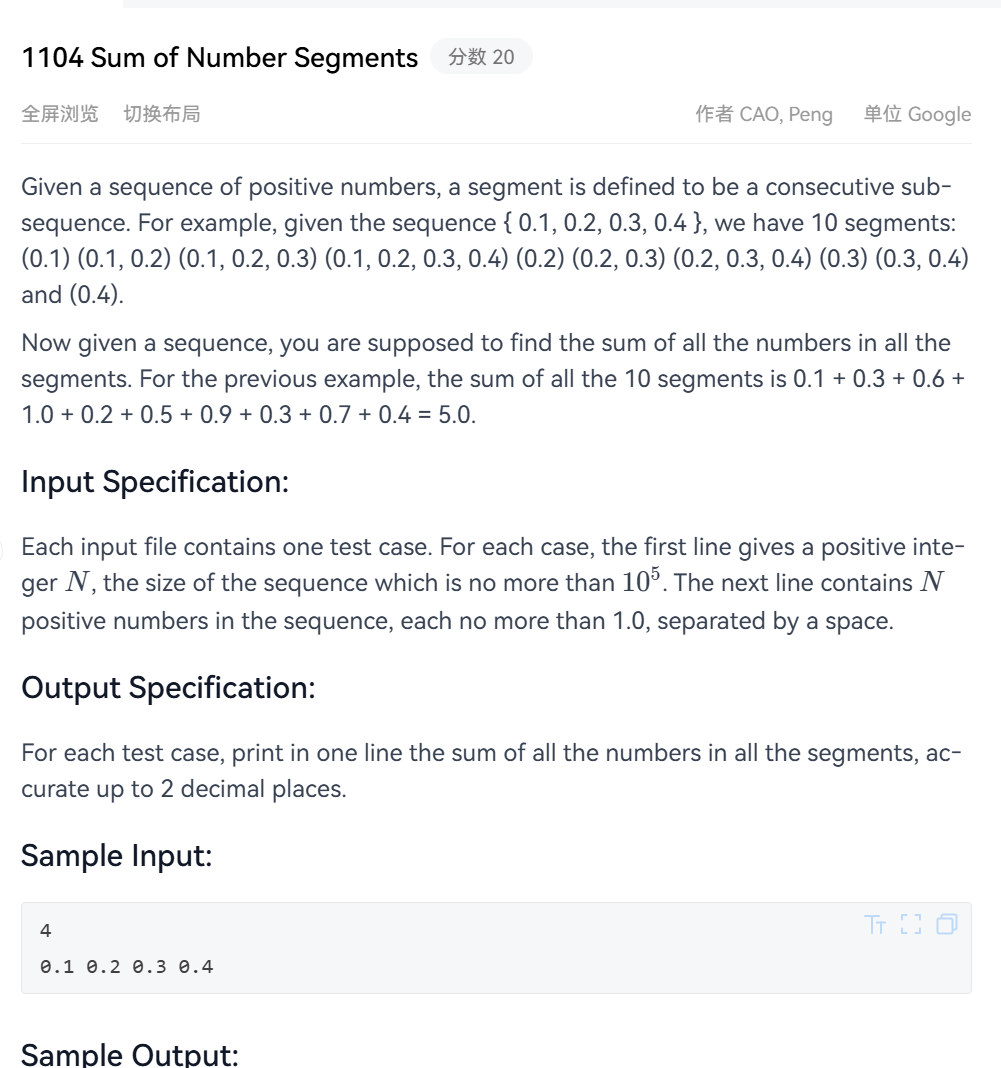
这一题的大意就是找一个数组中的所有子数组，它们的累加和为多少，
题目上给出的数据范围是O(n^5)那么只能遍历一次，不能用暴力的方法求出。
看到这一题我有两个思路：
1.试图用双指针和滑动窗口来把O（n^2)的时间复杂度降到O（n）
但我忘了双指针的特点：
双指针常见场景是「满足条件的最长/最短子数组」，比如「和 ≤ K 的最长子数组」。
但是这题要的是 所有子数组的和，没有任何“限制条件”。
所以双指针无法避免枚举所有子数组 —— 它本质还是会走到 O（n^2)
2.另一种思路是用动态规划，找到每一个以i为底的子数组的和，把它们累加就可以了。
正确的思路确实是这样的
但我在递推的时候却弄错了，没有看出来dp[i]=dp[i-1]+a[i]*i;以i为底的子数组的和就是以i-1为底的子数组的和，再把每一个子数组的后面加上一个a[i]，总共就是加上a[i]*i.
当时没有想出来。实际上也就是找规律吧
正确代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <unordered_map>
#include <limits.h>
#include <queue>
#include <string.h>
#include <stack>
using namespace std;
int N; 
long double a[100005];
long double dp[100005];
long double ans;
int main()
{cin>>N;for(int i=1;i<=N;i++){cin>>a[i];}for(int i=1;i<=N;i++){dp[i]=dp[i-1]+a[i]*(long long)i;ans+=dp[i];}printf("%.2Lf",ans);return 0;} 

要注意当i很大的时候，可能会溢出，毕竟最大只能为10^9,举一种极端的情况的例子，假设a[i]都是1，那么
dp[1]=1
dp[2]=1+2
dp[i]=1+2+…+i
dp[n]=1+2+++…10^5;
等差数列求和dp[n]：
10^5 * (1+10^5)/2= (10 ^5 + 10^10)/2
而dp[n-1]= (10^5-1)(10 ^ 5)/2
dp[n-1]+dp[n]约等于10^10 就已经超出了范围 10^9了
更不用提前n-1个dp表了
ans的值一定是溢出的，因此需要开long double
注意输出是%Lf 是大写的L。
我看其他人的题解都是把这道题看作是一个数学找规律的题目
每个元素 a[i] 在多少个子数组中出现？
对于每一个元素a[i]它前面的数可以有多少种情况呢？
1…i一共是i种，而它后面的数有N-i+1种，为啥+1，因为可以a[i]开始a[i]结束。
所以a[i]出现的值的和就是 a[i]*(N-i+1)*i
只需要把每一个元素累加起来即可了。
这种思路感觉不如我以a[i]为结尾的子数组的和的思路好想。（可能是先入为主的原因。）
总结：
这一题因为数据范围的原因会溢出：
不认真带入数据试的话，还不好看出来是溢出的。
另一方面就是找规律，动态规划了
建议找几个例子试一试可以发现规律。