• 积分变换常应用于解微分方程

---

微分方程的解法：

• 时域经典法；
• 频域变换法；

---

“积分变换”最初并不是为了解微分方程，而是出于更“纯粹”的数学动机——理解函数的结构、求解代数或几何问题，以及简化复杂的积分运算。微分方程的求解，是后来人们意外发现的一个“副作用”，却最终成了积分变换最重要的应用之一。

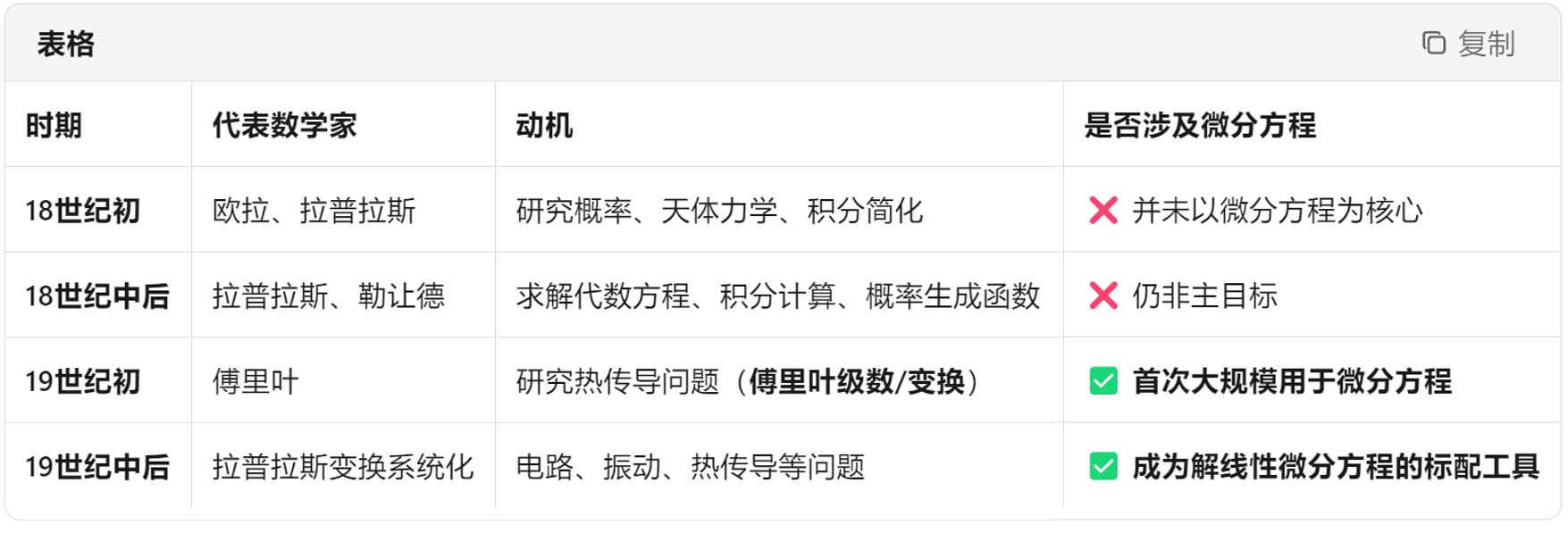
18世纪的时候数学界的一个大热门方向就是用积分变换来求解微分方程，那时候大家都纷纷推出自己的积分变换。欧拉、拉格朗日、傅里叶、拉普拉斯……

拉普拉斯在1785年推出自己的积分变换公式，但他只是把这个积分变换当作一个求解微分方程的中介转换，并且他自己也并不清楚这个变化到底表示了什么。

直到在研究了傅里叶变换之后，拉普拉斯才明白了，变换里的S原来是表示复频率。

由复频率构成的区域称为复频域，也被称为拉普拉斯域，简称拉氏域。

拉普拉斯变换也就是从时域到复频域的变换。

复频域可以理解为一个复平面，平面上的每一个点都代表了一个复频率。

而每个点之上都有一个变化的幅值，所以一个复频域上的频谱图，就成了一个三维立体图。

而它沿着虚轴的切面，就是傅里叶变换的二维频谱图。

傅里叶变换是拉普拉斯变换的一个切片，但是拉普拉斯变化仅在适用范围更广，算不上傅里叶变换的升级版，因为这两个变换聚焦的应用领域不同。

这两者是在交叉发展的同时，在应用中不断进化，才在多年后有了形式上的相似与统一。

0. 积分

积分就是函数求和。

实数求积运算：点乘。

函数求积运算：卷积。

求积是求和的拓展，卷积也是以积分的形式进行运算。

1. 傅里叶变换

1.1 角频率

频率

• 概念：每秒钟完成动作的次数。
• 单位：赫兹，Hz。

角频率

• 概念：每秒钟“转圈动作，角度变化”的频率。
• 单位：弧度/秒，rad/s

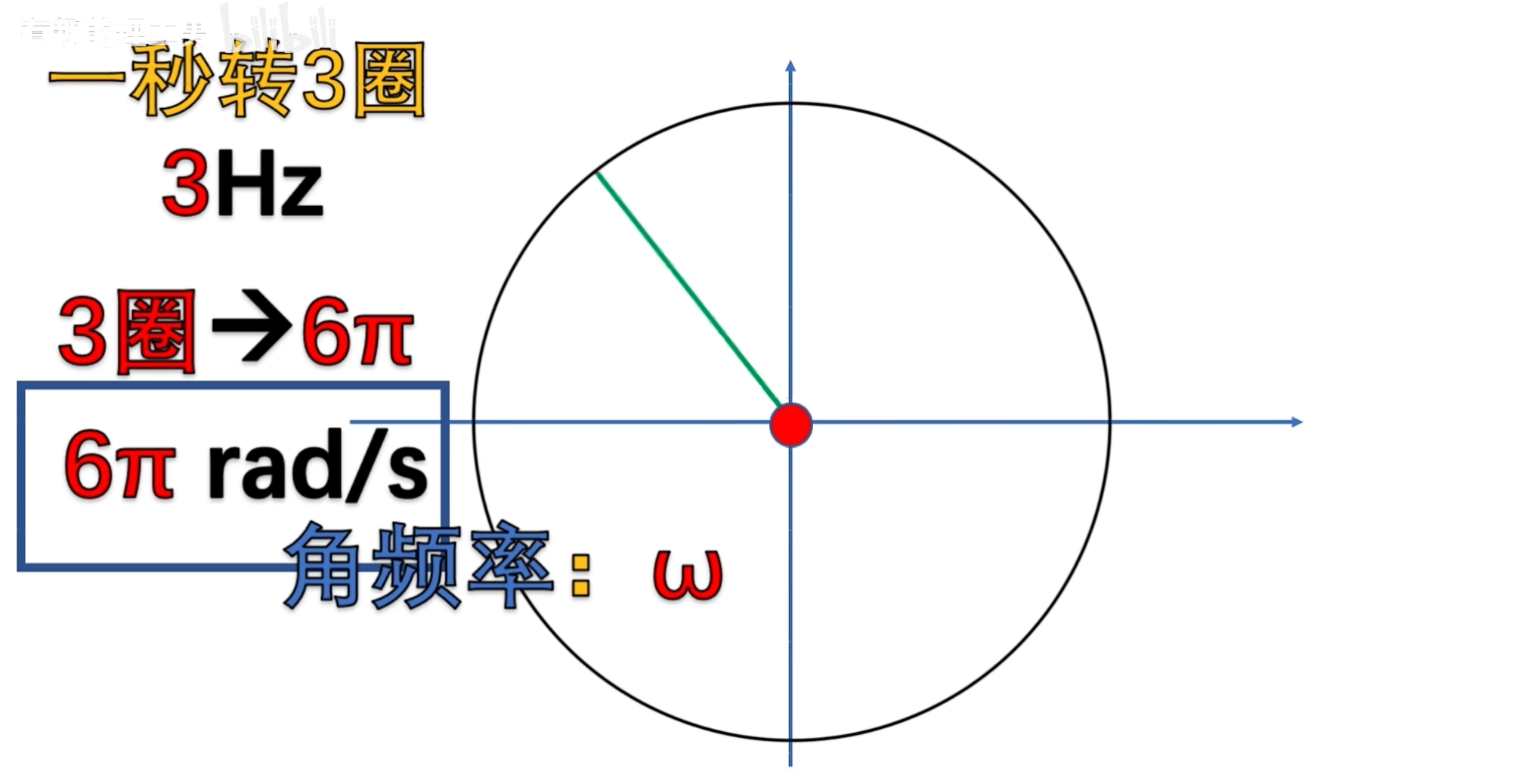
角频率与正弦函数

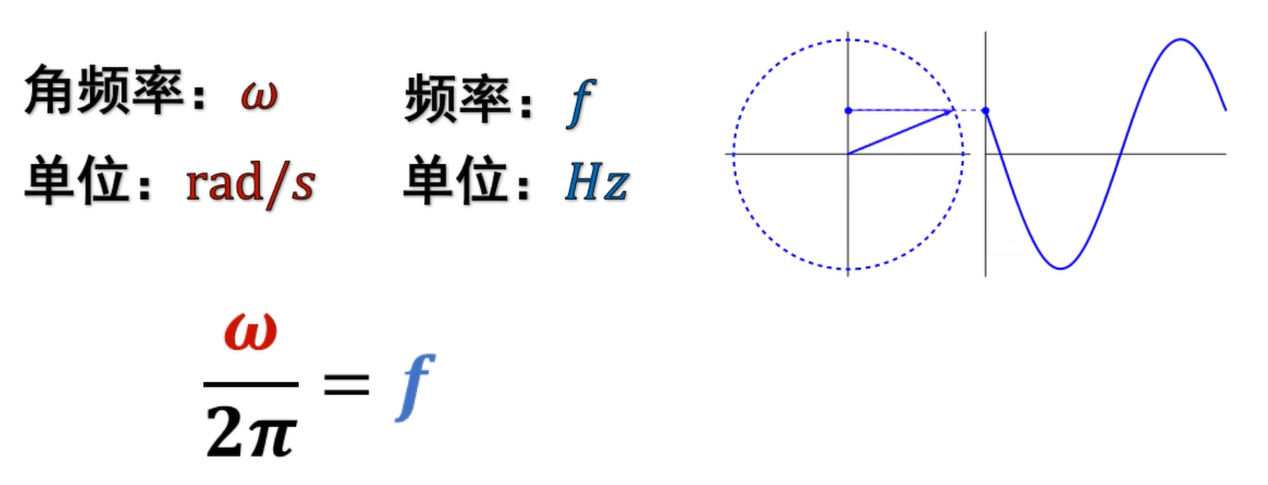
正弦函数在直角三角形中的定义是：直角边与斜边的比值。

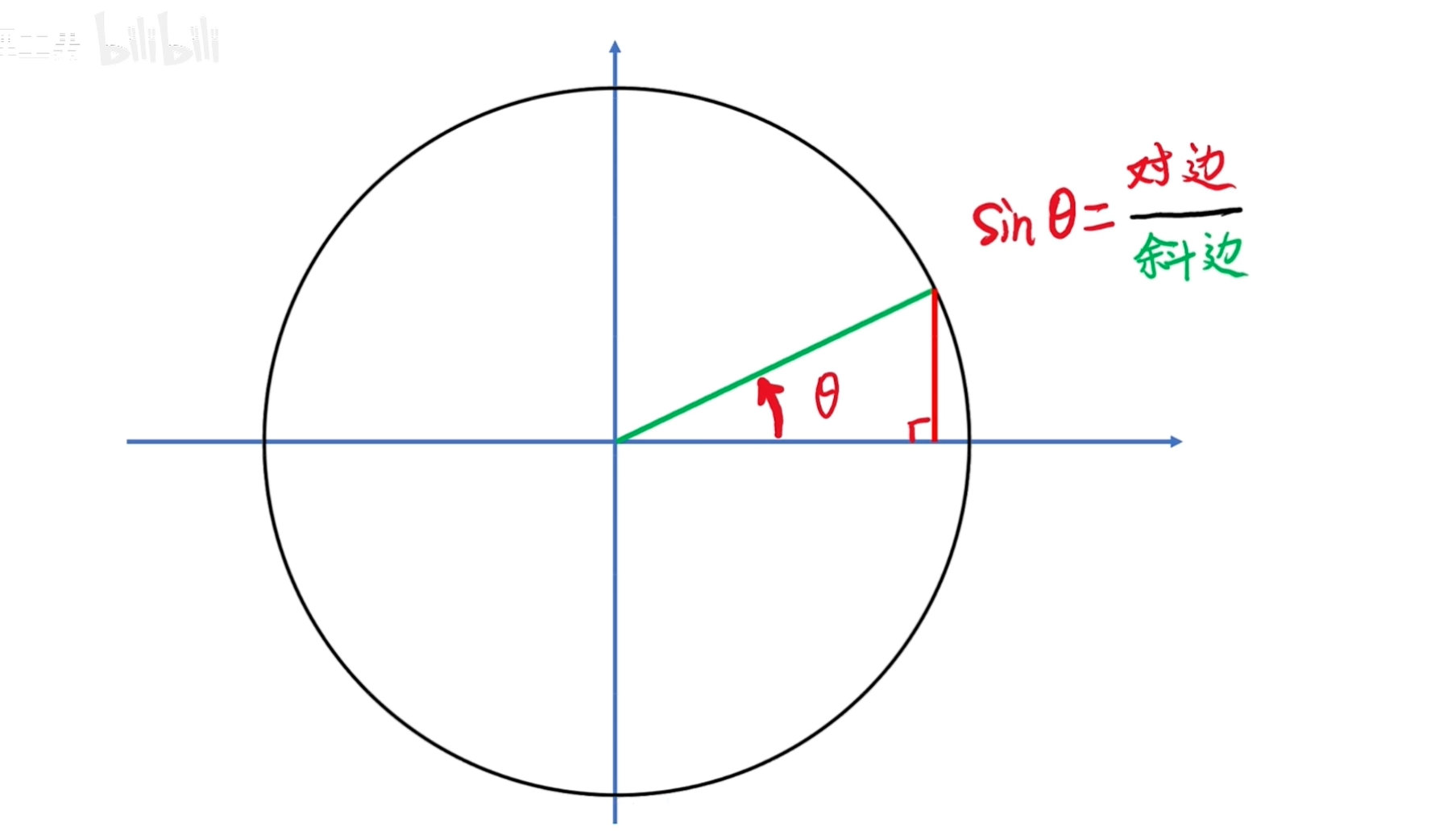
这个夹角的正弦值就是红边与绿边的比值。

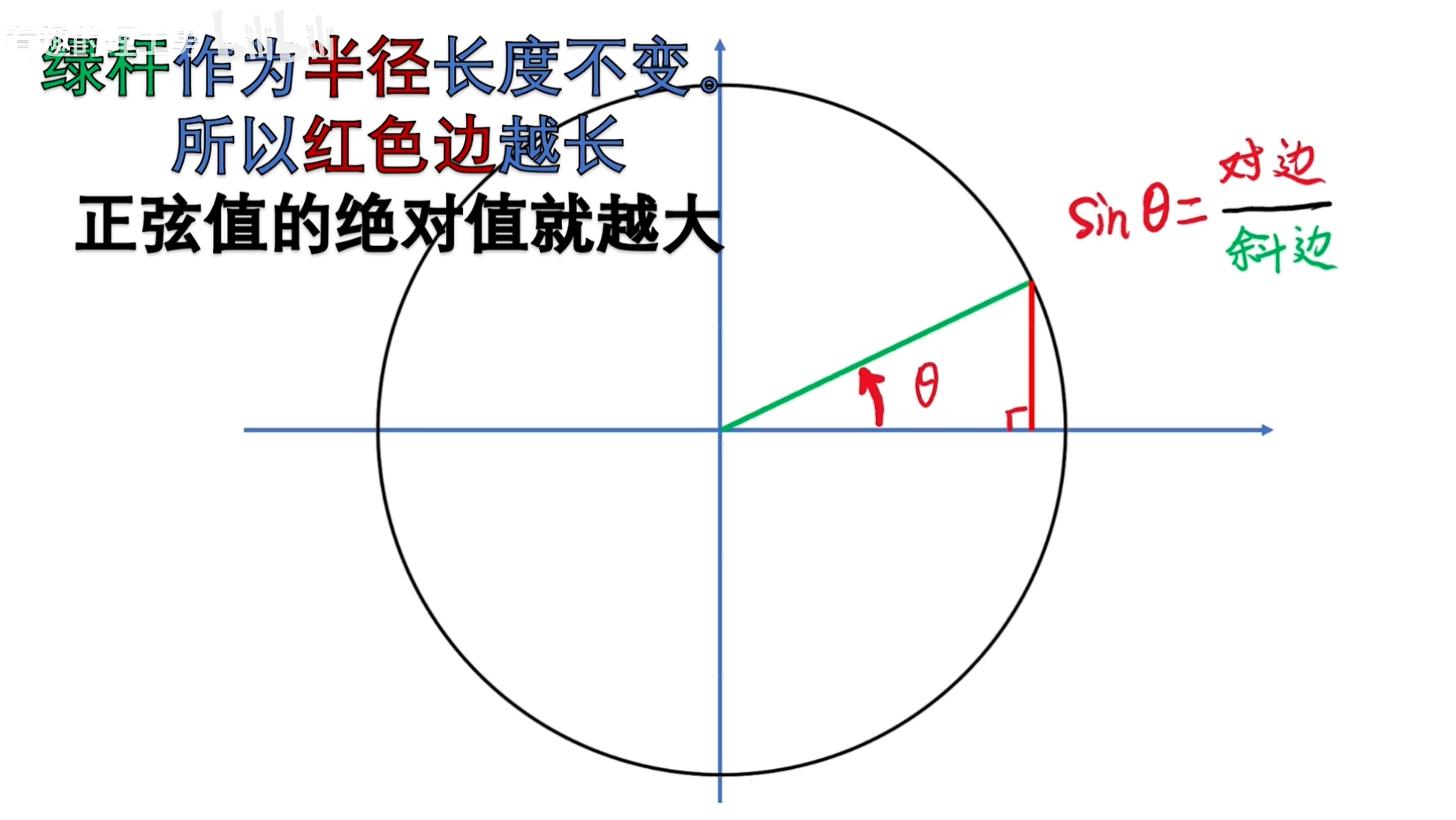
变化的角度可以用角频率乘以时间来表示：θ = ωt。

所以正弦值可以转换表示为：sinθ = sin(ωt)。

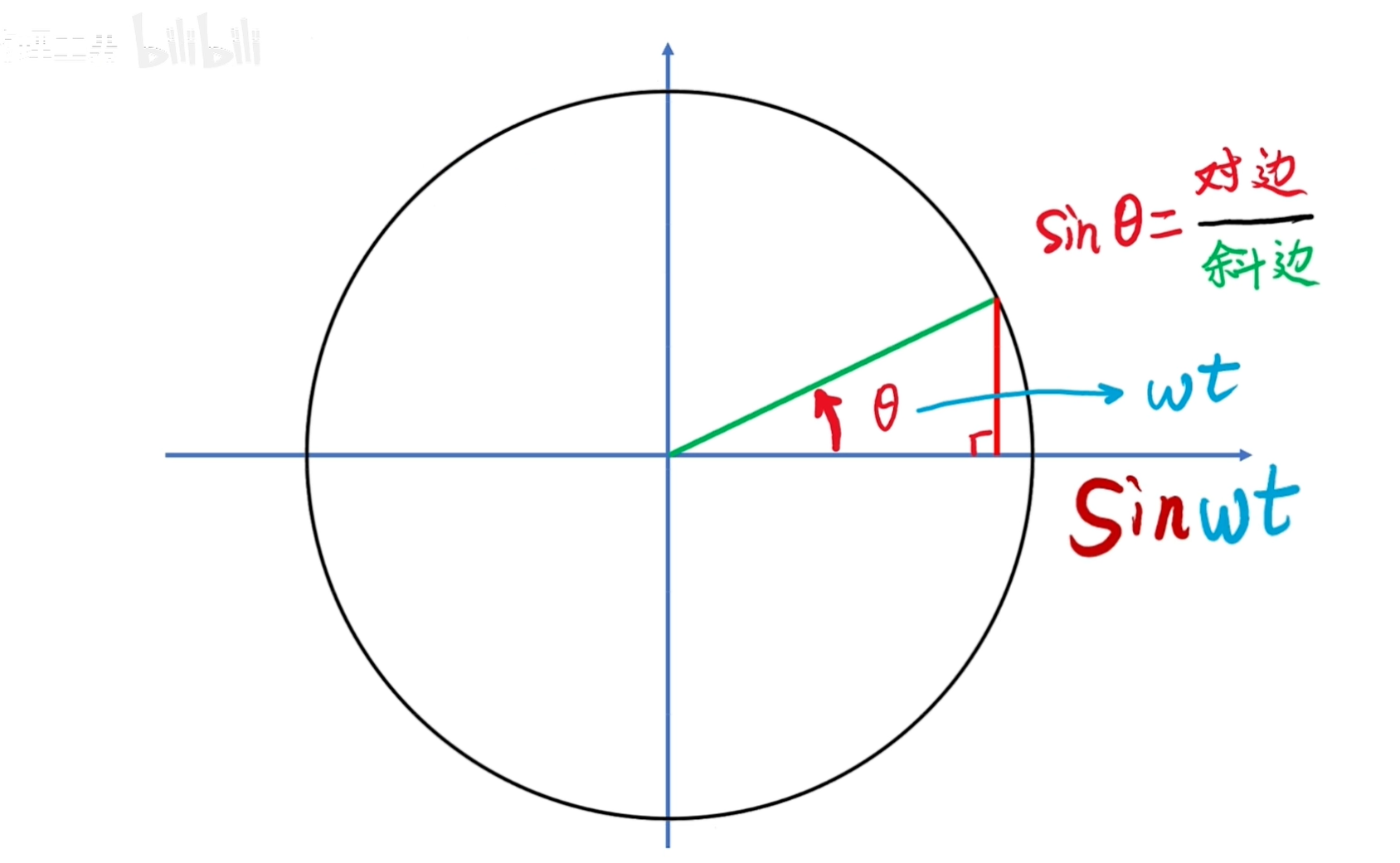
表示正弦值是时间的函数。

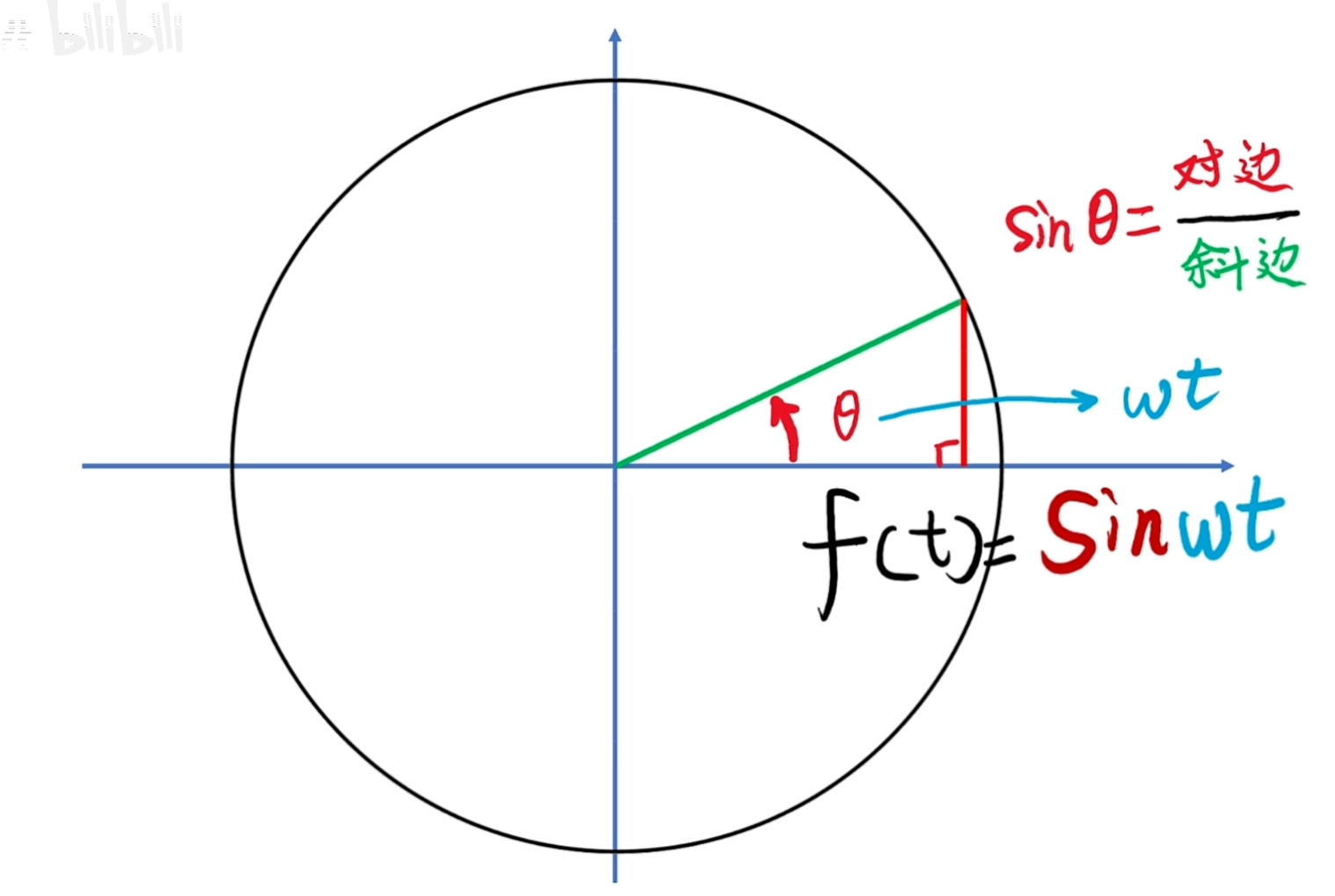
把转圈的动作加上一条时间轴，让旋转的动作沿时间的方向前进，它就形成了一个立体的螺旋形状。

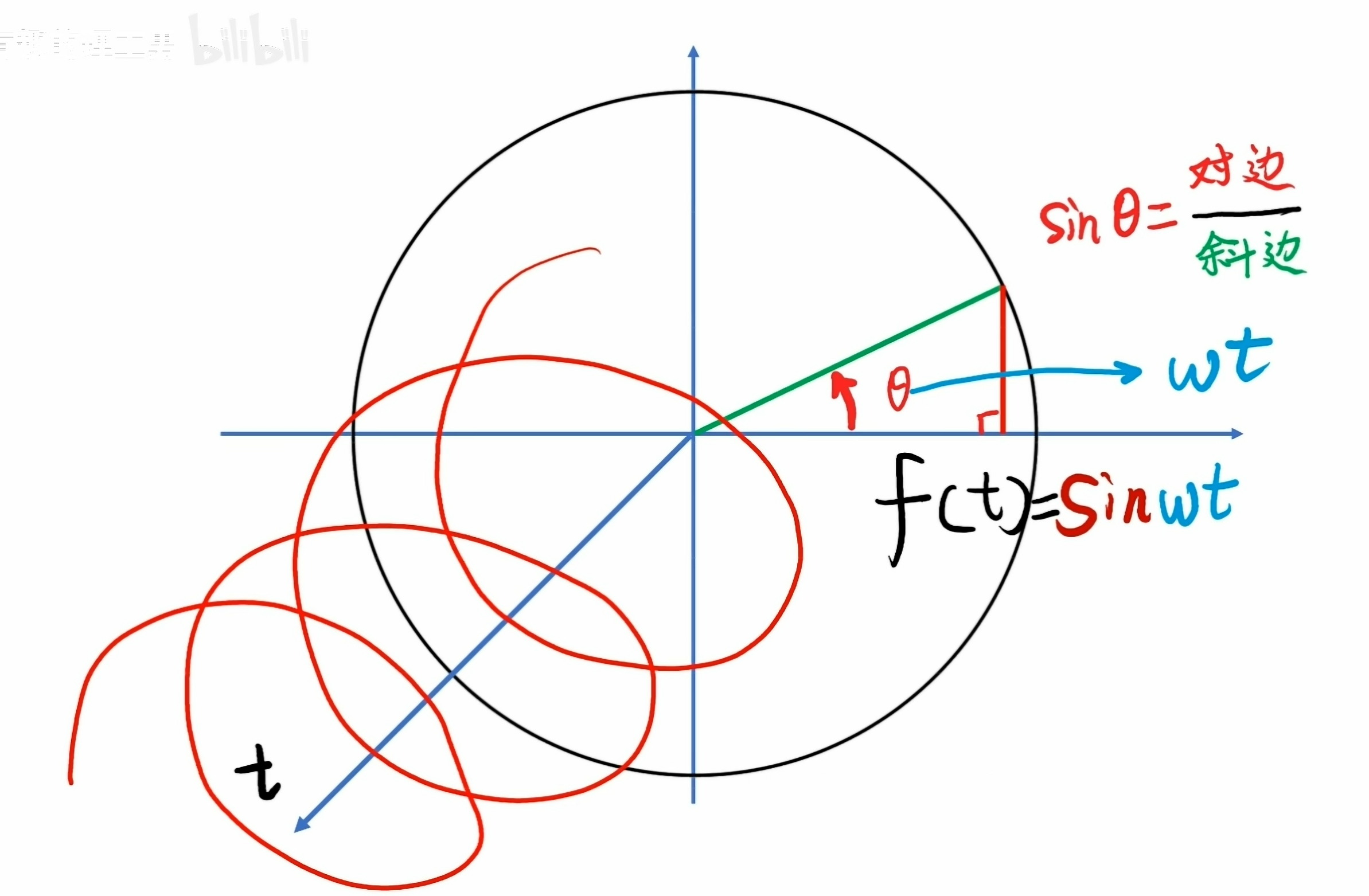
就像拉开的弹簧一样。从正面看过去它还是一个圆圈，它在那里转。

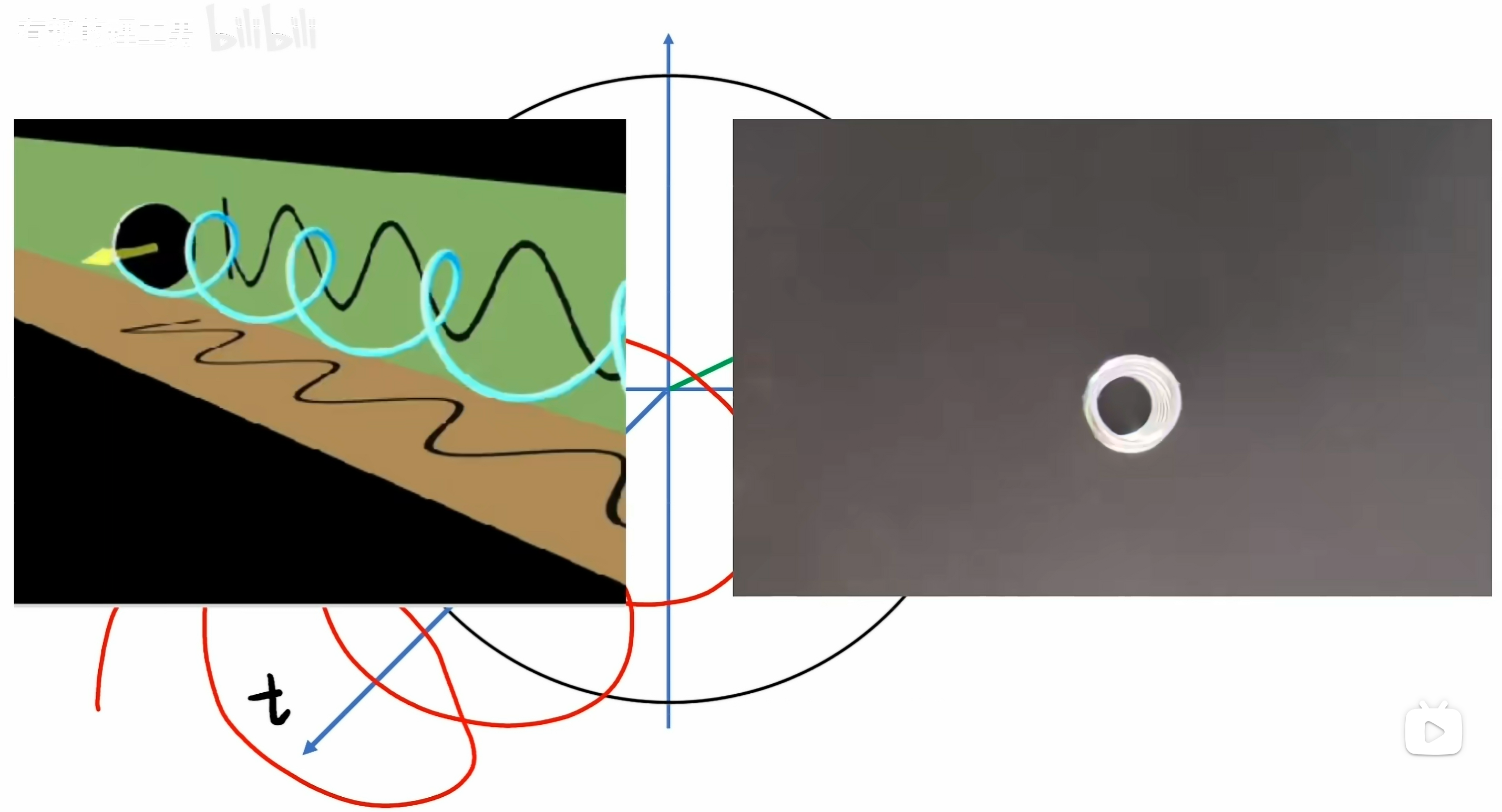
从侧面看，即把时间轴展开了，就看到了一个正弦波形。

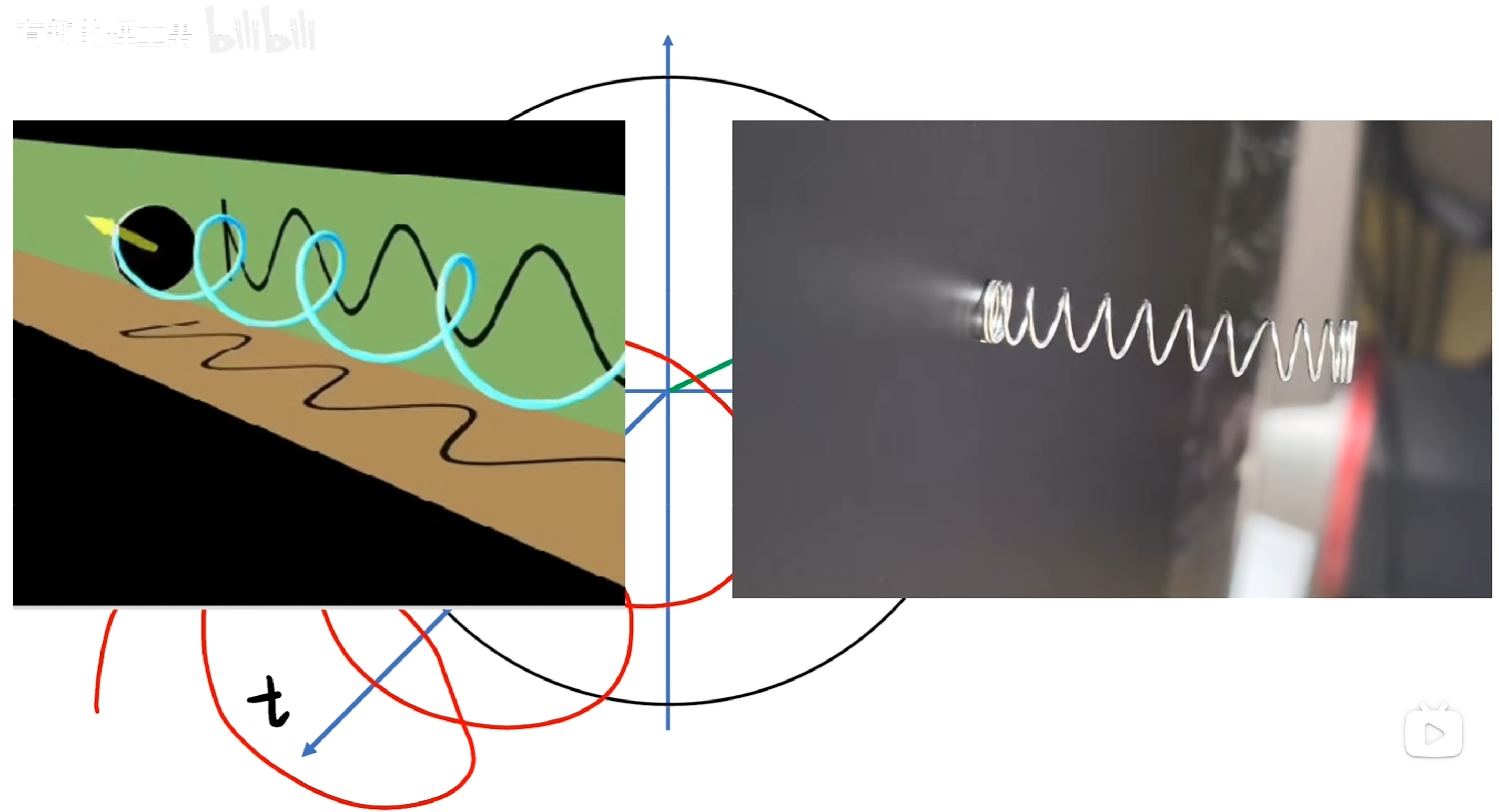
当这个角频率越大，也就是旋转得越快的时候，从侧面看的正弦波形就更紧凑。

傅里叶级数就是把一个复杂信号分解成很多个正弦信号的叠加：

区分这些正弦波形的最明显的特征就是——角频率：ω。

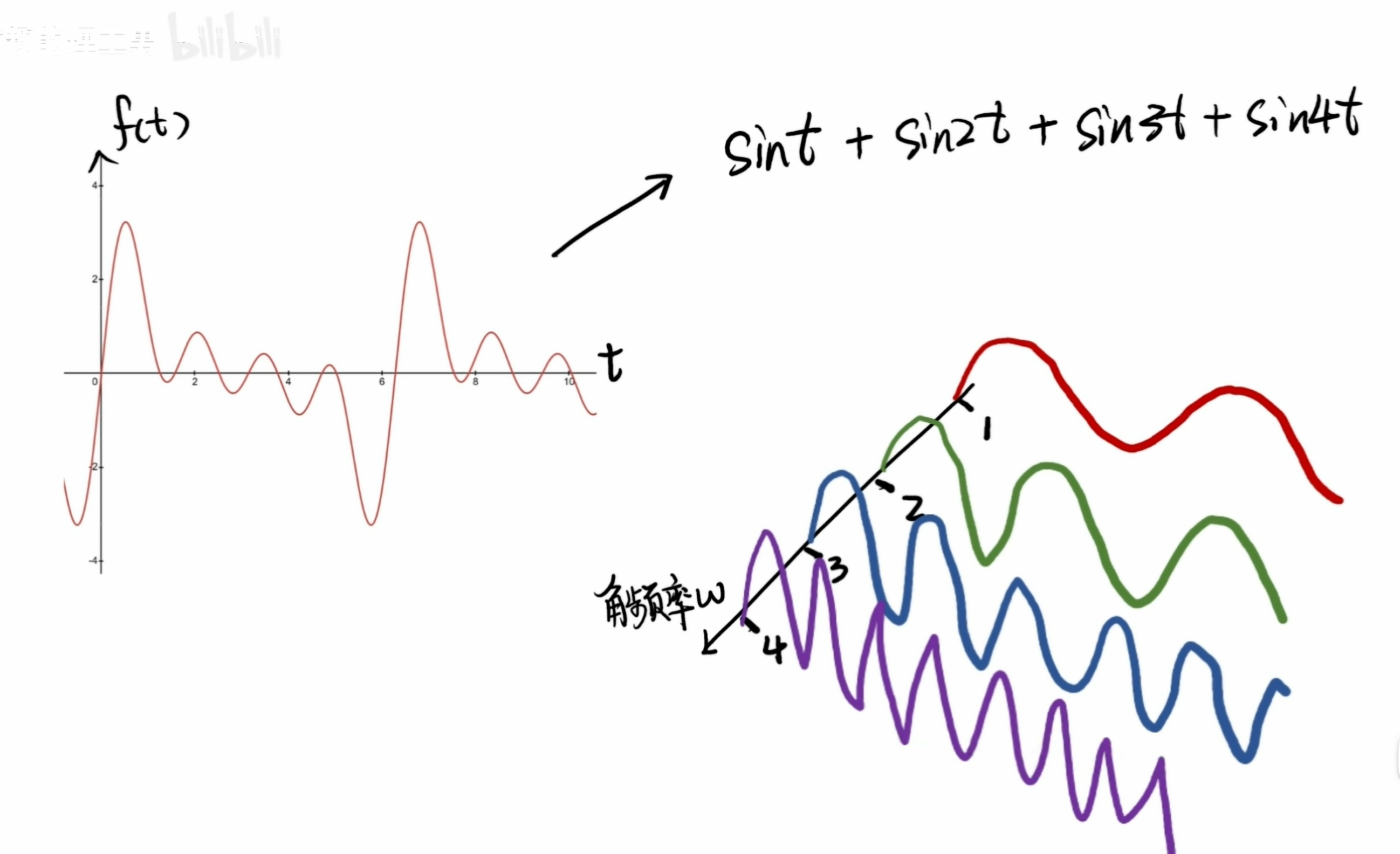
已知复杂信号f(t)可以拆分成上述的三角函数组合，那么就可以建立一条角频率的轴，然后再按这个顺序把这些正弦波形给放置好。——这其实就是傅里叶变换里的频域，即取频率为自变量对信号进行分析。

1.2 傅里叶变换简介

以信号分析为例，下面是红绿黄交通信号灯：

不同颜色的信号的频率是不一样的。

若是交通灯的规律是：红8秒、黄3秒、绿10秒。

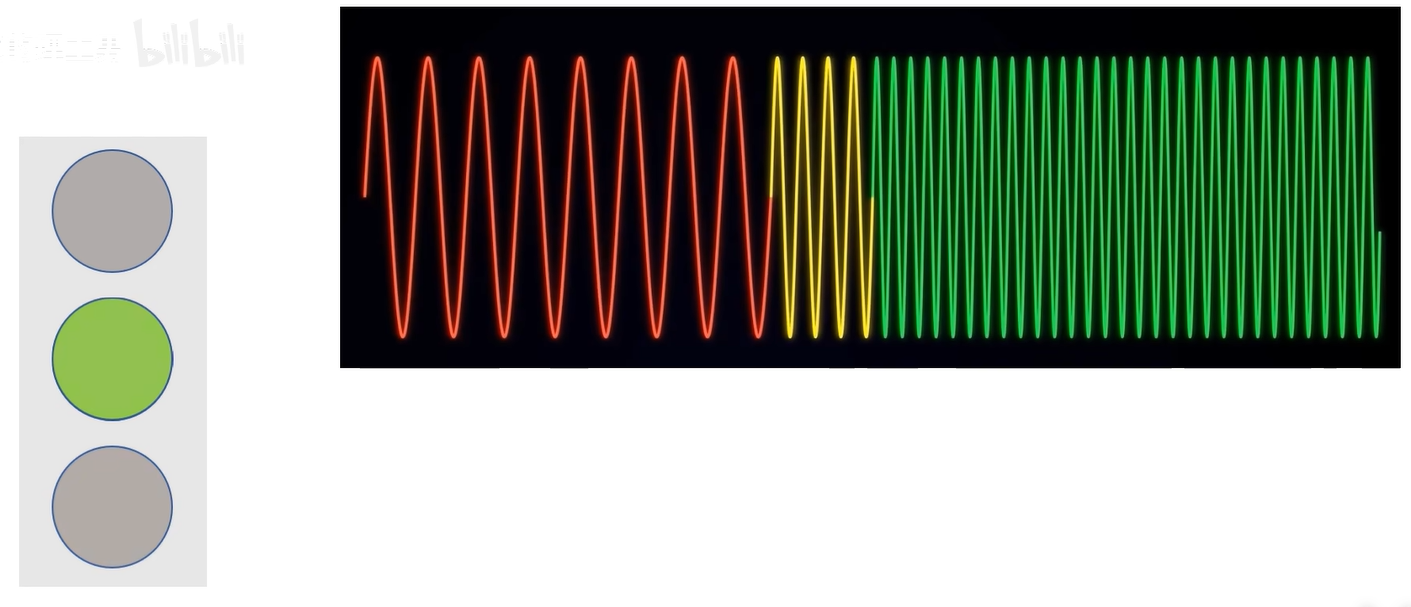
那就可以在坐标轴上绘制出来，得到一个随时间变化而变化的信号函数。这就是信号的时域表达。

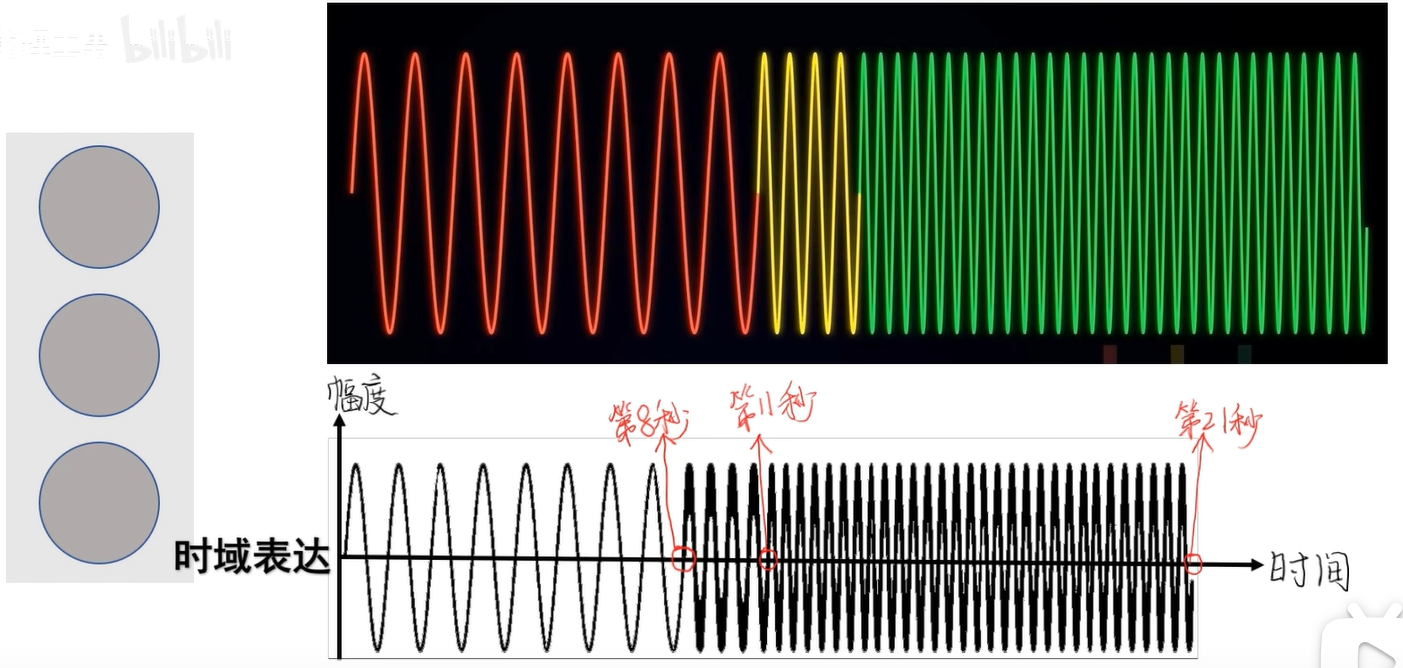
灯坏了，三个灯同时亮，这些信号在时间上有重叠，波形就会叠加，用时域的表达就会很看起来很混乱，也看不出有哪些频率成分。

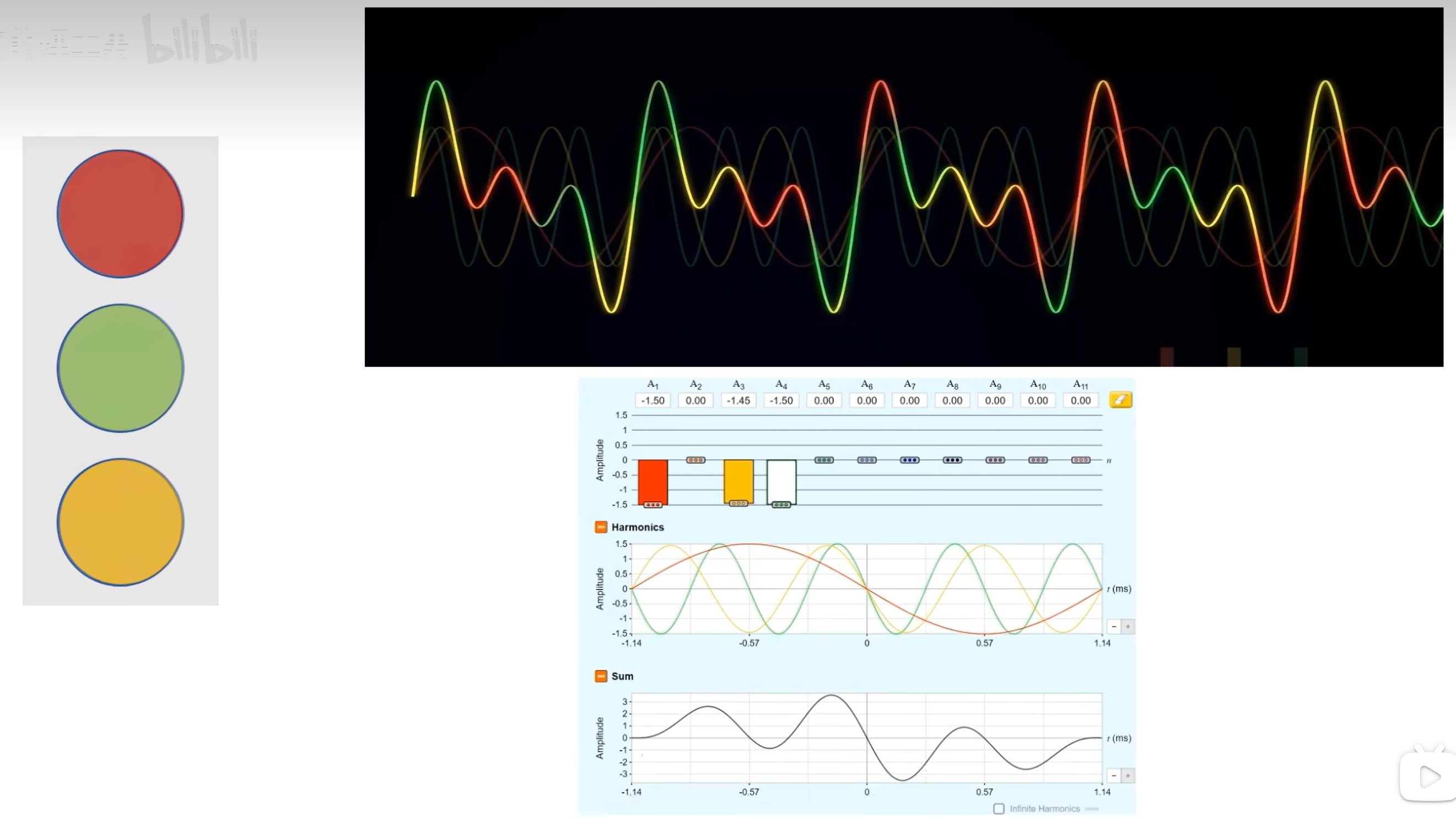
傅里叶变换可以让我们把这些混叠在一起的信号分拆开，让我们知道这个信号是由哪些频率成分构成的。

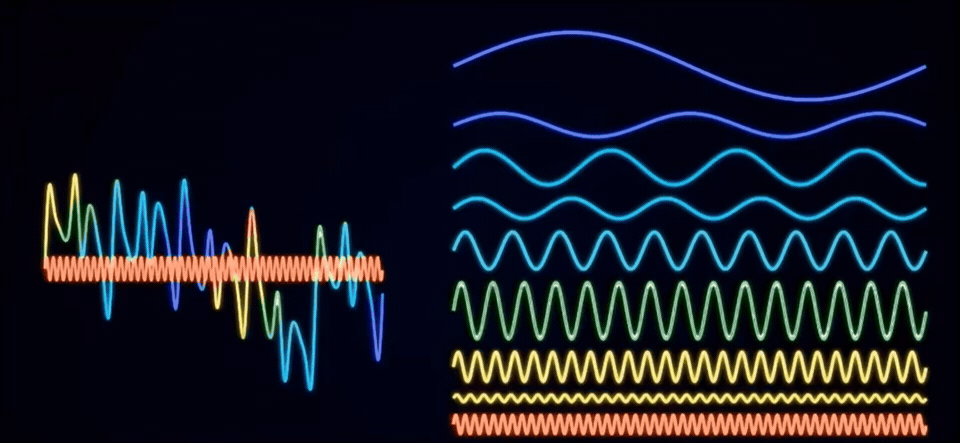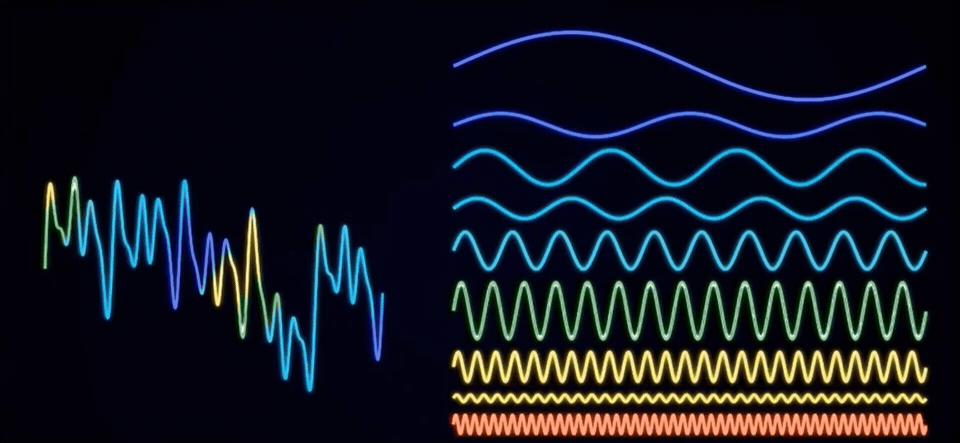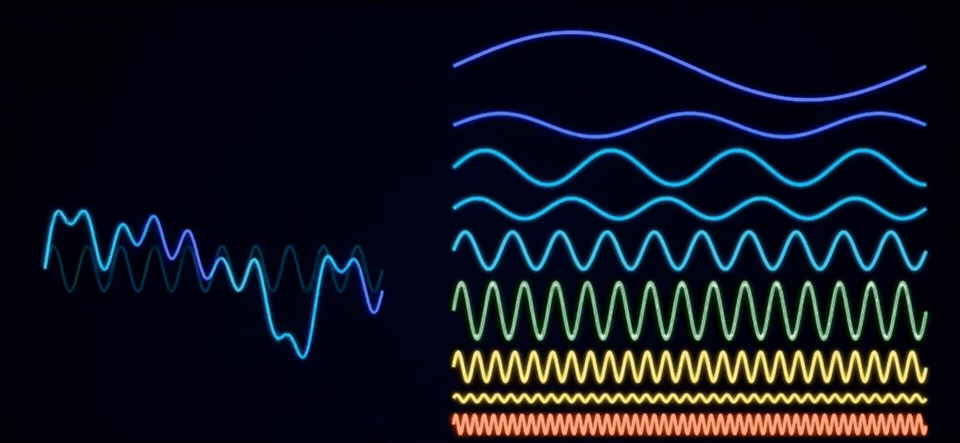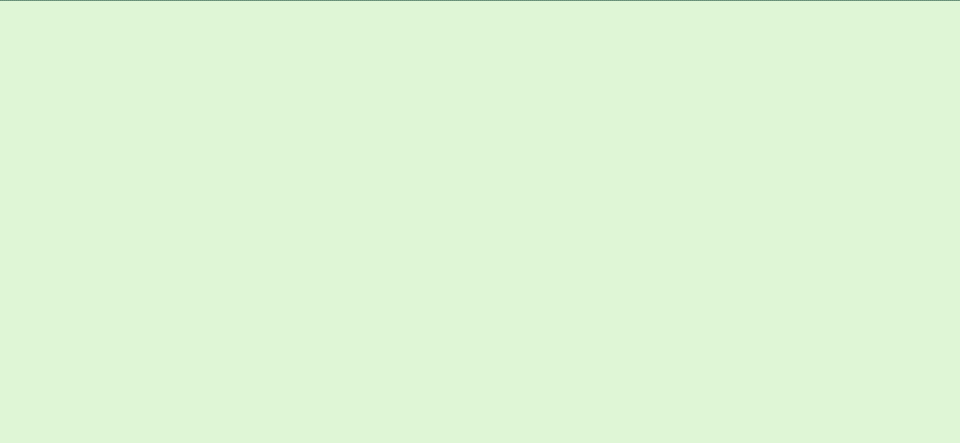
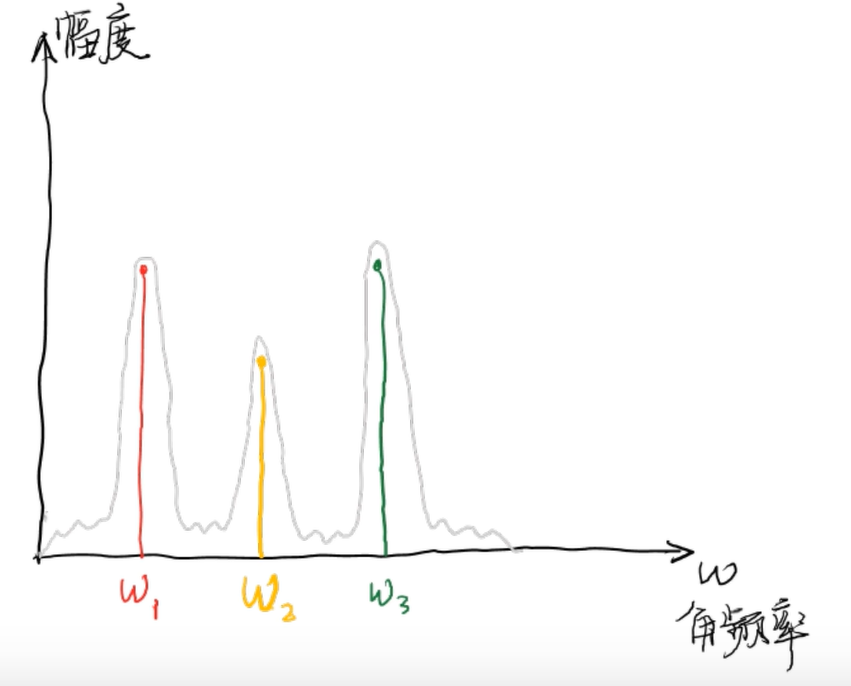
例如刚才的信号经过傅里叶变换之后就成了这样，从侧面看拆分后的频率投影，其实就是频域图。

（幅频图）

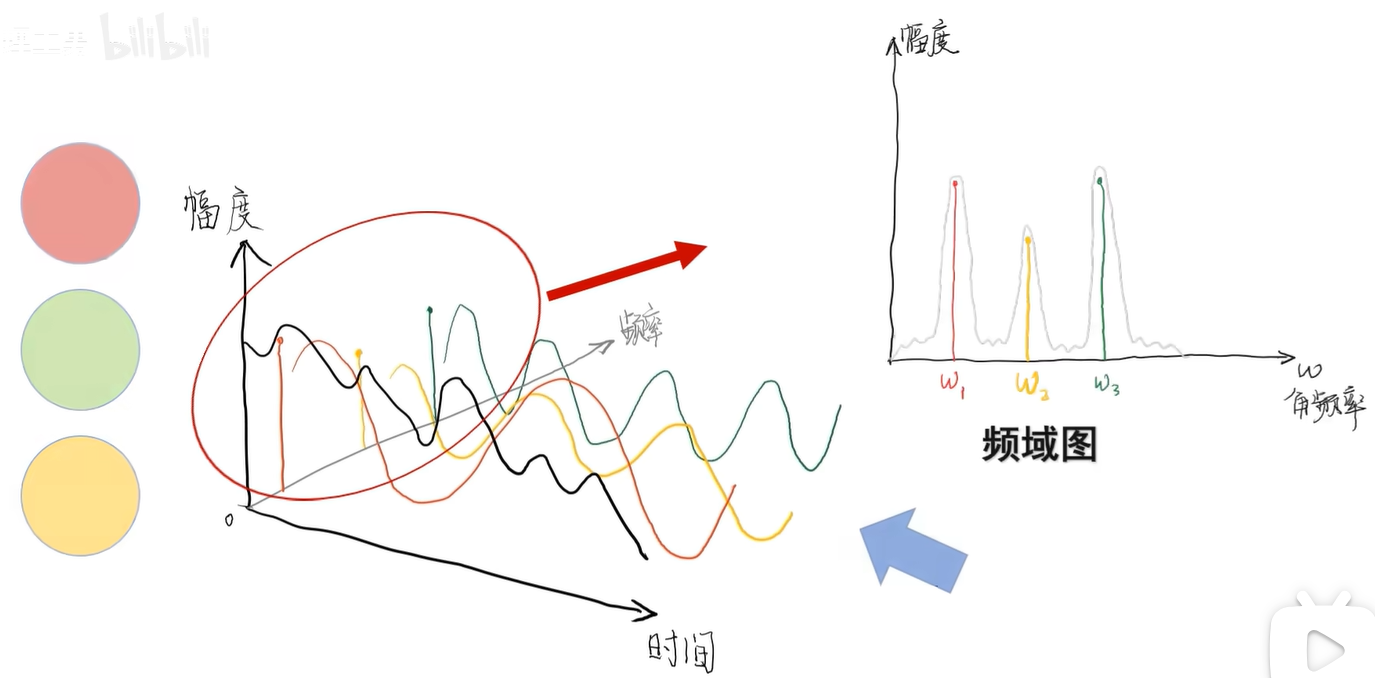
引入频率信息的代价是牺牲掉时间信息，可以用小波变换取时域、频域的平衡。

频域图的横坐标是角频率：

这个图的ω1、ω2、ω3位置有3条竖线，分别代表红、黄、绿三个信号，高度代表强度，即振幅。

这是关于角频率的函数，故而也把变换后的信号称作频域的信号。

傅里叶变换能够帮助我们完成从时域到频域的转换，但是傅里叶变换也有局限性。

1.3 傅里叶变换的不确定性原理

频域图看不出时间的变化，因为从侧面看它就是一条线。

以信号灯为例，无论信号灯以何种组合形式来闪动，频域图是不变的。

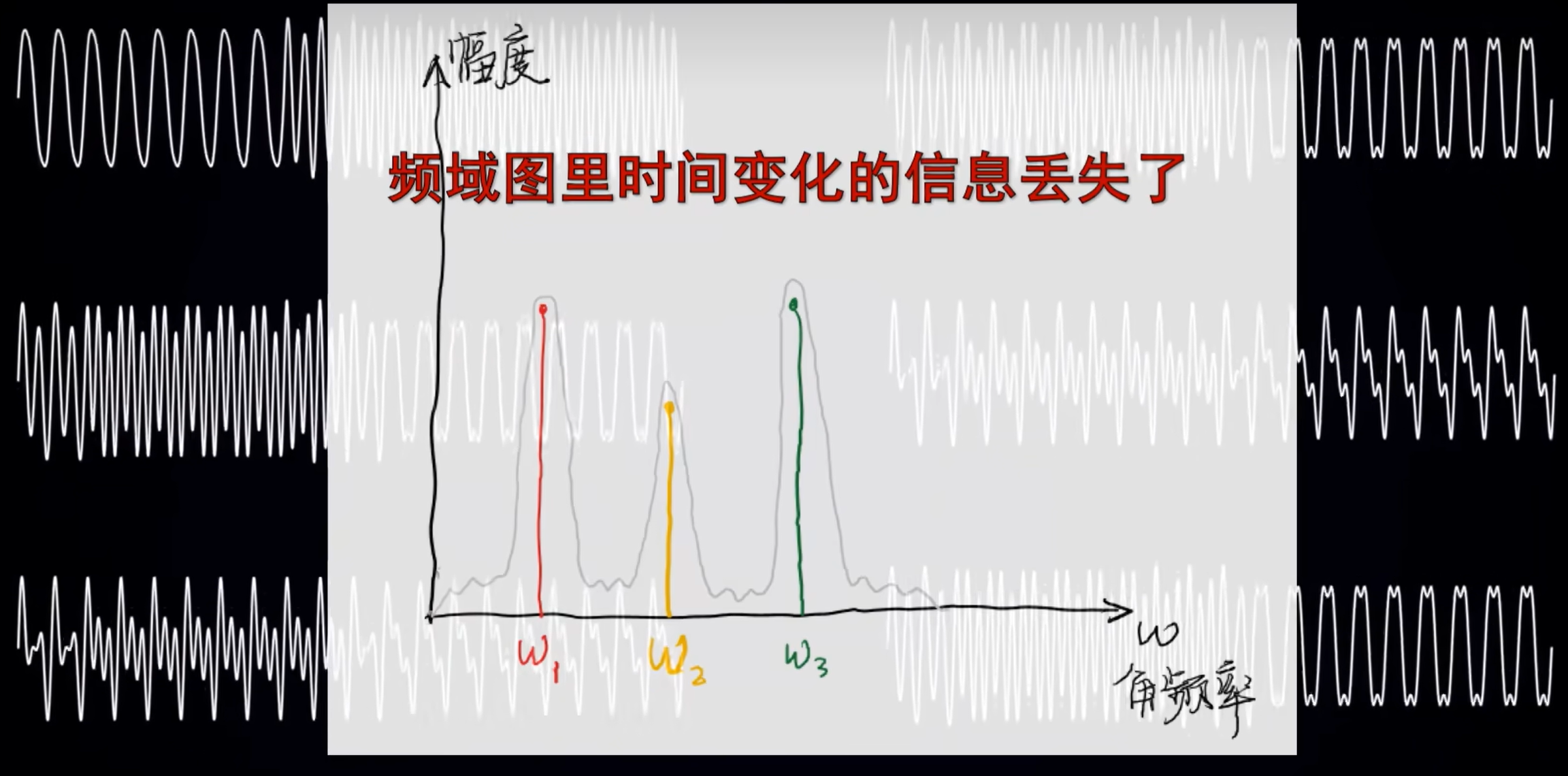
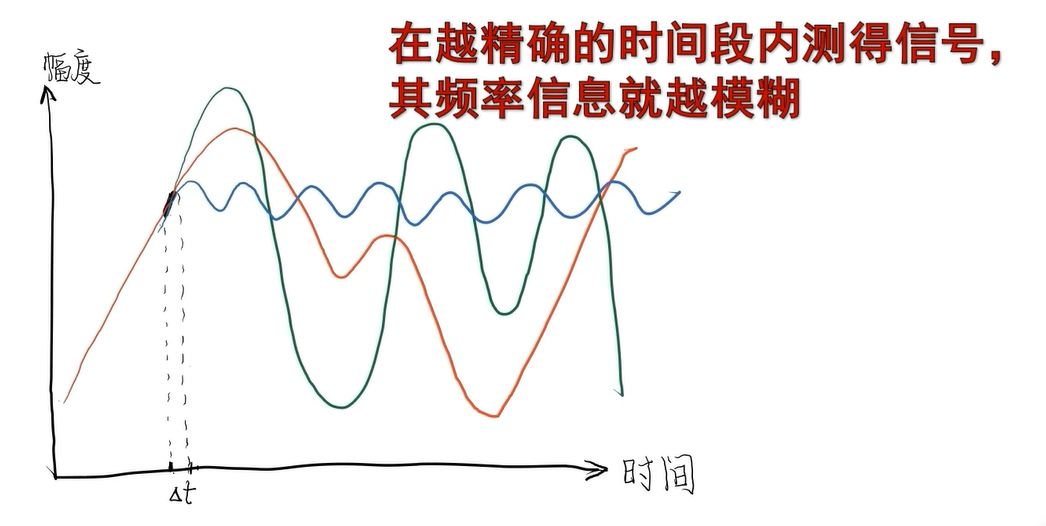
同样，在越精确（越窄）的一段时间内得到一段精确信号，在频率上能得到的信息就越模糊。

——傅里叶变化的不确定性原理。

理解：频率指的是一秒内完成几个周期循环，不给信号时间让它振完一个周期，频率就只能靠估了。

类似于量子力学领域海森堡的不确定性原理：微观粒子的位置和动量不能同时准确地获得。

从数学上看，这些不确定性原理（测不准原理）是一回事——是事物本身的性质，和测量工具的精度无关。

1.4 傅里叶变换的由来

1.4.1 傅里叶级数的起源

19世纪法国天才数学家、物理学家傅里叶在他的著作《热的解析理论》一书中提出：任何周期函数都可以分解成一个三角级数。

傅里叶在研究固体热传导的时候，提出了傅里叶级数的雏形……

2 拉普拉斯变换

发散函数不太好求傅里叶变换，可以先乘上一个收敛函数e^-ax，再求傅里叶变换。

拉普拉斯变化的公式，可以看到和点乘的积分形式特别相似：

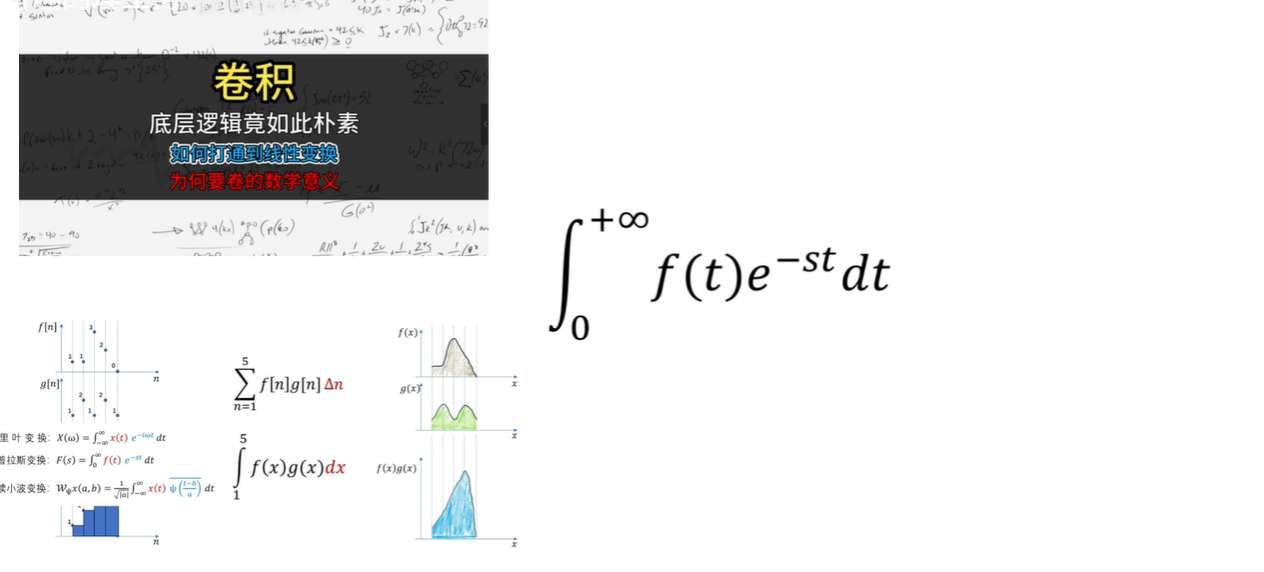
拉普拉斯的底层原理也是点乘：

• 我们使用一个东西去与目标函数进行点乘，目的就是想方设法去把这个目标函数的信息给榨取出来。

2.1 拉普拉斯变换想从原函数中榨取什么信息

我们这个世界遵循熵增法则，世界万物的有序度一定是在衰减的，所有的自然事物都会在时间的流逝中慢慢消磨自己。

这些现象都对应到一个词——衰减。

所以研究衰减的规律，就很重要了。

学傅里叶变换时知道，一条复杂的函数曲线可以分解成无数个不同频率的简单正余弦函数的线性叠加。

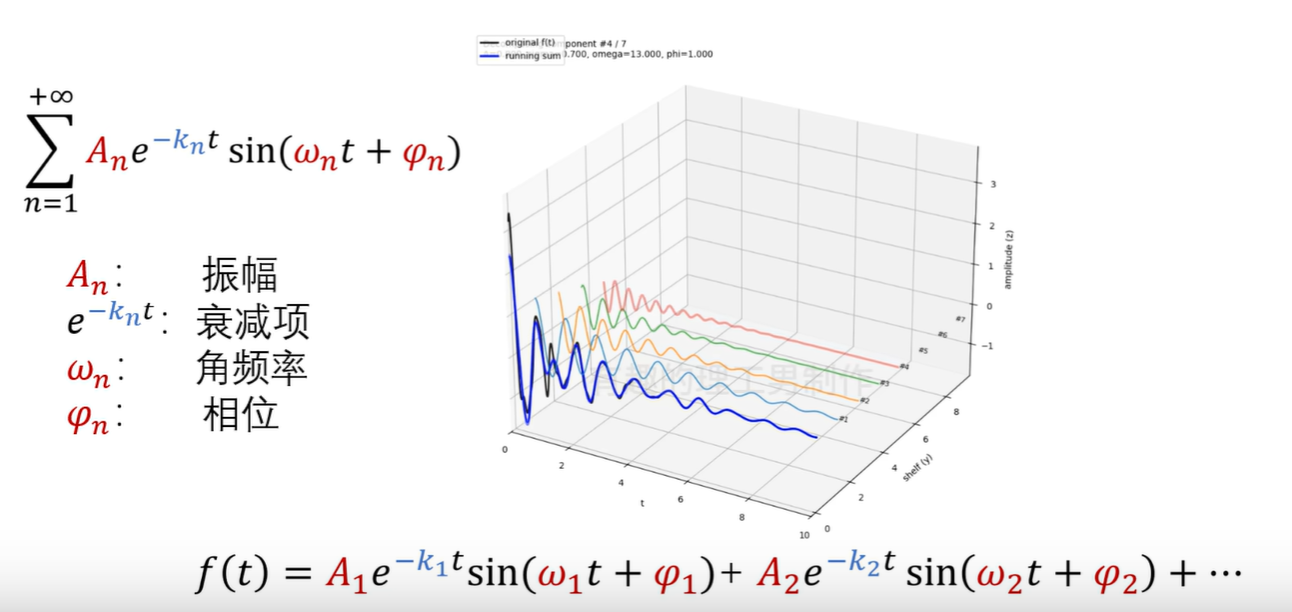
以上是一条衰减曲线，分解成不同成分带着不同程度的衰减的正弦函数的线性组合，有些频率成分衰减得慢、有些频率成分衰减得快。

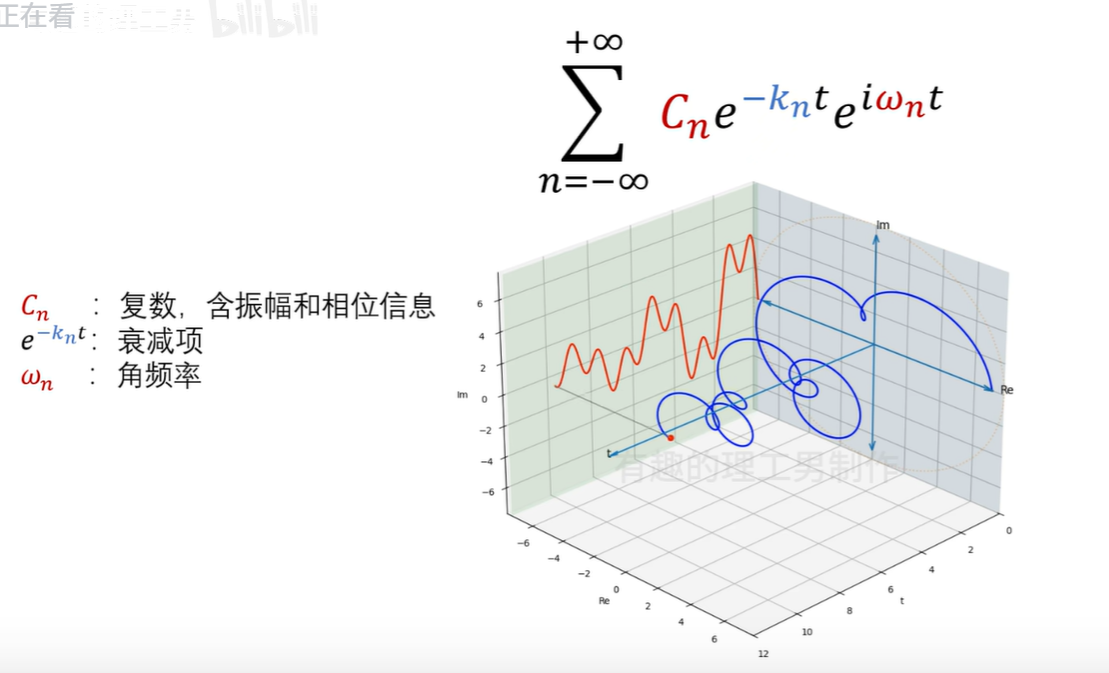
至此我们得知描述衰减现象有两个最重要的参数：频率ωn、衰减系数-kn。

如何利用拉普拉斯变换榨取出：频率ωn、衰减系数-kn这两个信息呢？？？

---

回顾傅里叶变换

带入每个ω，就可以得到每个频率下振荡的振幅，即每个频率的振荡强度（正比于A^2）。

而且这个复函数包含相位信息，即每个频率下的振荡是从什么时候开始的也知道了。

---

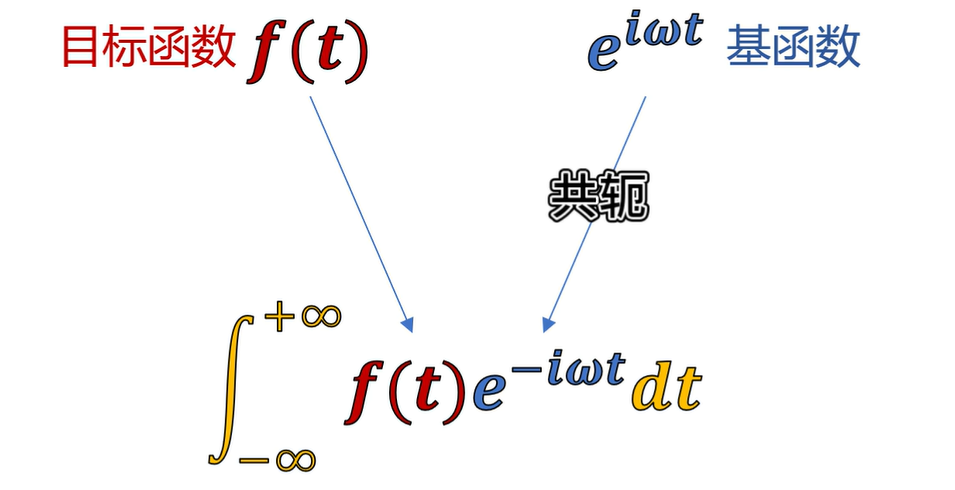
在复数域，和另一个函数点乘，应该是使用自己的共轭去和别人相乘，再求积分。

---

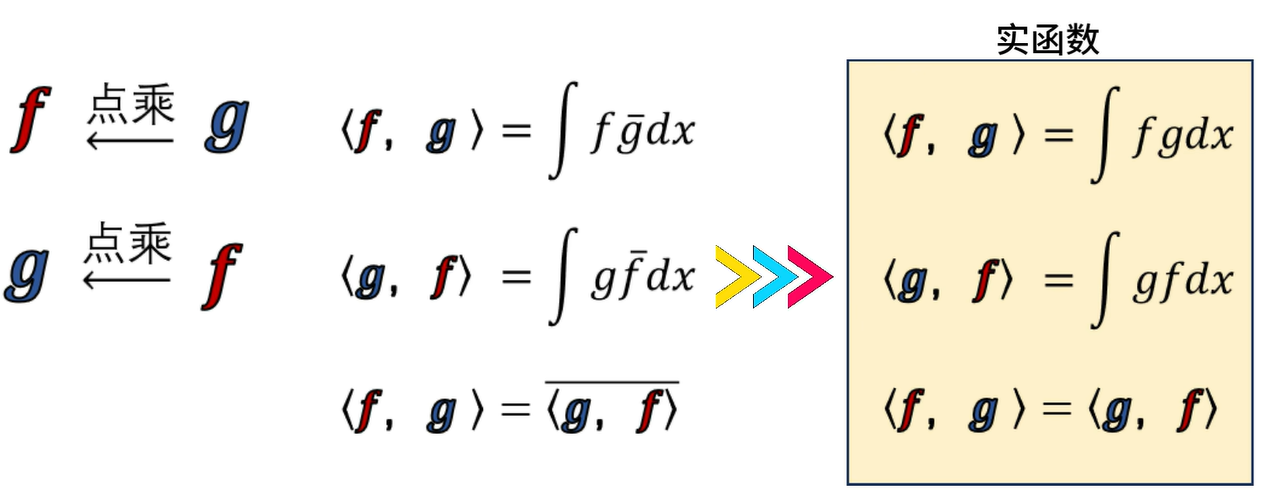
想得到衰减函数（振幅衰减，中心频率不变）也还是可以使用e^iωt这个基去点乘得到

但是这样得到的频率信息，和傅里叶变换还是有很大的差别，因为傅里叶变换可以得到这个频率下的能力占比，但是现在拉普拉斯点乘得到的东西还会受制于衰减系数，衰减地快一些，能量就会低一些。

所以还是需要找到衰减系数——方法：做标记。

衰减的形象可以描述为一个本不收敛的函数被另一个衰减的函数给摁了下去，如果想办法把这个衰减的函数的干掉，剩下一个发散的函数积分——标记极点。

用傅里叶变换的手段，搭配抵消衰减的指数函数，取获取频率和衰减的信息。

当衰减刚好抵消，且频率完全共振的时候，积分值无穷大，而其他位置就收敛。那么只要找到无穷大的地方，看一下它抵消衰减的衰减系数以及频率，那我们要研究衰减现象最重要的两个东西就知道了。

那就有：

那我们盯着无限大的地方，就可以找到对应的衰减系数和频率了。

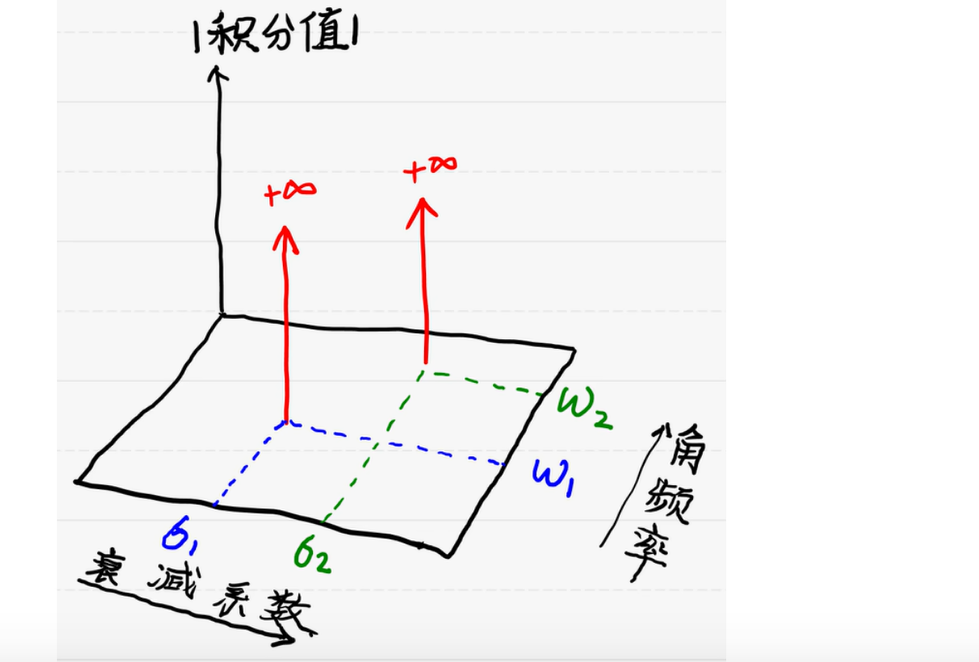
从公式本身，强化一下对作标记的理解，看到结果是一个关于σ、ω的二元函数。

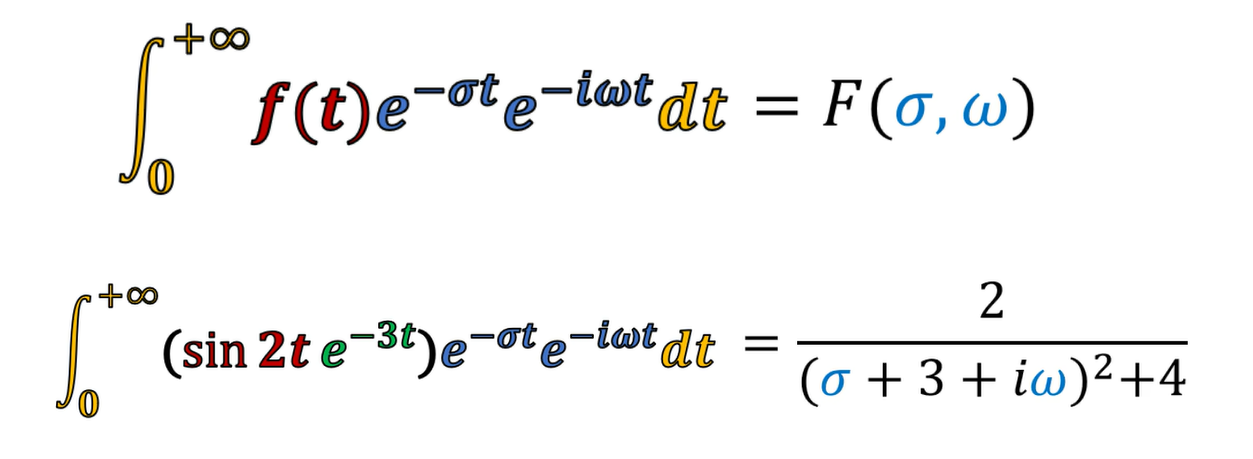
当σ = -3、ω = ±2的位置，结果的模长是无穷大的。

这两个位置正好对应原函数中的振荡频率、衰减系数。

---

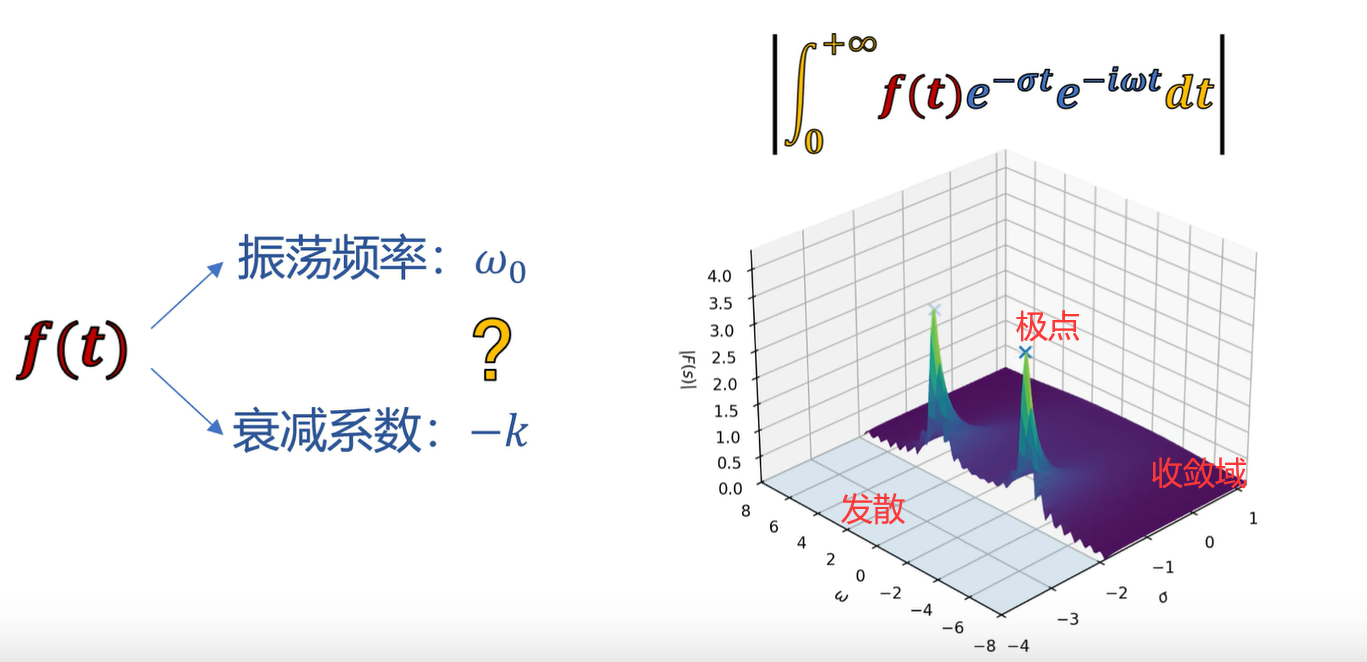
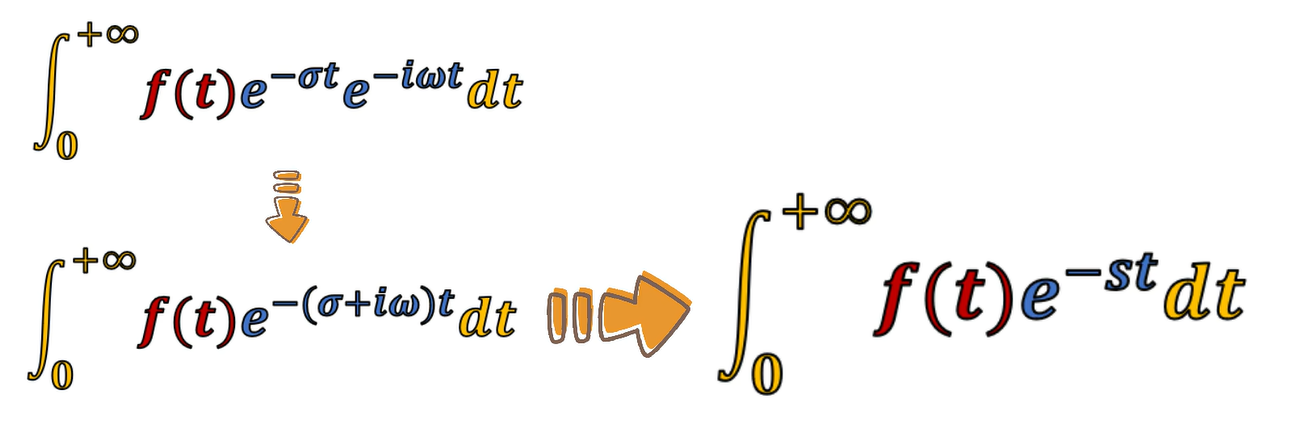
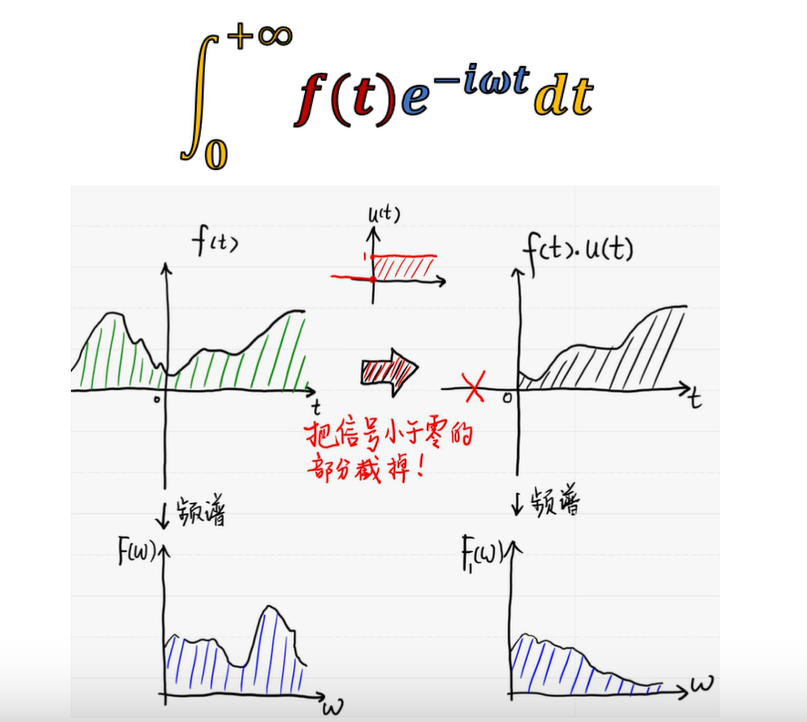
σ = 0时的（单边）拉普拉斯变换就是单边傅里叶变换。

σ ≠ 0的拉普拉斯变换也可以看作傅里叶变换——加权傅里叶变换：

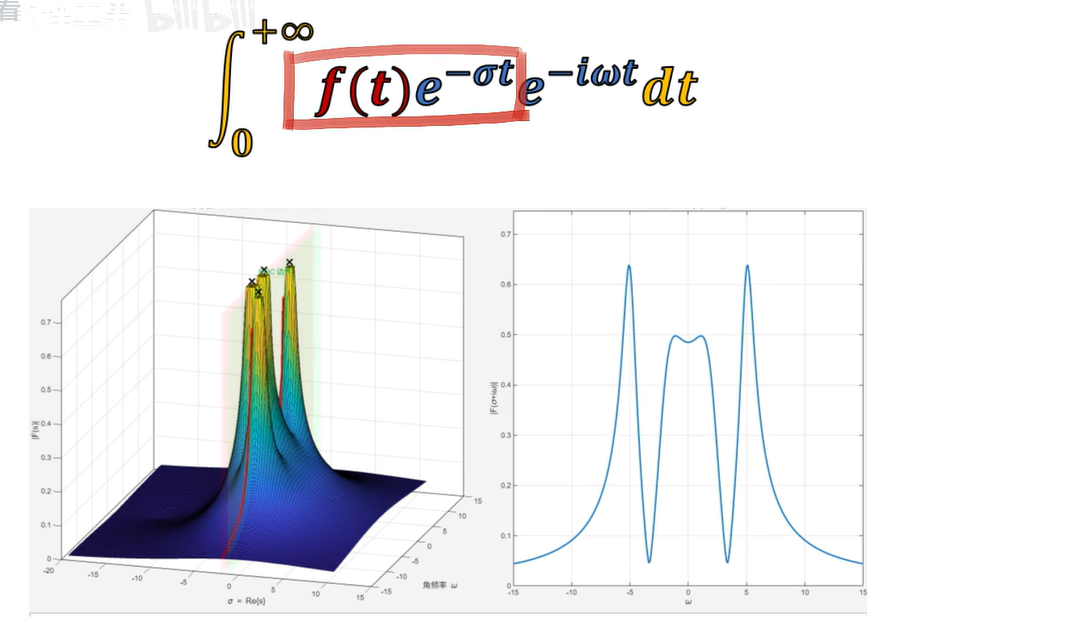
傅里叶变换重视基函数的归一化，这样子得到的频率和能力的占比才准确。

拉普拉斯变换作为带权傅里叶变换，原函数的能量会被这个权值给影响，它也就失去了能量占比的衡量的意义了，它的意义更多是在于帮助我们找到系统的瞬态——振荡的频率成分对应了多少的衰减。

这样子就算原函数中的频率成分不是衰减的，而是放大的，拉普拉斯变换也能处理，e^-σt不仅可以用来抵消衰减，也能够用来抵消放大。