深入理解栈与队列——从原理理解到实战应用

一、引言

二、栈（Stack）

2.1 栈的基本概念

2.2 栈的使用

2.3 栈的模拟实现

2.4 栈的实战应用

2.4.1 括号匹配

2.4.2 逆波兰表达式求值

2.4.3 出栈入栈次序匹配

2.4.4 最小栈

三、队列（Queue）

3.1 队列的基本概念

3.2 队列的使用

3.3 队列的模拟实现

3.4 队列的实战应用

3.4.1 设计实现循环队列

四、常见面试题与实战应用

4.1 用队列实现栈

4.2 用栈实现队列

五、总结

一、引言

数据结构是编程的基石，无论是算法设计还是系统开发，都离不开对数据结构的深入理解。栈和队列作为两种最基础的线性数据结构，广泛应用于各种场景中。本文将系统性地介绍栈和队列的概念、实现方式以及实际应用，帮助读者建立完整的知识体系。

二、栈（Stack）

2.1 栈的基本概念

栈是一种遵循先进后出（FILO，First In Last Out）原则的线性数据结构，只允许在栈顶进行入栈（压栈）和出栈操作。

拿生活中的一些现象举例子：比如超市里盘子售卖区的一摞一摞盘子，我们想要新增盘子只能放在最顶部，同样地，拿出盘子也只能在最顶部拿。

2.2 栈的使用

在Java内置的Stack类中，提供了以下操作方法：

public void push(int data)	入栈/压栈，即增加新元素
public int pop()	出栈，即删除栈顶的元素并返回该元素
public int peek()	获取栈顶元素并返回，不删除
public boolean empty()	判断栈是否为空
public int size()	获取栈的大小

具体使用示例如下：

import java.util.Stack;public class StackExample {public static void main(String[] args) {Stack<Integer> stack = new Stack<>();// 压栈操作stack.push(1);stack.push(2);stack.push(3);// 查看栈顶元素System.out.println("栈顶元素: " + stack.peek()); // 输出 3// 出栈操作System.out.println("出栈: " + stack.pop()); // 输出 3System.out.println("出栈: " + stack.pop()); // 输出 2// 判断栈是否为空System.out.println("栈是否为空: " + stack.empty()); // 输出 false// 获取栈的大小System.out.println("栈的大小: " + stack.size());   // 输出 1}
}

2.3 栈的模拟实现

在模拟实现栈时，我们可以选用数组也可以选用链表：用数组实现的栈叫顺序栈；用链表实现的栈叫链式栈。

我们先编写一个 MyStack 类如下：

public class MyStack {// 顺序栈public int[] arr;public int usedSize;           //用于记录栈的元素个数public MyStack(int[] arr) {this.arr = new int[10];    //暂定长度为10}// 链式栈（单向）static class ListNode {public int val;public ListNode next;public ListNode(int val) {this.val = val;}}public ListNode head;public int usedSize;           //用于记录栈的元素个数// 链式栈（双向）static class ListNode {public int val;public ListNode prev;public ListNode next;public ListNode(int val) {this.val = val;}}public ListNode head;public ListNode tail;public int usedSize;           //用于记录栈的元素个数
}

接下来我们来实现 push方法，思路很简单，我们只需要在 usedSize 位置增加新元素就可以了，但是要注意栈满了的时候，需要扩容。

顺序栈实现如下：

public void push(int data) {if (empty()) {this.arr = Arrays.copyOf(this.arr,2*this.arr.length);    //扩容为原长度的2倍}arr[usedSize] = data;usedSize++;
}

单向链式栈实现思路：使用头插法入栈，时间复杂度是O(1)

public void push(int data) {// 头插法入栈ListNode toAdd = new ListNode(data);toAdd.next = head;head = toAdd;usedSize++;
}

双向链式栈实现方式可以头插也可以尾插。

public void push(int data) {// 头插法ListNode toAdd = new ListNode(data);toAdd.next = head;head.prev = toAdd;head = head.prev;usedSize++;
}public void push(int data) {// 尾插法ListNode toAdd = new ListNode(data);tail.next = toAdd;toAdd.prev = tail;tail = tail.next;usedSize++;
}

然后是 pop方法，我们只需要将 usedSize 的个数减一即可。虽然元素在数组中仍然存在，但是不需要担心，等到下次增加元素时，该元素将被覆盖。

顺序栈实现如下：

public int pop() {if (empty()) {throw new EmptyStackException("This stack is empty!");}usedSize--;return this.arr[usedSize];
}

单向链式栈：我们可以使用头删法，每次删除并返回链表的第一个节点

public int pop() {if (empty()) {throw new EmptyStackException("This stack is empty!");}int val = head.val;head = head.next;usedSize--;return val;
}

双向链式栈：与单向链式栈不同的是，我们需要把第二个节点的 prev 置空

public int pop() {if (empty()) {throw new EmptyStackException("This stack is empty!");}int val = head.val;head = head.next;head.prev = null;usedSize--;return val;
}

其中的异常编写如下：

public class StackEmptyException extends RuntimeException {public StackEmptyException() {super();}public StackEmptyException(String message) {super(message);}
}

peek方法十分简单，只需要返回 usedSize - 1 位置的元素即可，但是注意要判断栈是否为空。

顺序栈实现如下：

public int peek() {if (empty()) {throw new EmptyStackException("This stack is empty!");}return this.arr[usedSize-1];
}

单/双向链式栈：直接返回链表第一个节点的 val 即可

public int peek() {if (empty()) {throw new EmptyStackException("This stack is empty!");}return head.val;
}

empty方法，只需判断 usedSize 是否等于数组的长度即可。

顺序栈实现如下：

public boolean empty() {return usedSize == this.arr.length;
}

单/双向链式栈：判断指向链表第一个节点的引用是否为空即可

public boolean empty() {if (head == null) return true;return false;
}

最简单的是 size方法，只需要返回 usedSize 即可：

public int size() {return this.usedSize;
}

对于单/双链式栈来说，需要遍历整个栈：

public int size() {ListNode cur = head;int count = 0;while (cur != null) {count++;cur = cur.next;}return count;
}

2.4 栈的实战应用

栈相关的面试题：

2.4.1 括号匹配

算法实现思路：

遍历字符串，如果是左括号，就放入栈中；如果是右括号，就获取栈顶元素并进行匹配
情况一：当栈为空并且字符串遍历完成，左右括号都匹配成功时，返回true；情况二：当左右括号匹配失败时，返回false；情况三：当字符串遍历完成但是栈不为空时，表示左括号多余，返回false；情况四：当字符串未遍历完成但是栈已经空了，表示右括号多余，返回false。
注意：当遍历字符串发现字符是右括号时，在匹配前必须先检查栈是否为空：若不为空才进行匹配；若为空则是第四种情况

具体实现如下：

public boolean isValid(String s) {Stack<Character> stack = new Stack<>();for (int i = 0; i < s.length(); i++) {char ch = s.charAt(i);if (ch=='(' || ch=='[' || ch=='{') {stack.push(ch);} else {    // 此时 ch 是右括号if (stack.empty()) {       // 栈已空，右括号多余return false;}char leftCh = stack.peek();if ((leftCh=='(' && ch==')')|| (leftCh=='[' && ch==']')|| (leftCh=='{' && ch=='}')) {     // 匹配成功stack.pop();} else {               // 匹配失败return false;}}}if (!stack.empty()) {       // 栈不为空但字符串已经遍历完成，左括号多余return false;}return true;
}

2.4.2 逆波兰表达式求值

算法实现思路：

遍历，遇到数字就放入栈，遇到运算符就取出两个栈顶数字并进行计算（第一个取出的数字作为右操作数，第二个作为左操作数），将计算结果放入栈
当遍历完成后，栈中所存的元素就是该表达式的最终结果

中缀表达式转后缀表达式（逆波兰表达式）的计算方法：

先判断中缀表达式的优先级，然后按照优先级依次在算式外部添加括号
全部添加完成后，从左至右依次将运算符移至括号后面
例：中缀表达式 a + b * c + ( d * e + f ) * g
首先划分优先级：
单项式( d * e ) ——> 多项式( ( d * e ) + f ) ——> 多项式( ( d * e ) + f ) * g ) ——> 单项式( b * c ) ——> 多项式( a + ( b * c ) ) ——> 多项式（ ( a + ( b * c ) ) + ( ( d * e ) + f ) * g ) ）
然后按照优先级先后把运算符全部移到括号后面：
( ( a + ( b * c ) ) + ( ( ( d * e ) + f ) * g ) ) ——> ( ( a ( b c ) * ) + ( ( ( d e ) * f ) + g ) * ) +
去掉所有的括号最终结果就是:
a b c * + d e * f + g * +

具体实现如下：

public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for (String s : tokens) {if (s.equals("+")|| s.equals("-")|| s.equals("*")|| s.equals("/")) {    // 是运算符int v2 = stack.pop();   // 右操作符int v1 = stack.pop();   // 左操作符switch (s) {case "+":stack.push(v1+v2);break;case "-":stack.push(v1-v2);break;case "*":stack.push(v1*v2);break;case "/":stack.push(v1/v2);break;}} else {            // 是数字int val = Integer.parseInt(s);  // 转换为整型stack.push(val);}}return stack.pop();
}

2.4.3 出栈入栈次序匹配

算法实现思路：

遍历pushV数组并入栈，每次入栈一个元素之后拿栈顶元素与popV数组中的 j 位置的元素进行比较是否相等：若一样，就可以出栈；否则，继续遍历pushV数组、入栈
一旦有一个元素相等，后面的所有元素均相等
当栈为空或者popV数组和pushV数组遍历完成时，返回true

具体实现如下：

public boolean isPopOrder (int[] pushV, int[] popV) {Stack<Integer> stack = new Stack<>();int j = 0;for (int i = 0; i < pushV.length; i++) {stack.push(pushV[i]);while (j < popV.length&& !stack.isEmpty()&& stack.peek() == popV[j]) {stack.pop();j++;}}return stack.isEmpty();
}

2.4.4 最小栈

算法实现思路：

使用两个栈，一个普通栈（stack）存放所有的数据，一个最小栈（minStack）用于存放当前 stack 所存元素的最小值
入栈：当第一个元素放入 stack ，且 minStack 为空时，minStack 也要放。接下来 stack 存放元素后，都要与 minStack 的栈顶元素进行大小比较：若比栈顶元素小，就放入 minStack（注意：若与栈顶元素相等，也要放入）；否则不放入
出栈：当普通栈出一个元素时，判断一下最小栈是否也有相同的元素：若有就出；否则不出

具体实现如下：

public class MinStack {Stack<Integer> stack;Stack<Integer> minStack;public MinStack() {stack = new Stack<>();minStack = new Stack<>();}public void push(int val) {stack.push(val);if (minStack.empty()) {minStack.push(val);} else {if (val <= minStack.peek()) {minStack.push(val);}}}public void pop() {if (stack.empty()) return;int val = stack.pop();if (minStack.peek() == val) {minStack.pop();}}public int top() {if (stack.empty()) return -1;return stack.peek();}public int getMin() {if (stack.empty()) return -1;return minStack.peek();}
}

三、队列（Queue）

3.1 队列的基本概念

队列是一种遵循先进先出（FIFO, First In First Out）原则的线性数据结构。只允许在队尾进行插入操作，在队头进行删除操作。

现实生活中的队列例子：

排队购票：先来的人先得到服务
打印机任务队列：先提交的打印任务先执行

3.2 队列的使用

在Java内置的Queue类中，提供了以下操作方法：

public void offer(int data)	入队，即增加新元素
public int poll()	出队，即删除队头元素并返回该元素
public int peek()	获取队头元素并返回，不删除
public boolean isEmpty()	判断队列是否为空
public int size()	获取队列的大小

具体使用示例如下：

import java.util.LinkedList;
import java.util.Queue;public class QueueExample {public static void main(String[] args) {Queue<Integer> queue = new LinkedList<>();// 入队操作queue.offer(1);queue.offer(2);queue.offer(3);// 查看队头元素System.out.println("队头元素: " + queue.peek()); // 输出 1// 出队操作System.out.println("出队: " + queue.poll()); // 输出 1System.out.println("出队: " + queue.poll()); // 输出 2// 判断队列是否为空System.out.println("队列是否为空: " + queue.isEmpty()); // 输出 false// 获取队列的元素个数System.out.println("队列的长度: " + queue.size()); // 输出 1}
}

3.3 队列的模拟实现

由于Java的内置队列 Queue 是采用双向链表实现的，我们这里也使用双向链表。各个方法的实现思路与栈的方法的实现思路差不多，此处不再过多阐述。

具体实现如下：

public class MyQueue {static class ListNode {public int val;public ListNode prev;public ListNode next;public ListNode(int val) {this.val = val;}}public ListNode first;public ListNode last;public int usedSize;public void offer(int data) {   // 尾插ListNode toAdd = new ListNode(data);if(first == null) {first = last = toAdd;return;}last.next = toAdd;toAdd.prev = last;last = last.next;usedSize++;}public int poll() {    // 头删if(first == null) {return -1;}int v = first.val;first = first.next;if (first != null) {first.prev = null;}usedSize--;return v;}public int peek() {     // 获取队头的值if(first == null) {return -1;}return first.val;}public int size() {    // 获取队列的大小return usedSize;}
}

3.4 队列的实战应用

3.4.1 设计实现循环队列

我们把一个数组卷起来呈圆形，以这样的结构来实现的队列称为循环队列。

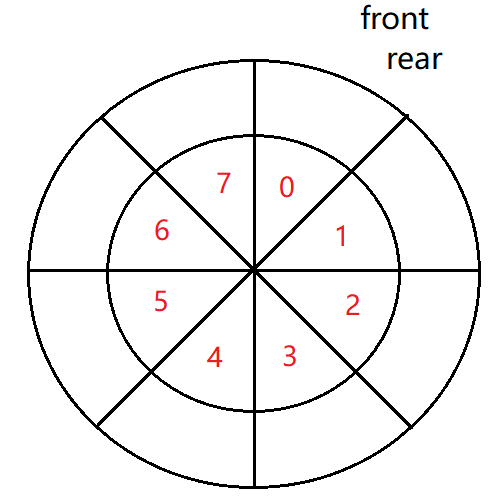
当两个引用 front 和 rear 指向同一个位置（即 front == rear）时，该队列为空。

它的方法如下：

public boolean enQueue(int value)	入队，即增加新元素
public boolean deQueue()	出队，即删除队头元素并返回该元素
public int Front()	获取队头元素并返回
public int Rear()	获取队尾元素并返回
public boolean isEmpty()	判断队列是否为空
public boolean isFull()	判断队列空间是否已满

算法实现思路：

如何判断队列为空/队列已满？：当 front == rear
怎么区分为空还是为满？：1.定义 usedSize；2.空出最后一个位置；3.添加一个布尔类型的变量作为标记
怎么做到循环遍历队列？即怎么让 rear 从下标为7的位置走到下标为0的位置呢？：用公式( rear + 1 ) % array.length判断 rear 的下一个是否 front
入队列、出队列、返回队头元素、返回队尾元素（需要判断 rear）

具体实现如下：

class MyCircularQueue {    // 这里采用的是第二种方法区分为空还是为满public int front;public int rear;public int[] elem;public MyCircularQueue(int k) {this.elem = new int[k+1];}public boolean enQueue(int value) {    // 入队列if (isFull()) {return false;}elem[rear] = value;rear = (rear+1)%elem.length;return true;}public boolean deQueue() {    // 出队列if (isEmpty()) {return false;}front = (front+1)%elem.length;return true;}public int Front() {    // 获取队头元素if (isEmpty()) {return -1;}return elem[front];}public int Rear() {    // 获取队尾元素if (isEmpty()) {return -1;}int pos = (rear==0) ? elem.length-1 : rear-1;return elem[pos];}public boolean isEmpty() {return rear == front;}public boolean isFull() {return (rear+1)%elem.length == front;}
}

四、常见面试题与实战应用

4.1 用队列实现栈

算法实现思路（使用两个队列）：

模拟的入栈操作：将入栈的元素放入不为空的队列中；
第一次入栈默认放入qu1中，接下来判断哪个队列不为空就放入哪个队列中：if...else if...else
模拟的出栈操作：把不为空的队列中的除要出栈的元素之外的（size-1）所有元素放入另一个队列当中，再出队列即可；先判断栈是否为空，再判断哪个队列不为空就出哪个队列
模拟的获取栈顶元素操作：在出栈操作的基础下（把全部元素都出），加一个变量存储出队列的元素，当最后一个出队列的元素存储后，该值就是模拟的栈顶元素
两个队列交替工作

具体实现如下：

public class MyStack {Queue<Integer> qu1;Queue<Integer> qu2;public MyStack() {qu1 = new LinkedList<>();qu2 = new LinkedList<>();}public void push(int x) {if (!qu1.isEmpty()) {qu1.offer(x);} else if (!qu2.isEmpty()) {qu2.offer(x);} else {qu1.offer(x);}}public int pop() {if (empty()) {return -1;}if (!qu1.isEmpty()) {int size = qu1.size();for (int i = 0; i < size-1; i++) {qu2.offer(qu1.poll());}return qu1.poll();} else {int size = qu2.size();for (int i = 0; i < size-1; i++) {qu1.offer(qu2.poll());}return qu2.poll();}}public int top() {if (empty()) {return -1;}if (!qu1.isEmpty()) {int size = qu1.size();int val = 0;for (int i = 0; i < size; i++) {val = qu1.poll();qu2.offer(val);}return val;} else {int size = qu2.size();int val = 0;for (int i = 0; i < size; i++) {val = qu2.poll();qu1.offer(val);}return val;}}public boolean empty() {return qu1.isEmpty() && qu2.isEmpty();}
}

4.2 用栈实现队列

算法实现思路（使用两个栈）：

指定一个栈用来入队列，一个栈用来出队列
模拟的入队列操作：放入指定的入队列栈中即可
模拟的出队列操作：先判断出队列栈是否为空？：若为空，将入队列栈中的元素放入出队列栈中，再出栈即可；否则直接出栈
模拟的获取队头元素操作：在出队列操作下，直接peek出队列栈的栈顶元素即可

具体实现如下：

public class MyQueue {Stack<Integer> st1;Stack<Integer> st2;public MyQueue() {st1 = new Stack<>();st2 = new Stack<>();}public void push(int x) {st1.push(x);}public int pop() {if (empty()) {return -1;}if (st2.isEmpty()) {while (!st1.isEmpty()) {st2.push(st1.pop());}}return st2.pop();}public int peek() {if (empty()) {return -1;}if (st2.isEmpty()) {while (!st1.isEmpty()) {st2.push(st1.pop());}}return st2.peek();}public boolean empty() {return st1.isEmpty() && st2.isEmpty();}
}