Unity-NavMesh详解-其一

今天我们来详细地探究一下Unity的NavMesh这一性能强大的组件：

NavMesh基本使用

NavMesh简单地说本质上是一个自动寻路的AI组件，我们首先来学习基本的使用。

画面中我已经添加好了地面，目标，障碍物以及玩家四个要素。

注意我们要进行NavMesh的一些前提工作：

在所有我们想要加入NavMesh网格导航的场景元素的static处选择Navigation Static。

然后在window->ai处可以看到Navigation。

打开后如图所示：

可以看到有四个部分，我们一部分一部分地来看：

Agent，我们可以理解为导航代理，简单地说，如果我们借助NavMesh实现自动寻路，那么所有有自动寻路功能的对象都需要挂载NavMeshAgent，这个Agent定义的东西包括挂载对象在NavMesh网格中的半径、高度、最大可跨越的台阶高度(Step Height)、最大坡度（对于这个对象而言，超过这个坡度的网格被视作不可到达），我们还可以为这个代理命名。

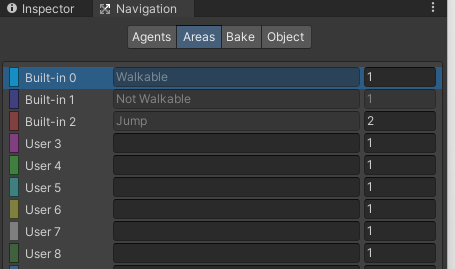
Areas，我们可以理解为导航的区域，因为NavMesh的底层是启发式算法，我们需要预先设定好各个不同区域的移动成本(cost)，图中的不同索引对应的就是不同区域的移动成本（0为可行走，1为不可行走）。

Bake，也就是烘焙。烘焙决定了我们会如何去根据场景中想要被NavMesh使用的具体情况来生成网格。

在这里我们可能要插入一下关于NavMesh的使用原理：

我们首先将场景中的设置为Navigation Static的物体的三角网格转换为体素（立方体小格子），然后过滤掉不可行走的区域（根据Bake中设定的参数如最大坡度最大台阶高度等），生成一个高度场（此时在XZ平面是一个个大小相等的格子，而在Y轴则是一个个高度值）；然后我们将相邻的体素合并成连续的可行走区域，之后我们再将体素的边界转化为一个个凹多边形（因为很多复杂的情况可行走区域只能转换成凹多边形），然后再将凹多边形转换为凸多边形（方便进行路径搜索），凸多边形最后会变成点和线的集合，也就是可行走区域最后会转化成一个图结构，在图上我们就可以去使用寻路算法了。

而Bake本质上就是我们去执行NavMesh体素化时的一些考虑参数，比如我们可以看见的Agent的半径、高度等，值得注意的是，我们这里的Agent 参数和之前Agent的Radius的参数意义并不相同：比如这里的Agent Radius代表的是Agent与其他物体（也包括其他Agent）之间的最小距离，换句话说就是防止两个物体离得太近。除此之外还有生成离网链接等功能（离网链接即一些特殊情况下的路线）

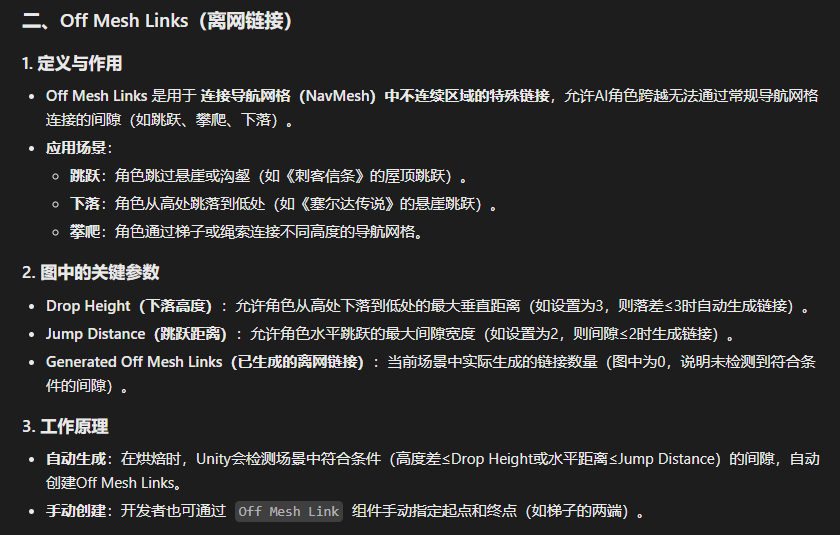
这个模块就比较简单了，基本都是前面我们所说的内容。

现在我们只需要按下Bake键，就可以看到烘焙后的场景了：

可以看到有一层绿色笼罩在地面上，现在我们要做的是去实现一个基本的导航功能。

我们在Player身上挂载这个Nav Mesh Agent:是的，就是我们之前的Agent，可以看到我们的Agent Type就是我们之前定义的Humanoid，这里还有一些其他的参数如速度、角速度等。

有了Agent我们就可以导航了，不过我们还需要一个脚本来具体控制这个Player：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.AI;public class PlayerControl : MonoBehaviour
{public NavMeshAgent nav; //获取导航网格代理组件，通过此组件来告知AI目标public Transform target; //目标的位置private void Update(){nav.SetDestination(target.position); //每帧更新目标位置}}

填好参数之后，运行就可以看到：运行前：

运行后：

那么我们的基本的NavMesh就使用成功了。

一些其他的基本的Unity的NavMesh的内容大家可以在这里找到，这个博主写的更多是一些具体应用的方面，大家可以在这里查缺补漏。详解Unity中的Nav Mesh|导航寻路系统（一）_navmesh-CSDN博客

Recast Navigation

Unity的NavMesh的底层其实是基于我们的Recast Navigation实现的，这里有大神的帖子：

Recast Navigation源码分析：导航网格Navmesh的生成原理 - 知乎 (zhihu.com)

RecastNavigation 是一个的导航寻路工具集，它包括了几个子集：

所以我们如果想要理解Recast Navigation，就只需要搞明白三件事情：怎么根据输入生成导航网格、怎么在导航网格上自动寻路、怎么针对一群人自动寻路。

如何生成导航网格？

接下来让我们来一个一个过程地展开介绍：

体素化：

我们可以把像素看作2D平面的最小单位，那么体素就是3D空间内的最小单位。在生成导航网格的最开始，我们把3D空间中的物体变成一个个体素，将基于边界的表现形式（例如：多边形模型，曲面等）转换成为体积的表现形式（例如：体素块）并构建一个高度场。

高度场：

体素化之后的3D空间就像一个个用积木块拼凑出来的空间一样，而高度场则是将整个体素空间压缩成一个二维平面与一个高度值；体素化之后的体素空间内每一个体素都会包含高度信息，我们的高度场本质上只是把这个高度单独提出来作为信息之后再去除掉高度维度，这样就保留了高度信息的同时压缩了维度。

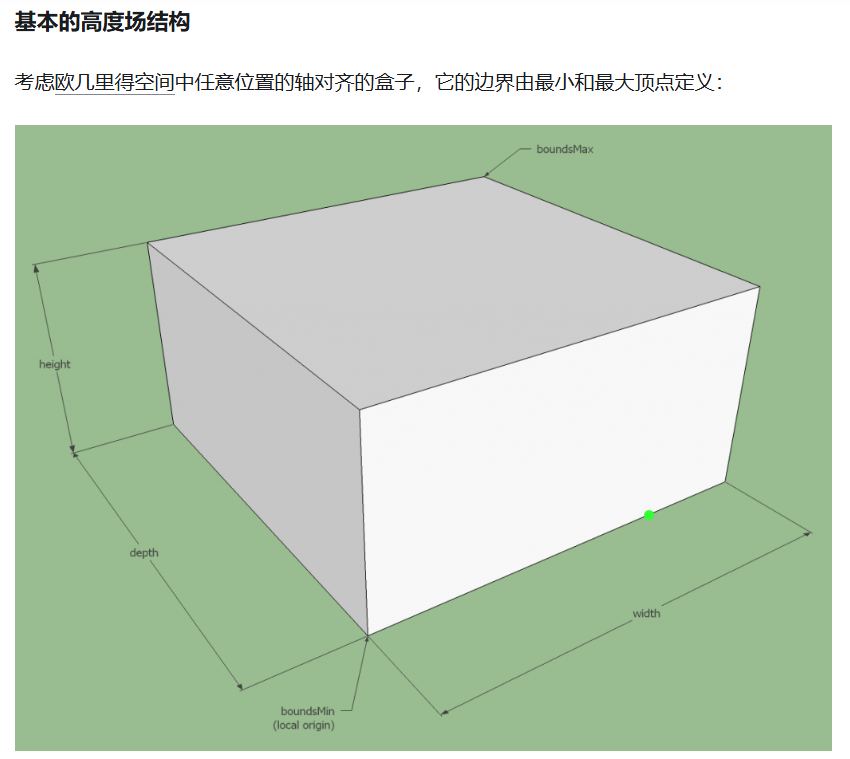
高度场是容纳所有体素格子的AABB包围盒，在可视化之后可以看到，我们会按照CellSize对这个包围盒进行XZ方向均匀的一个切割(关于CellSize，基本的原则是CellSize越大则计算开销越小，CellSize越小则越精细)，按照CellHeight接着对包围盒的高度进行均匀切割。切割后的一个个像素块就是一个个体素块，正常情况下我们用俯视的角度看到的应该是在XZ平面均匀分布的一个个方形，这些方形中存放着这个体素的高度区间的集合（Span），这个就是我们的高度场。

Span:

对于高度场中的一列体素，我们一般只会去关注他是否是“实心”的，有的话就代表这个体素的空间是有障碍的。我们会合并一列体素中的连续的实心体素，称为一个Span。

搜索邻居：

在NavMesh生成中，邻居搜索的核心目标是识别可行走区域的连通性，即判断哪些体素（或高度区间）可以相互连接形成连续的可行走表面。总的来说，搜索邻居的过程需要我们在高度场中的高度和平面综合考虑才可，我们会首先找到每一个体素块高度差值不超过预设值的体素块（预设值如Unity的最大台阶高度），然后再在XZ平面检查是否是邻接关系，最后判断是否是连续的可行走区域。

实体高度场：

体素化的最终目的就是为了创建一个实体的高度场，这个实体的高度场会表面具体哪里有障碍，同时也表明了连通的可行走区域。

需要注意的是，在之前我们的措辞中并没有说明关于从贴图转换到体积表达的具体过程其实就是把构成贴图的三角形转换成立方体，而这个过程中我们采取的策略是“保守体素化”：保证生成的体素将原来的几何图形全部包围。

生成实体高度场之后，我们就需要去考虑一些预设值的影响了，如最大坡度，最大可达台阶高度等，将实体高度场中不符合要求的部分过滤掉。

裁剪多边形表面是否可行走：

对于每一个Span，我们去判断该Span顶部体素的几何体的斜率是否低于可行走表面的最大坡度即可判断该表面是否可以通过：

光珊化三角形，添加span到实体高度场：

获取到具体可行走的多边形后，我们就要将这些多边形添加到实体高度场了，但是现在的问题是我们的多边形——其实是由一个个三维的三角形组成的——是一个非常难以处理的内容，我们不知道如何去把这个多边形放置在合适位置的高度场上。

如果你直接去处理多边形本身，那当然非常难以处理，误差可能很大。我们要做的是将这个多边形分割成一个个三角形，然后再将这一个个三角形转换成实体高度场需要的X-Z轴与高度信息，这里就牵扯到一个切割凸多边形的问题：我们的一个个三角形在X-Z轴的平面对应的体素格子里可能是一个个凸多边形。

从遍历凸多边形的每条边开始，通过检测每条边与分割线的空间关系来切割多边形：

若边的两个端点均位于分割线同侧，则保留该边，将其起点加入对应侧的新多边形顶点集；
若边跨越分割线（端点分居两侧），则计算交点并分割该边——交点同时加入两侧新多边形，起点按位置归属分配至具体子多边形；
遇端点落在分割线上时，将其同步标记为上下两个新多边形的共享顶点。
最终按序连接每侧的保留边、分割点和交点，生成两个边界连续的子凸多边形。

此流程通过沿X/Z轴方向每隔cellsize单位设置平行分割线（如图中五边形被网格线切割所示），将三角形表面递归分解为与网格列对齐的片段，继而通过取各片段顶点的最小Y值（体素下沿）和最大Y值（体素上沿），实现三维表面到体素化格子（x,z坐标+Y轴区间）的无损转换，为导航网格生成奠定数据基础。

上图为例，可以看到一个三维空间中的三角形，我们现在要做的事是把这个三角形转换成X-Z空间与高度信息的形式。

可以看到对于X-Z空间的一个体素格子来说，这个三角形的高度信息对应的就是这两个高度的体素格子与三角形的实际交点。

现在我们向实体高度场中添加span：

与多边形相交的网格列。
裁剪多边形的最小-最大高度范围（网格列被阻挡的部分）。

我们根据获得的最小最大高度范围来判断该span是否为可行走：

如果新span不与网格列中的任何已经存在的span相交，则会创建一个新span。如果新span与已经存在的span相交或被已经存在的span所包含，则合并这两个span。
当新span与已经存在的span合并时，必须评估生成的聚合span是否是可行走的。这个“可行走标志”只适用于span的顶部表面。如果设置了，就意味着span顶部表示多边形，该多边形有足够低的斜率是可行走的。
如果新span的顶部高于它正在合并到的span，则新span的可行走标志用于聚合span；如果新span的顶部低于它正在合并到的span，那么我们不关心新span的标志，新span的标志被丢弃。
如果新span的顶部与其合并到的span处于同一高度，则如果其中任意一个被认为是可行走的，聚合span就被标记为可行走。

一句话：看哪个span高，高的span能行走就走，否则就不能走。

这样我们的体素化过程就大体完成了：

体素化过程始于建立高度场这一基础数据结构，它将空间按配置的精度（cellSize、cellHeight）划分为网格，并在每个网格位置（x,z）存储称为 Span 的高度区间链表（每个Span记录下界 smin 和上界 smax）。通过分析输入三角面片，系统裁剪多边形表面并基于坡度参数（walkableSlopeAngle）初步判断其是否可行走。核心操作是 光栅化三角形：将每个三角形分割为与网格列对齐的凸多边形片段，计算其顶点Y值范围（即Span的smin/smax），并将这些携带可行走标记的Span添加到实体高度场中（处理Span重叠与合并）。最终生成的实体高度场完整记录了三维场景中所有实体（障碍）占据的空间及其表面的可行走属性。为准备后续区域生成，算法会对实体高度场进行搜索邻居操作：在垂直方向过滤不满足Agent高度（walkableHeight）的Span，并在水平方向检测满足可攀爬高度差（walkableClimb）的相邻Span连接关系，该步骤实质上是在转换数据为开放高度场（CompactHeightfield） 并预计算连通性，为导航网格的洪水填充区域划分奠定基础。

筛选可走表面

span有一个标志，指示其顶面是否被认为是可行走的。但是此标志仅根据与span相交的多边形的斜率来设置。现在是进行更多过滤的好时机。此过滤从某些span中删除可行走标志。

Recast Navigation中给出了三种过滤方法：

筛选低垂的可行走障碍

为了在低洼区域形成可走区域。比如楼梯，将不可走标记为可走。

算法比较简单：迭代每一列，从下往上遍历span，对于同列任意两个相邻的span1（下）和span2（上），当span1可走，并且span2不可走的时候，计算这两个span的上表面高度差Diff，如果Diff小于配置参数“walkableClimb”，则将span2设置为“可走”。

显然比较常见的场景就是从低向高的攀爬场景，只要两个span的高度差不大于参数就允许行走。

void rcFilterLowHangingWalkableObstacles(rcContext* ctx, const int walkableClimb, rcHeightfield& solid)
{rcAssert(ctx);rcScopedTimer timer(ctx, RC_TIMER_FILTER_LOW_OBSTACLES);const int w = solid.width;const int h = solid.height;for (int y = 0; y < h; ++y){for (int x = 0; x < w; ++x){rcSpan* ps = 0;bool previousWalkable = false;unsigned char previousArea = RC_NULL_AREA; for (rcSpan* s = solid.spans[x + y*w]; s; ps = s, s = s->next){const bool walkable = s->area != RC_NULL_AREA;  // 如果当前跨度不可行走，但其下方有可行走跨度，则将其上方的跨度也标记为可行走。if (!walkable && previousWalkable){if (rcAbs((int)s->smax - (int)ps->smax) <= walkableClimb)s->area = previousArea;}// Copy walkable flag so that it cannot propagate// past multiple non-walkable objects.previousWalkable = walkable;previousArea = s->area;}}}
}

过滤可行走的低高度区间

这个是同列相邻两区间之间距离的校验，保证最小可通过距离，可走变不可走。如果在span上方有太近的障碍物，那么span的顶面是不能穿越的。也就是说span的顶部与其上方span的底部至少有一个最小距离（最高的agent可以站在span上而不会与上方的障碍物发生碰撞）。想象一张桌子放在地板上，桌子下面的地板表面是平的，但由于桌子比较矮，不能在桌子底下行走，所以不能被认为是可穿越的（traversable）。

迭代每一列，从下往上遍历span，如果当前span不可走，直接跳过。
否则，计算当前span_B的上表面和其上相邻的span_A的下表面之间的高度差Diff。span_A不存在的话，高度差Diff设为无穷大。
如果“高度差Diff”小于“walkableHeight”，则将当前span的标识位置为“不可走”。

void rcFilterWalkableLowHeightSpans(rcContext* ctx, int walkableHeight, rcHeightfield& solid)
{rcAssert(ctx);rcScopedTimer timer(ctx, RC_TIMER_FILTER_WALKABLE);const int w = solid.width;const int h = solid.height;const int MAX_HEIGHT = 0xffff;//从上面没有足够空间让 agent 站在那里的 span 中移除可行走标志。for (int y = 0; y < h; ++y){for (int x = 0; x < w; ++x){for (rcSpan* s = solid.spans[x + y*w]; s; s = s->next){const int bot = (int)(s->smax);const int top = s->next ? (int)(s->next->smin) : MAX_HEIGHT;if ((top - bot) <= walkableHeight)s->area = RC_NULL_AREA;}}}
}

过滤有效区间和陡峭区间

同列相邻两区间之间距离的校验，保证最小可通过距离。可走变不可走，这种过滤器会首先查找当前span的所有“有效邻居区间”。需要注意的是：如果当前span已经不可走，则直接跳过了。

当前迭代区间为span1，遍历四个方向的轴邻居列，从下往上迭代轴邻居列的高度区间span2。
假设span1的上面还与其有同列相邻的span4，span2上面有与其同列相邻的span3。如果span3或span4不存在，则认为其高度为无穷大。
计算max(span1, span2)和min(span3, span4)的差值H，如果diff大于“配置可走高度walkableHeight”，则认为span2是一个“有效邻居区间”。可以证明，每一个轴邻居列上最多只会存在一个“有效邻居区间”。

可以很明显的看出，“有效邻居区间”限定了两种情况：

找到所有“有效邻居区间”后，过滤器会继续过滤“峭壁区间”。

如果有任意轴邻居列上没有任何“高度区间”，则认为当前span是”峭壁区间“。
如果有任意轴邻居列上没有”有效邻居区间“，则认为当前span是“峭壁区间”。
如果有任意轴邻居列上存在“有效邻居区间”span2，span2的上表面低于span的上表面，且span和span2的上表面高度差Diff大于配置参数“可爬坡高度”，则认为当前span是”峭壁区间”。
如果当前span本来可走，且判断为“峭壁区间”，则设置为“不可走”。

找不到峭壁区间后，还会进行一层间接峭壁区间的判断。

所有上表面高于span上表面的“有效邻居区间”中，上表面最高的“有效邻居区间”的上表面高度设为a。
所有上表面低于span上表面的“有效邻居区间”中，上表面最低的“有效邻居区间”的上表面高度设为b。
如果a减b大于配置参数“爬坡高度walkableClimb”，则认为当前span处于峭壁上--间接峭壁区间。
如果当前span本来可走，且判断为“间接峭壁区间”，则置为“不可走”。

void rcFilterLedgeSpans(rcContext* ctx, const int walkableHeight, const int walkableClimb,rcHeightfield& solid)
{rcAssert(ctx);rcScopedTimer timer(ctx, RC_TIMER_FILTER_BORDER);const int w = solid.width;const int h = solid.height;const int MAX_HEIGHT = 0xffff;// 标记边界Spanfor (int y = 0; y < h; ++y){for (int x = 0; x < w; ++x){for (rcSpan* s = solid.spans[x + y*w]; s; s = s->next){// 跳过不可走spanif (s->area == RC_NULL_AREA)continue;const int bot = (int)(s->smax);const int top = s->next ? (int)(s->next->smin) : MAX_HEIGHT;// 查找邻居的最小高度int minh = MAX_HEIGHT;// Min and max height of accessible neighbours.int asmin = s->smax;int asmax = s->smax;for (int dir = 0; dir < 4; ++dir){int dx = x + rcGetDirOffsetX(dir);int dy = y + rcGetDirOffsetY(dir);//跳过越界的邻居if (dx < 0 || dy < 0 || dx >= w || dy >= h){minh = rcMin(minh, -walkableClimb - bot);continue;}// From minus infinity to the first span.rcSpan* ns = solid.spans[dx + dy*w];int nbot = -walkableClimb;int ntop = ns ? (int)ns->smin : MAX_HEIGHT;//如果 spans 之间的间隙太小，则跳过 neightbourif (rcMin(top,ntop) - rcMax(bot,nbot) > walkableHeight)minh = rcMin(minh, nbot - bot);//其余的跨度for (ns = solid.spans[dx + dy*w]; ns; ns = ns->next){nbot = (int)ns->smax;ntop = ns->next ? (int)ns->next->smin : MAX_HEIGHT;// 如果Span之间的间隙太小，则跳过 neightbourif (rcMin(top,ntop) - rcMax(bot,nbot) > walkableHeight){minh = rcMin(minh, nbot - bot);// 查找最小/最大可访问邻居高度if (rcAbs(nbot - bot) <= walkableClimb){if (nbot < asmin) asmin = nbot;if (nbot > asmax) asmax = nbot;}}}}//如果下降到任何邻居Span小于 walkableClimb，将Span标记为RC_NULL_AREAif (minh < -walkableClimb){s->area = RC_NULL_AREA;}//如果所有邻居之间的差异太大，我们在陡坡上，将Span标记为RC_NULL_AREAelse if ((asmax - asmin) > walkableClimb){s->area = RC_NULL_AREA;}}}}
}

通过这三层过滤后就可以进行下一个步骤了。

划分可走表面为简单区域

我们在一个步骤中获取了具体可行走的表面，现在对于可行走表面我们需要一些步骤将可通过的区域分割成可以最终形成简单多边形的相邻的span（表面）区域。

创建开放高度场CompactHeightField

什么是开放高度场？和实体高度场有什么联系和区别？

无论是用实体高度场还是开放高度场，只是数据结构的不同，在逻辑上没有任何差别，Recast采用了开放高度场的数据结构进行体素化之后的所有算法。换句话说，再进行体素化构建实体高度场后，进行了一步实体高度场到开放高度场的转换。注意，开放高度场是在整个体素化过程结束之后才转换的，此时已经经过了高度区间的合并和过滤，换句话说，其实此时实体高度区间的下表面已经没有任何意义了。至于为什么选择开放高度场，更多的考虑可能是Recast关心的是场景中的“无实体障碍可通过空间”，而不关心“实体空间”。但是需要理解，本质上，使用哪一个高度场并没有什么区别。

因此，open span使用“地板（floor）”和“天花板（ceiling）”的术语。open span的地板是其关联的solid span的顶部。 open span的天花板是它所属的列中下一个更高的solid span的底部。如果没有更高的solid span，则open span的天花板是任意的最大值，例如整数的最大值。

CompactHeightField也叫紧缩高度场。我们不只关心实体空间，许多算法都是在solid span上方的空间上操作的。对于导航网格的生成来说，solid span的上表面是其最重要的部分，需要注意的是，开放高度场不是实体空间的简单反转。如果一个高度场列不包含任何solid span，则它也没有任何open span。最低的solid span以下的区域也被忽略，只有solid span上方的空间由open span来表示。

看起来有点眼花撩乱了可能，但其实说白了实体高度场就是可以拿来给角色踩的那一层，就是你现实生活中脚下的部分；开放高度场则是从你脚下的那一层到你头顶的那一层，也就是你人物本身可以移动的高度部分，如果你头顶没有东西那就是无限大——代表云，天空或者太阳。

开放高度场的创建相对简单，循环遍历所有实体span，如果span被标记为可通过，则确定它的最高值与其所在列中下一个更高span的最低值之间的开放空间。这些值分别形成了新的开放span的地板和天花板。如果一个实体span是它所在列中最高的span，则其关联的开放span将其天花板设置为任意高值（例如 Integer.MAX_VALUE）。新生成的开放span形成所谓的开放高度场：

bool rcBuildCompactHeightfield(rcContext* ctx, const int walkableHeight, const int walkableClimb,rcHeightfield& hf, rcCompactHeightfield& chf)
{const int w = hf.width;const int h = hf.height;const int spanCount = rcGetHeightFieldSpanCount(ctx, hf);//这里省略一些非核心代码......const int MAX_HEIGHT = 0xffff;// 填充rcCompactCell和rcCompactSpanint idx = 0;for (int y = 0; y < h; ++y){for (int x = 0; x < w; ++x){const rcSpan* s = hf.spans[x + y*w];// If there are no spans at this cell, just leave the data to index=0, count=0.if (!s) continue;rcCompactCell& c = chf.cells[x+y*w];c.index = idx;c.count = 0;while (s){if (s->area != RC_NULL_AREA){const int bot = (int)s->smax;const int top = s->next ? (int)s->next->smin : MAX_HEIGHT;chf.spans[idx].y = (unsigned short)rcClamp(bot, 0, 0xffff);chf.spans[idx].h = (unsigned char)rcClamp(top - bot, 0, 0xff);chf.areas[idx] = s->area;idx++;c.count++;}s = s->next;}}}return true;
}

创建邻居链接

我们现在有一个开放高度场，里面充满了不相关的开放span。下一步是找出哪些span形成了连续span的潜在表面。这是通过创建轴邻居链接（axis-neighbor links）来实现的。对于每个span，搜索其轴相邻列以查找候选对象。如果满足以下两个条件，则相邻列中的span被视为邻居span：

1. 两个span的顶部上升或下降的步长小于 walkableClimb的值。这允许将楼梯台阶和路缘这样的表面检测为有效的邻居。

这里又涉及到这个参数 walkableClimb了，这个参数的意义就是帮助我们正确的设置可行走高度差异的，一般来说，walkableClimb 应该大于 cellHeight 的两倍(walkableClimb > cellHeight * 2)。否则体素场的分辨率可能不够高，无法准确检测可通过的窗台（ledge）。窗台可以合并，有效地将它们的台阶高度加倍。对于楼梯来说，这尤其是个问题。（为什么楼梯这么难处理）

2. 当前span的地板和潜在邻居span的天花板之间的开放空间间隙足够大（大于walkableHeight）。

例如，如果agent要从一个span跨到另一个span，它会用头撞到邻居的天花板上吗？这是与潜在邻居之间的间隙检查。我们已经知道地板到天花板的高度对于每个单独的span来说都是足够的，该检查是在构建实体高度场时进行的。但是不能保证在潜在邻居之间移动时的间隙满足相同的高度要求。

bool rcBuildCompactHeightfield(rcContext* ctx, const int walkableHeight, const int walkableClimb,rcHeightfield& hf, rcCompactHeightfield& chf)
{//创建邻居链接const int MAX_LAYERS = RC_NOT_CONNECTED-1; //static const int RC_NOT_CONNECTED = 0x3f , 最多63层int tooHighNeighbour = 0;for (int y = 0; y < h; ++y){for (int x = 0; x < w; ++x){const rcCompactCell& c = chf.cells[x+y*w];for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i){rcCompactSpan& s = chf.spans[i];for (int dir = 0; dir < 4; ++dir){rcSetCon(s, dir, RC_NOT_CONNECTED); //先设置默认值RC_NOT_CONNECTED二进制是 111111const int nx = x + rcGetDirOffsetX(dir);const int ny = y + rcGetDirOffsetY(dir);// First check that the neighbour cell is in bounds.if (nx < 0 || ny < 0 || nx >= w || ny >= h)continue;// 检查当前span的所有邻居span，看这个span是否和当前span有邻居关系const rcCompactCell& nc = chf.cells[nx+ny*w];for (int k = (int)nc.index, nk = (int)(nc.index+nc.count); k < nk; ++k){const rcCompactSpan& ns = chf.spans[k];const int bot = rcMax(s.y, ns.y);const int top = rcMin(s.y+s.h, ns.y+ns.h);//检查2个span间的gap是否满足walkableHeight和walkableClimb的限制if ((top - bot) >= walkableHeight && rcAbs((int)ns.y - (int)s.y) <= walkableClimb){// Mark direction as walkable.const int lidx = k - (int)nc.index;if (lidx < 0 || lidx > MAX_LAYERS){tooHighNeighbour = rcMax(tooHighNeighbour, lidx);continue;}rcSetCon(s, dir, lidx);break;}}}}}}return true;
}

根据walkableRadius剔除边缘

我们现在获取了一系列连贯的开放高度场，但是还需要小小的优化一下：我们的人物模型本身也是有一定体积的，如果允许人物的模型中心移动到最边缘处可能会出现穿模的情况，所以具体的做法就是在所有的边缘处加上一层小小的剔除效果，即将障碍物周围可行走区域按radius值适当扩散不可行走区域。

此时的做法是对每一个“可走高度区间”加上一个“逻辑距离dist”的概念。该距离在逻辑上标识当前高度区间距离某个最近边界的距离。做两遍扫描，计算出每个span离边缘的距离,放到char*类型的dist 中。每次操作都是用小值替换大值，第一遍扫描从左上角往右下角，第二遍从右下角往左上角。这样就能保证每个位置的span计算出来的离边缘距离的准确性。然后再将离边距离小于两倍半径的span从可行走的span中剔除。

 从左下到右上遍历
for (int y = 0; y < h; ++y)
{for (int x = 0; x < w; ++x){const rcCompactCell& c = chf.cells[x+y*w];for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i){const rcCompactSpan& s = chf.spans[i];if (rcGetCon(s, 0) != RC_NOT_CONNECTED){// (-1,0)	左邻居const int ax = x + rcGetDirOffsetX(0);const int ay = y + rcGetDirOffsetY(0);const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 0);const rcCompactSpan& as = chf.spans[ai];// 轴邻居距离+2nd = (unsigned char)rcMin((int)dist[ai]+2, 255);if (nd < dist[i])dist[i] = nd;// (-1,-1) 左下邻居if (rcGetCon(as, 3) != RC_NOT_CONNECTED){const int aax = ax + rcGetDirOffsetX(3);const int aay = ay + rcGetDirOffsetY(3);const int aai = (int)chf.cells[aax+aay*w].index + rcGetCon(as, 3);// 斜方向的邻居距离+3nd = (unsigned char)rcMin((int)dist[aai]+3, 255);if (nd < dist[i])dist[i] = nd;}}if (rcGetCon(s, 3) != RC_NOT_CONNECTED){// (0,-1) 下邻居const int ax = x + rcGetDirOffsetX(3);const int ay = y + rcGetDirOffsetY(3);const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 3);const rcCompactSpan& as = chf.spans[ai];nd = (unsigned char)rcMin((int)dist[ai]+2, 255);if (nd < dist[i])dist[i] = nd;// (1,-1) 右下邻居if (rcGetCon(as, 2) != RC_NOT_CONNECTED){const int aax = ax + rcGetDirOffsetX(2);const int aay = ay + rcGetDirOffsetY(2);const int aai = (int)chf.cells[aax+aay*w].index + rcGetCon(as, 2);nd = (unsigned char)rcMin((int)dist[aai]+3, 255);if (nd < dist[i])dist[i] = nd;}}}}
}

根据ConvexVolume标记体素Area掩码

我们完成了开放高度场之后，还要考虑场景内的物体是否影响可行走问题，这涉及到了动态避障问题，我们在这里先介绍ConvexVolume——在Recast Navigation中，ConvexVolume（凸体体积）是一个用于动态标记导航网格特定区域的功能模块，主要用于定义自定义可行走区域、障碍物或特殊地形属性。

static const int MAX_CONVEXVOL_PTS = 12;
struct ConvexVolume
{float verts[MAX_CONVEXVOL_PTS*3];//Volume顶点数据float hmin;//Volume高度最低值float hmax;//Volume高度最高值int nverts;//Volume顶点数int area;  //区域类型,可自定义类型，比如Ground,Water,Grass等等
};

这是凸体体积的数据结构。

void rcMarkConvexPolyArea(rcContext* ctx, const float* verts, const int nverts,const float hmin, const float hmax, unsigned char areaId,rcCompactHeightfield& chf)
{// 遍历多边形范围内的体素for (int z = minz; z <= maxz; ++z){for (int x = minx; x <= maxx; ++x){const rcCompactCell& c = chf.cells[x+z*chf.width];for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i){rcCompactSpan& s = chf.spans[i];if (chf.areas[i] == RC_NULL_AREA)continue;if ((int)s.y >= miny && (int)s.y <= maxy){float p[3];p[0] = chf.bmin[0] + (x+0.5f)*chf.cs; p[1] = 0;p[2] = chf.bmin[2] + (z+0.5f)*chf.cs; if (pointInPoly(nverts, verts, p))  //判断点是否在poly范围内{chf.areas[i] = areaId; //设置体素area类型}}}}}
}

该函数是 Recast Navigation 中用于标记凸多边形区域内体素区域类型的关键函数，其作用是为导航网格生成预定义特殊区域（如水域、草地等）。其中：

Shape Height = Volume高度最高值hmax - Volume高度最低值hmin，Shape Descent = 坐标y最低值 - Volume高度最低值hmin，Shape Descent代表坐标面下沉值。

创建区域

到目前为止，所有的一切都是在为区域创建做准备。区域（region）是一组连续的span，表示可走表面的范围。它应该满足尽量大的、连续的、不重叠的、中间没有“洞”的“区域，区域的一个重要方面是，当投影到xz平面上时，它们会形成简单的多边形。Recast里提供了三种方式的区域切分方法：

分水岭算法（Watershed）

分水岭算法（watershed algorithm）用于初始区域的创建。使用分水岭类比，距离边界最远的span代表分水岭中的最低点，边界span代表可能的最高水位（和盆地的概念类似）。主循环从分水岭的最低点开始迭代，然后随着每个循环递增，直到达到允许的最高水位。这从最低点开始缓慢地“淹没”span。在循环的每次迭代期间，都会定位出低于当前水位的span，并尝试将它们添加到现有区域或创建新的区域。在区域扩展（region expansion）阶段，如果新淹没的span与一个已经存在的区域接壤，则通常会将其添加到该区域中。任何在区域扩展阶段，残留下来的新淹没的span都被用作创建新区域的种子。

分水岭算法通常用于图形处理领域，基于图像的灰度值来分割图像。这里唯一的不同点是用距离域来取代灰度值。距离域是指每个区间与可行走区域边缘的最近距离。距离域越大，等同于地势越低。

经典的Recast分区
创建最好的细分
通常最慢，一般用于离线处理，适合大地图
将Heightfield划分为没有孔或重叠的良好区域。
在某些极端情况下，此方法创建会产生孔洞和重叠
- 当小的障碍物靠近较大的开放区域时，可能会出现孔（三角剖分可以解决此问题）
- 如果您有狭窄的螺旋形走廊（即楼梯），则可能会发生重叠，这会使三角剖分失败
如果是预处理网格，通常是最佳选择，如果您有较大的开放区域，这种方法也适用。

这个算法的详细过程比较复杂，涉及到距离场的建立等内容，我这里感觉详细介绍太占篇幅，建议大家自己去查阅。

单调分区

单调算法，注重效率，在性能上是最快的
能将高度场划分为无洞和重叠的区域
创建长而细的多边形，有时会导致路径走弯
如果要快速生成导航网格，请使用此选项

按层分区

分层算法，折中思想，效果与性能都处于上述两种算法之间
将heighfield划分为非重叠区域
依靠三角剖分来处理孔（因此比单调分区要慢）
产生比单调分区更好的三角形
没有分水岭分区的特殊情况
速度可能很慢，并且会产生一些难看的镶嵌效果（仍然比单调效果更好），如果您的开放区域较大且障碍物较小（如果使用瓷砖则没有问题）
用于中小型瓷砖的导航网格的好选择

阶段总结

注意：Region 虽然是不重叠且没有洞的区域，但仍然有可能是凹多边形，无法保证 Region 内任意两点在二维平面一定可以直线到达。后续需要进行轮廓生成和凸多边形生成，为寻路做准备。

轮廓生成（Contour Generation）

在经过区域生成之后，region的描述是以span为颗粒度的，复杂度是否可以更简化一下？此时区域与区域之间的分界就是非常重要的信息了。其实我们只需要region的轮廓，而轮廓（Contour）就是描述区域边界的概念。

这个阶段生成表示源几何体的可行走表面的简单多边形（凸多边形和凹多边形）。轮廓仍然以体素空间为单位表示，但这是从体素空间（voxel space）回到向量空间（vector space）的过程中的第一步。

搜索区域边缘

从开放高度场结构转向轮廓结构时，最大的概念变化是从关注span的表面（surface）转变为关注span的边（edges）。

对于轮廓，我们关心span的边，有两种类型的边：

区域边（region ）：区域边是其邻居位于另一个区域中的span的边
内部边（internal）：内部边是其邻居在同一区域中的span的边

在此步骤中，我们希望将边分类为区域边或内部边。这些信息很容易找到。我们遍历所有span，对于每个span，我们检查所有轴邻居，如果轴邻居与当前span不在同一区域中，则该边将被标记为区域边。

// Mark boundaries.
for (int y = 0; y < h; ++y)
{for (int x = 0; x < w; ++x){const rcCompactCell& c = chf.cells[x+y*w];for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i){unsigned char res = 0;const rcCompactSpan& s = chf.spans[i];//如果span不存在region的ID,或者是边界，就不考虑这种spanif (!chf.spans[i].reg || (chf.spans[i].reg & RC_BORDER_REG)){flags[i] = 0;continue;}for (int dir = 0; dir < 4; ++dir){unsigned short r = 0;if (rcGetCon(s, dir) != RC_NOT_CONNECTED){const int ax = x + rcGetDirOffsetX(dir);const int ay = y + rcGetDirOffsetY(dir);const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);r = chf.spans[ai].reg;}//周围邻居所属的region和当前span的region相同，说明是连通的，标记为1if (r == chf.spans[i].reg)res |= (1 << dir);}//flags保存每个span四个方向是否为边界, 值是按位保存：1是边界（区域边），0不是边界（内部边）flags[i] = res ^ 0xf; //不连通的方向标记为1}}
}

查找区域轮廓

我们根据上一个步骤获取的区域边来绘制出区域的轮廓：

找到区域任意一个区域边A，以当前区域边开始算法。
如果当前是区域边，将当前区域边添加到轮廓中，然后顺时针旋转90度，继续判断旋转后的边。
如果当前是内部边，则进入到共当前边的邻居内，然后逆时针旋转90度，继续判断旋转后的边。
直到回到区域边A为止，结束，此时依次添加进轮廓中的所有边界边全部查找完毕。

看起来有点不知所云，用几张图展示一下这个过程：

找到了一条区域的边。

旋转了九十度之后找到了又一条区域边，加入轮廓。直到找到一条内部边后，我们根据此时箭头的方向步进到相邻的span中。

进入新的span中先逆时针旋转判断边，又是一个内部边，那就进去之后再逆时针旋转九十度，发现是区域边了，又顺时针旋转...不断循环往复直到我们回到起始span且面对起始方向。

遍历的过程我们还要不断地提取轮廓点，提取的规则如下：

体素左方是边界，轮廓点取其上方体素。
体素上方是边界，轮廓点取其右上方体素。
体素右方是边界，轮廓点取其右方体素。
体素下方是边界，轮廓点取其自身。

这样做的目的是，使得各个区域的轮廓线多边形的边互相重合，因为最终生成的navimesh数据多边形之间是共用一个边的，最终效果如下图所示：

从边到顶点

我们真正需要的内容不是边而是顶点，对于X-Z轴空间的点来说选取非常简单，取组成边的两个顶点即可：

确定顶点的y值就比较棘手了。这就是我们回归3D可视化的地方。在下面的例子中，我们选择哪个顶点?

选择最高的y值有两个原因：它确保最终顶点(x, y, z)位于源网格表面的上方。它还提供了一个通用的选择机制，以便所有使用该顶点的轮廓将使用相同的高度。

简化轮廓

我们已经为所有区域生成了轮廓。到这一步时，轮廓点由一系列连续的点组成的，在这些点里，有一些点是共线的，有一些点忽略后与最终轮廓形状差距不大。下面是一个宏观的视角。请注意，有两种类型的轮廓部分（contour sections）：

两个相邻区域之间门户（portal）的部分，即连接两个有效区域之间的边界边。
与“无效”区域接壤的部分。无效区域被称为“空区域”（null region），我在这里使用同样的术语。

秉持着没活硬整的态度，我们当然要继续优化。

即使在直线轮廓上，构成边的每个span都有一个顶点。显然，答案是否定的。唯一真正必需的顶点是那些在区域连接中发生变化的顶点。

去除一些对轮廓形状影响不大的点，得到更加丝滑的轮廓，可以有效减少锯齿轮廓。

这里约定一种顶点的概念：强制性顶点（Mandatory Vertices），它的含义是区域连接发生变化的顶点，可以看出有两种顶点：

连接有效区域的边界边上的顶点
连接有效区域和无效区域边界上的顶点

考虑一种特殊情况，可以很容易证明出，并不是所有的区域都有“强制性顶点”，此时如何进行上述算法呢？很简单，随便找两个相对较远的顶点作为强制性顶点即可。Recast的做法是，使用连接有效区域和无效区域边界上的顶点，从轮廓点中选择最左下和最右上的两个点作为初始简化点。

区域-区域门户（region-region portals）的简化很容易。我们丢弃除强制性顶点（mandatory vertices）之外的所有顶点：

// Add initial points.
bool hasConnections = false;
for (int i = 0; i < points.size(); i += 4)
{// point索引：0=x 1=y 2=z 3=r// 在之前的walkContour中产生，r的低16位如果是0，说明边界是不可行走的，否则该point有邻居regionif ((points[i+3] & RC_CONTOUR_REG_MASK) != 0){hasConnections = true;break;}
}// 如果轮廓有邻居region
if (hasConnections)
{for (int i = 0, ni = points.size()/4; i < ni; ++i){//下一个pointint ii = (i+1) % ni;//邻近的两个轮廓点接壤不同的regionconst bool differentRegs = (points[i*4+3] & RC_CONTOUR_REG_MASK) != (points[ii*4+3] & RC_CONTOUR_REG_MASK);//邻近的两个轮廓点里，一个接壤其他region，另一个接壤不可行走const bool areaBorders = (points[i*4+3] & RC_AREA_BORDER) != (points[ii*4+3] & RC_AREA_BORDER);// 总之邻近的两个轮廓点接壤不是同一个region，则记录这个点if (differentRegs || areaBorders){simplified.push(points[i*4+0]);simplified.push(points[i*4+1]);simplified.push(points[i*4+2]);simplified.push(i);}}
}

帮助我们找到初始的简化点。

// 如果不连接任何region则没有simplified点，那么选择左下和右上的两个点作为simplified点
if (simplified.size() == 0)
{int llx = points[0];int lly = points[1];int llz = points[2];int lli = 0;int urx = points[0];int ury = points[1];int urz = points[2];int uri = 0;for (int i = 0; i < points.size(); i += 4){int x = points[i+0];int y = points[i+1];int z = points[i+2];if (x < llx || (x == llx && z < llz)){llx = x;lly = y;llz = z;lli = i/4;}if (x > urx || (x == urx && z > urz)){urx = x;ury = y;urz = z;uri = i/4;}}simplified.push(llx);simplified.push(lly);simplified.push(llz);simplified.push(lli);simplified.push(urx);simplified.push(ury);simplified.push(urz);simplified.push(uri);
}

根据maxSimplificationError参数来决定丢弃哪些顶点以得到简化的线段——代表网格的边可以偏离源几何体的最大距离，较低的值将导致网格边缘更准确地遵循 xz 平面的几何轮廓，但会增加三角形数量。
不建议将值设为0，因为它会导致最终网格中的多边形数量大幅增加，处理成本很高。

现在从强制顶点（mandatory vertices）开始，将最远顶点添加回来，这样原始顶点与简化边之间的距离都不会超过maxSimplificationError。

下面的图中展示这一过程：

首先找到左下和右上两个点

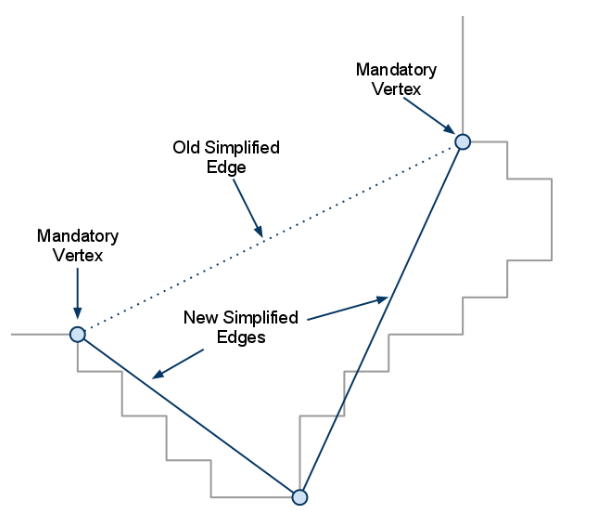
如果简化后的边长度超过了maxSimplificationError我们把离简化边最远的点加回来。

重复这个过程，直到不再有顶点到简化边的距离超过允许值：

长边轮廓二分为短边

区域-区域之间的轮廓已经简化完成了，而针对区域-空区域之间的轮廓简化还有别的做法：使用maxEdgeLen参数重新插入顶点，以确保没有线段超过最大长度，它是通过检测长边，然后将它们分成两半来实现这一点的。它会继续这个过程，直到检测不到过长的边为止。

// Split too long edges.
if (maxEdgeLen > 0 && (buildFlags & (RC_CONTOUR_TESS_WALL_EDGES|RC_CONTOUR_TESS_AREA_EDGES)) != 0)
{for (int i = 0; i < simplified.size()/4; ){const int ii = (i+1) % (simplified.size()/4);const int ax = simplified[i*4+0];const int az = simplified[i*4+2];const int ai = simplified[i*4+3];const int bx = simplified[ii*4+0];const int bz = simplified[ii*4+2];const int bi = simplified[ii*4+3];// Find maximum deviation from the segment.int maxi = -1;int ci = (ai+1) % pn;// Tessellate only outer edges or edges between areas.bool tess = false;// Wall edges. 不可行走边界if ((buildFlags & RC_CONTOUR_TESS_WALL_EDGES) && (points[ci*4+3] & RC_CONTOUR_REG_MASK) == 0)tess = true;// Edges between areas. region边界if ((buildFlags & RC_CONTOUR_TESS_AREA_EDGES) && (points[ci*4+3] & RC_AREA_BORDER))tess = true;if (tess){int dx = bx - ax;int dz = bz - az;if (dx*dx + dz*dz > maxEdgeLen*maxEdgeLen)  //线段超过最大长度maxEdgeLen，就分为两个线段{// Round based on the segments in lexilogical order so that the// max tesselation is consistent regardles in which direction// segments are traversed.const int n = bi < ai ? (bi+pn - ai) : (bi - ai);// ai与bi相差n个索引if (n > 1) // n > 1，说明ai bi之间有轮廓点，可切分{if (bx > ax || (bx == ax && bz > az))maxi = (ai + n/2) % pn;elsemaxi = (ai + (n+1)/2) % pn;}}}// If the max deviation is larger than accepted error,// add new point, else continue to next segment.if (maxi != -1)  // maxi位置的点插入到simplified中{// Add space for the new point.simplified.resize(simplified.size()+4);const int n = simplified.size()/4;for (int j = n-1; j > i; --j){simplified[j*4+0] = simplified[(j-1)*4+0];simplified[j*4+1] = simplified[(j-1)*4+1];simplified[j*4+2] = simplified[(j-1)*4+2];simplified[j*4+3] = simplified[(j-1)*4+3];}// Add the point.simplified[(i+1)*4+0] = points[maxi*4+0];simplified[(i+1)*4+1] = points[maxi*4+1];simplified[(i+1)*4+2] = points[maxi*4+2];simplified[(i+1)*4+3] = maxi;}else{++i;}}
}

检查和合并空洞

首先我们要检查空洞（为什么还要考虑空洞问题呢？在Recast Navigation中，轮廓生成后仍需检查空洞，根本原因在于区域划分阶段无法完全消除所有空洞风险，且轮廓生成过程可能引入新的空洞问题）。

首先我们要知道一个关于三角形叉乘和面积的关系：如果是顺时针方向，求取的面积值是负的，如果是逆时针方向，求取的面积值是正的。

而正常轮廓线的顶点是顺时针存储，空洞轮廓线的顶点是逆时针存储（在查找轮廓中完成）：

所以根据叉乘算出每个轮廓多边形的有向面积，如果结果为小于0，则为轮廓点的顺序为逆时针，这个轮廓就是一个空洞。

int nholes = 0;
for (int i = 0; i < cset.nconts; ++i)
{rcContour& cont = cset.conts[i];// If the contour is wound backwards, it is a hole.winding[i] = calcAreaOfPolygon2D(cont.verts, cont.nverts) < 0 ? -1 : 1;if (winding[i] < 0)nholes++;
}

现在我们找到空洞之后，就要去合并空洞：

找到空洞的左下方顶点B4
将轮廓线所有顶点与B4相连，如果连线与轮廓线、空洞都不相交，则连线构成1条对角线。上图满足条件的有A5B4，A5B4，A4B4
选择其中长度最短的1条对角线A5B4，将空洞合并到轮廓线中

最终轮廓线的顶点序列为A5、A6、A1、A2、A3、A4、A5、B4、B1、B2、B3、B4。(如果包含多个空洞的话，将空洞按左下方顶点排序，依次迭代将外围轮廓与空洞进行合并。)

阶段总结

在这个阶段结束时，我们有形成简化多边形的轮廓。顶点仍然在体素空间中，但是我们正在回到向量空间的路上。

凸多边形生成（Convex Polygon Generation）

有了轮廓的数据之后，就有了一片区域的边，那么此时就需要对区域进行更加详细的定位，例如寻路是要具体寻到某一个点，并且区域内部任意两点并不是一定直线联通的，所以要将区域划分成更加细化的可以描述整个区域面的信息的数据。此时采用的是将区域划分成一些凸多边形的集合，这些凸多边形的并集就是整个区域。本阶段是从由轮廓表示的简单多边形生成凸多边形。这也是我们从体素空间回到向量空间的地方。

本阶段的主要任务如下：

轮廓的顶点在体素空间中，这意味着它们的坐标采用整数格式并表示到高度场原点的距离。因此轮廓顶点数据被转换为原始源几何体的向量空间坐标。
每个轮廓完全独立于所有其他轮廓。在此阶段，我们合并重复的数据并将所有内容合并到一个单一网格中。
轮廓只能保证表示简单的多边形，包括凸多边形和凹多边形。凹多边形对导航网格来说是没有用的（凸多边形中，任意两点间的直线路径必然完全位于多边形内部，确保AI移动时不会穿越障碍物。而凹多边形存在“凹陷”区域（内角>180°），两点间的直线可能穿出多边形边界，进入未知区域（如墙体或悬崖），导致路径失效或角色卡死），所以我们根据需要细分轮廓以获得凸多边形。
我们收集指示每个多边形的哪些边连接到另一个多边形的连接信息（多边形邻居信息）。

坐标转换和顶点数据合并是相对简单的过程，所以我不会在这里讨论它们。如果您对这些算法感兴趣，可以查看文档详尽的源代码。这里我们将专注于凸多边形的细分。对每个轮廓会执行以下步骤：

对每个轮廓进行三角面化（triangulate）。
合并三角形以形成最大可能的凸多边形。

我们通过生成邻居连接信息来结束这个阶段。

三角形剖分（Triangulation）

针对凹多边形的三角划分：耳裁法（为什么这里又是针对凹多边形呢？其实这个方法也适用于凸多边形而且更简单）

每次迭代凹多边形，将其分成两部分，一个三角形和剩余的部分。然后迭代“剩余的部分”，继续划分，直到没有三角形可以划分位置。
算法的核心点是如何对每次的“剩余多边形”划分出一个三角形。
采用的方法很简单，基于“任意不共线三点构成三角形”的理论，每次寻找多边形相邻的两条边，如果其不共直线，那么连接这两条边的三个端点，就可以形成一个三角形。
但是需要注意的是，这样形成的三角形可能会是多边形外部的，注意区分剔除即可。

从所有潜在的候选者中，选择具有最短的新边的那个。新边被称为“分割边”（partition edges），或简称为“分割”（partition）。该过程继续处理剩余的顶点，直到三角形剖分完成。

为了提高性能，三角形剖分在轮廓的 xz 平面投影上运行。

首先我们要构建可能的切割边：
三角形剖分是通过沿着轮廓的边往前走（walking the edges of the contour）来完成的，以任意端点开始，沿着一个方向依次去找两个边，如果两个边不共线，则连接两边不重合的点，形成一条连线，称为“分割边”。对每一个点进行该过程，会形成很多分割边，剔除那些在多边形外部的分割边，剩余的就是有效分割边。

在上述所有有效分割边中，找出一条最短的分割边，然后将该分割边与“形成该分割边的其他两条多边形边”形成一个三角形。此时就将凹多边形划分出了一个三角形。剩余多边形继续重新划分“分割边”(每进行一次分割就要重新分割)，重复该过程即可。

使用最短分割边的原因是，在概率上试图每次分出去一个尽可能小的三角形，以此增加最终分割的三角形的数量，进而增强分割后的信息量。

合并为凸多边形（凸多边形化）

合并只能发生在从单个轮廓创建的多边形之间。不会尝试合并来自相邻轮廓的多边形。

请注意，我已切换到一般形式的“多边形”（polygon）而不是三角形（triangle）。虽然初始合并将在三角形之间进行，但随着合并过程的进行，非三角形多边形可能会相互合并。

该过程如下：

找出所有可以合并的多边形。
从该列表中，选择共享边最长的两个多边形并将它们合并。
重复这个过程直到没有可以进行的合并。

如果满足以下所有条件，则可以合并两个多边形：

多边形共享一条边。
合并后的多边形仍然是凸多边形。
合并后的多边形的边数不会超过maxVertsPerPoly

为什么是最长边：这是一种“伪贪心”思想，试图从概率上使每次合并的多边形更大，从而减少合并后多边形的数量，数量越少，后续的Detour算法越简单。

如何确定合并后的多边形是否为凸多边形：此检查的关键就是保证合并后的多边形所有内角不超过180度。

合并多边形ABC和多边形ADC，两者的公共边是AC，前提条件是，∠ABC和∠ADC都是小于180度的。问题是证明合并后的∠BAD和∠BCD在什么情况下会小于180度，在什么情况下会大于180度。

采用的方式是，连接BD作为参考线。BD产生的条件，从公共边两端点中选择一点A，点A在两个多边形中分别有两条边，选择不是公共边的那一条，即图中的AB和AD作为“校验边”，此时连接两条校验边的另外一个端点B和D，形成参考线。

形成参考线后，只需要保证公共边两端点分属在参考线的两侧，即证明以刚才选择点A所形成的内角∠BAD是一个小于180度的角。

然后再以公共边另外一个端点C重复上述过程，证明∠BCD是否满足条件。

其实很好理解，用公共边一个端点和参考线一定可以形成一个三角形，只需要判断这个三角形的当前内角是合并多边形的内角还是外角就可以了。而当公共边的两端点在参考线两侧的时候，恰好对应的是内角。至于以公共边的两端点来进行这个校验，是因为我们保证了，合并之前的多边形都是凸多边形，意味着所有不参与合并的角本来就是满足条件的，不需要检查了，而参与合并的角，就是公共边两端点的角。

一定要理解：上述算法的所有思路，都是建立在合并之前的两个多边形都是凸多边形的基础上。

// Merge polygons.
if (nvp > 3)
{for(;;){// Find best polygons to merge.int bestMergeVal = 0; //共边的长度值int bestPa = 0, bestPb = 0, bestEa = 0, bestEb = 0;for (int j = 0; j < npolys-1; ++j){         unsigned short* pj = &polys[j*nvp];for (int k = j+1; k < npolys; ++k){unsigned short* pk = &polys[k*nvp];int ea, eb;// 返回可合并的边的长度int v = getPolyMergeValue(pj, pk, mesh.verts, ea, eb, nvp);// 找到最长的边进行合并if (v > bestMergeVal){bestMergeVal = v;bestPa = j;bestPb = k;bestEa = ea;bestEb = eb;}}}if (bestMergeVal > 0){// Found best, merge.unsigned short* pa = &polys[bestPa*nvp];unsigned short* pb = &polys[bestPb*nvp];//pa和pb合并成一个，最后放到pa里mergePolyVerts(pa, pb, bestEa, bestEb, tmpPoly, nvp);//最后的poly放到pbunsigned short* lastPoly = &polys[(npolys-1)*nvp];if (pb != lastPoly)memcpy(pb, lastPoly, sizeof(unsigned short)*nvp);npolys--;}else{// Could not merge any polygons, stop.break;}}
}

构建边的邻接关系

虽然有了凸多边形信息，但是每个凸多边形的邻接关系是不知道的，因此这一步的目的就是要遍历整个网格中的所有多边形并生成邻接信息（connection information），方便后续寻路使用。

struct rcEdge
{unsigned short vert[2];     // 边的两个点unsigned short polyEdge[2]; // 邻接的两个多边形的边的索引unsigned short poly[2];     // 邻接的两个多边形的索引
};

这是邻接边的数据结构。

遍历多边形，初始化边信息rcEdge，每条边两个顶点的索引v0、索引v1，保证v0<v1
再进行一次遍历，这次筛选出顶点索引v0 > 顶点索引v1形成的边，如果两个顶点与某个rcEdge相同，则补全rcEdge的邻接信息
最后把rcEdge信息保存到mesh.polys中，每个poly用长度为2*maxVertsPerPoly的short表示，[0, maxVertsPerPoly)表示多边形的顶点索引，[maxVertsPerPoly, 2*maxVertsPerPoly)表示顶点邻接的多边形索引

阶段总结

许多算法只能用于凸多边形。因此，这一步将构成轮廓的简单多边形细分为凸多边形网格。这是通过使用一个适用于简单多边形的三角形划分（triangulation），然后再将三角形合并为最大可能的凸多边形来实现的。

详细网格生成（Detailed Mesh Generation）

构建导航网格的第五个也是最后一个阶段，即生成具有详细高度信息的三角形网格。

为什么要执行这一步？

在三维空间中，多边形网格可能无法充分遵循源网格的高度轮廓，无论拆分单元的粒度有多小，都不可能完全拟合原实物空间，总是存在误差。而经过多步针对“体素块”的操作后，这些误差可能被放大，导致了Mesh导航面其实只是“原场景”的一个“大概表面”。比如楼梯。此时就需要，在Mesh多边形的基础上，去对比“原场景表面”，然后对Mesh多边形进行再加工——添加高度细节，使其最大限度的贴合原场景表面，减少误差。

该阶段的主要步骤如下，对于每个多边形：

对多边形的外壳边缘（hull edges）进行采样。向任何偏离高度补丁数据超过detailSampleMaxError的边添加顶点。
对多边形执行Delaunay 三角形剖分。
对多边形的内部表面进行采样。如果表面与高度补丁数据的偏差超过 detailSampleMaxError的值，则添加顶点。更新新顶点的三角形剖分。

这个阶段增加了高度细节，这样细节网格（detail mesh）将在所有轴上与源网格的表面相匹配。为了实现这一点，我们遍历所有多边形，并在多边形与源网格过度偏离时沿着多边形的边和其表面插入顶点。

从技术上来讲，从寻路的角度来看，这一步不是必需的。凸多边形网格是生成适合使用寻路算法的图所需要的全部，而在上一阶段创建的多边形网格提供了所有必要的数据。这尤其适用于使用物理或ray-casting将agent放置在源网格表面的情况。事实上，Recast Navigation的Detour库只使用多边形网格来寻路。这个阶段生成的高度细节被认为是可选的，当包含它时，它仅用于完善由各种Detour函数返回的点的位置。

同样重要的是要注意，这个过程仍然只会产生原始网格表面的一个更好的近似。体素化过程已经决定了精确的位置是不可能的。除此之外，由于搜索性能和内存的考虑，过多的高度细节通常比太少的细节更糟糕。

因为CSDN现在又非常卡了，加上这部分内容并不是必须的，容我偷个懒就不介绍这部分的内容了，大家有兴趣的可以去看知乎原文：(99+ 封私信 / 80 条消息) Recast Navigation源码分析：导航网格Navmesh的生成原理 - 知乎 (zhihu.com)

这篇文章里还提到了关于NavMesh里的一些缺点：

（1）RecastNavigation所有操作都基于地表面，因此，对空中的对象的交互，用它是无法完成的。现在国产武侠类 MMORPG 里大行其道的轻功、甚至御剑飞行，是无法只单纯依赖 RecastNavigation 的数据去实现的。特别是对于某些具有层次错落结构的地形，就非常容易出现掉到两片导航网格的夹缝里的情况。这类机制的实现需要其他场景数据的支持，通常这时会结合其他引擎，如physx

（2）像《塞尔达传说：旷野之息》的爬山、《忍者龙剑传》的踩墙这种机制，则会在生成导航网格的阶段就会遇到麻烦。因为设计前提2的存在，RecastNavigation 是无法对与地面夹角小于或等于90°的墙面生成导航网格的。因此需要从另外的机制、设计上去规避或处理。不过，Unity 2017 已经可以支持了在各种角度的墙面生成导航网格了：Ceiling and Wall Navigation in Unity3D

当然，这篇文章成文时间是22年，很有可能他说的这些内容都已经实现了。我去翻了下原作者的其他文章，他显然食言了呀，没有做Recast Navigation后续的内容了，只有关于构建导航网络的解析，我后续会继续研究NavMesh的内容的，就放在后续来讲解吧。