---

题目链接：

662. 二叉树最大宽度

---

题目描述：

---

解法

这里的宽度指的是一层的最右边的非空节点到一层的最左边的非空节点，一共的节点数。

解法一：硬来（会超时，因为可能会有3000个数的左右各1500个节点的最恶心的情况）

仿照之前的层序遍历，把空节点也加进去。（要注意，遇到空节点要添加两个空孩子）

解法二：利用数组存储二叉树的方式，给节点编号。

宽度就是这个队列的队尾和队头相减再加一。

也可以直接搞一个数组来模拟。

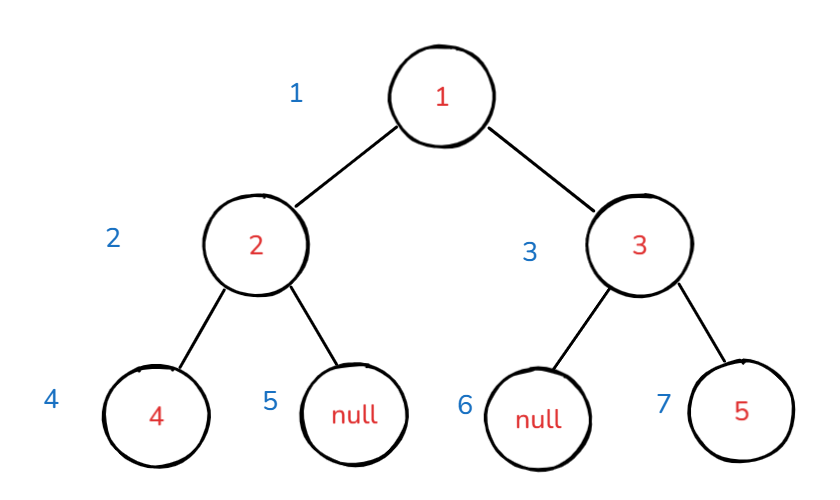
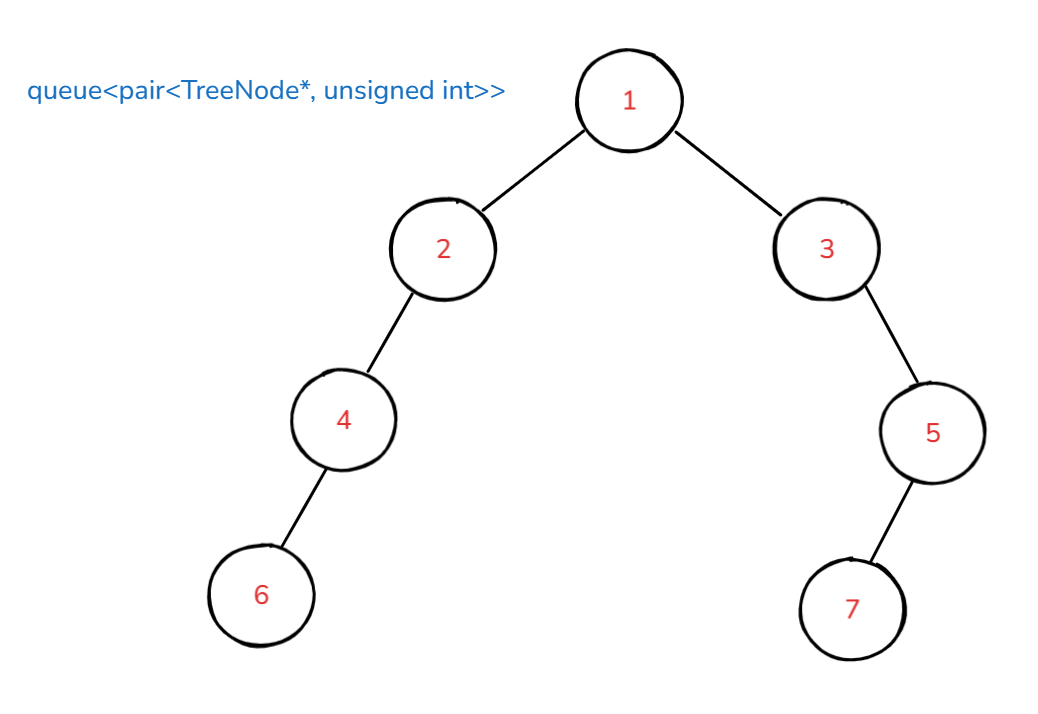
注意细节：下标有可能会溢出。

不过当我们相减之后，即使溢出，结果也是正确的。因为存储实际上是一个环，所以我们可以使用无符号整数来存储。

---

C++ 算法代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;              // 节点值*     TreeNode *left;       // 左子节点指针*     TreeNode *right;      // 右子节点指针*     TreeNode() : val(0), left(nullptr), right(nullptr) {}             // 默认构造函数*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}        // 带值的构造函数*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}  // 完整构造函数* };*/
class Solution 
{
public:int widthOfBinaryTree(TreeNode* root) {// 计算二叉树最大宽度算法// 基本思路：使用层序遍历，同时为每个节点分配位置编号// 宽度定义为：每一层最右边节点与最左边节点的位置差+1// 使用数组模拟队列，存储节点和其位置编号// 使用unsigned int避免大数时可能的整数溢出vector<pair<TreeNode*, unsigned int>> q;q.push_back({root, 1});  // 根节点入队，位置编号为1unsigned int ret = 0;    // 存储最大宽度结果while(q.size())  // 只要队列不为空，就继续处理{// 计算当前层的宽度：最右节点位置减去最左节点位置再加1auto& [x1, y1] = q[0];       // 当前层最左边的节点x1及其位置y1auto& [x2, y2] = q.back();   // 当前层最右边的节点x2及其位置y2ret = max(ret, y2 - y1 + 1); // 更新最大宽度// 准备处理下一层节点vector<pair<TreeNode*, unsigned int>> tmp; // 临时数组，存储下一层的节点// 遍历当前层的所有节点，将其子节点加入到下一层for(auto& [x, y] : q){// 关键：为子节点分配位置编号// 左子节点的位置是父节点位置的2倍if(x->left) tmp.push_back({x->left, y * 2});// 右子节点的位置是父节点位置的2倍加1if(x->right) tmp.push_back({x->right, y * 2 + 1});}q = tmp;  // 更新队列，准备处理下一层}return ret;  // 返回最大宽度}
};