目录
什么是下三角矩阵？
我们要存哪些元素？一共几个？
推导索引映射公式
核心问题：给定 (i,j)，如何计算 k？
什么是下三角矩阵？
一个 n × n 的矩阵，如果它在主对角线以上的所有元素都是 0，那么它就是一个下三角矩阵。
比如 4×4 的矩阵：
[ a00 0 0 0 ]
[ a10 a11 0 0 ]
[ a20 a21 a22 0 ]
[ a30 a31 a32 a33 ]
我们发现：
-
只有 行号 ≥ 列号（即 i ≥ j）的位置有非零元素。
-
其他地方（即 i < j）全是 0，不需要存！
一个矩阵 A 是一个二维的数字表格。对于一个 n×n 的矩阵来说：
-
它一共有 n 行，每行 n 个元素。
-
每个元素用两个下标表示：
A[i][j]，其中 i 是行号，j 是列号。
在 C 或 C++ 中我们常写成：A[i][j]
我们要存哪些元素？一共几个？
我们只存矩阵下三角区域的元素（含对角线），也就是：
-
第1行：只存1个元素（A₁₁）
-
第2行：存2个元素（A₂₁，A₂₂）
-
第3行：存3个元素（A₃₁，A₃₂，A₃₃）
-
...
-
第n行：存n个元素（Aₙ₁，...，Aₙₙ）
所以总共要存的元素个数是：1 + 2 + 3 + ... + n = n * (n + 1) / 2 个元素
推导索引映射公式
假设我们用一维数组 a[k] 来存下三角矩阵的非零值，用行主顺序（row-major order）存储。
设矩阵是 n × n，下标从 1开始，那么我们就要构造一个下标转换公式：
你给我 i, j（i ≥ j），我要算出它在数组 a[] 里的位置
我们按行来存：先存第1行，再第2行，再第3行……
例子（n=4）中，存储顺序是：
a[0] = A[1][1]
a[1] = A[2][1]
a[2] = A[2][2]
a[3] = A[3][1]
a[4] = A[3][2]
a[5] = A[3][3]
...
核心问题：给定 (i,j)，如何计算 k？
我们想要的 k 是：
第1行：有 1 个元素（j 从 1 到 1）
第2行：有 2 个元素（j 从 1 到 2）
...
第(i-1)行：有 (i - 1) 个元素
=> 总共 (1 + 2 + ... + (i-1)) = (i-1) * i / 2 个元素
加上当前这一行中第 j 个元素（从左往右第 j 个）
所以： k = 前 (i - 1) 行的元素个数 + 第 j 列在当前行中的偏移量(j - 1)
✅ 最终公式：k = (i - 1) * i / 2 + (j - 1)
注意：这里的 k 是数组 a[k] 中的下标（从0开始）
⚠️ 重要说明
-
这个公式只适用于 i ≥ j（也就是下三角部分）
-
如果你输入了 i < j，就说明这个元素是 0，不在数组中！
列主顺序存储：（这里不再详细说明）
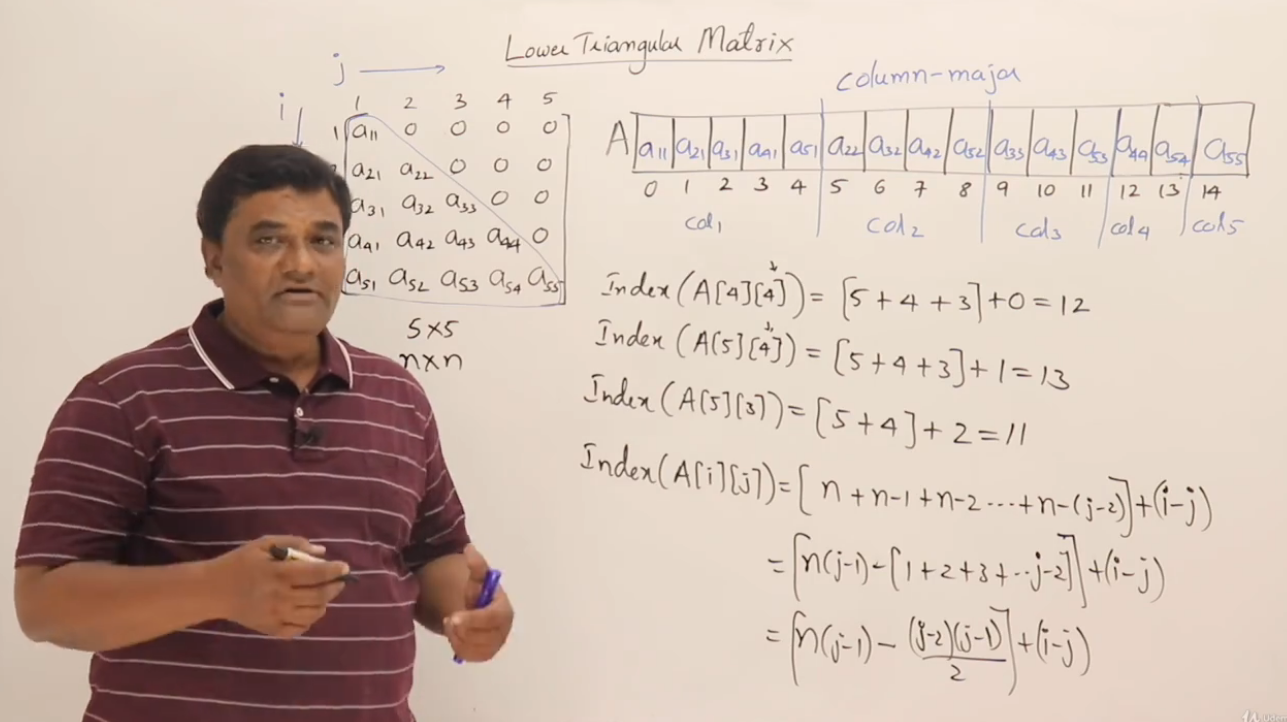示例验证
矩阵如下（n=4）：
1 0 0 0
2 3 0 0
4 5 6 0
7 8 9 10
我们来看 A[4][2] 是多少：
-
i = 4, j = 2
-
index = (4 - 1) * 4 / 2 + (2 - 1) = 3 * 4 / 2 + 1 = 6 + 1 = 7
-
a[7] = A[4][2] = 8
