前言

依旧是只会写签到题的一场。

---

A.约数个数和

题目传送门：约数个数和

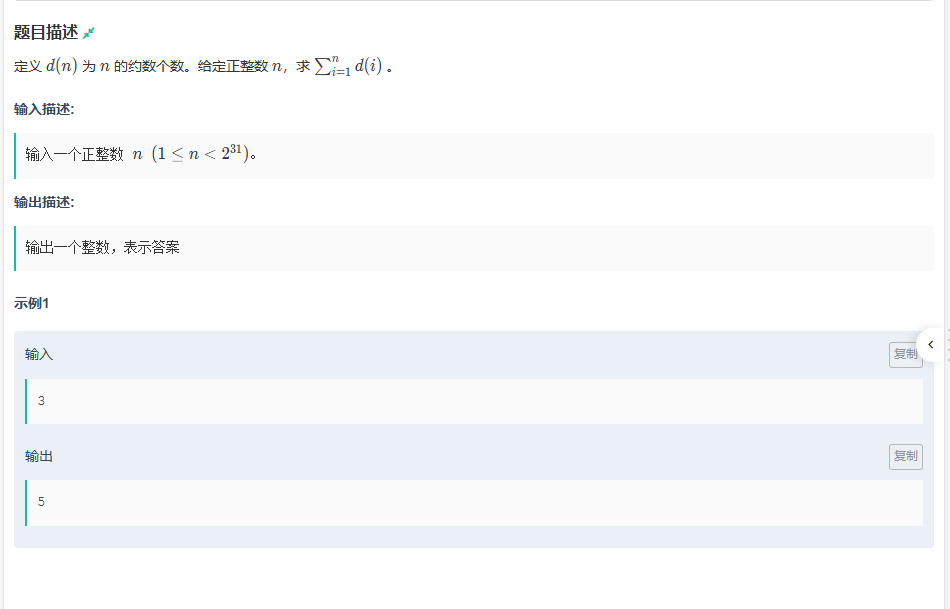
这一题利用到了整除分块，如果不这样的话，数据太大，会时间超限。
AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll ans=0;
void solve()
{ll n;cin>>n;for(ll l=1,r;l<=n;l=r+1){r=n/(n/l);ans+=(n/l)*(r-l+1);}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

整除分块(相当于约数求和)

介绍：整除分块（也叫数论分块）是数论和算法竞赛中常用的优化技巧，主要用于高效计算形如
$$\sum _{i=1}^{n}f(i)\cdot g\left(\lfloor \frac{n}{i}\rfloor \right)$$ 的求和式，核心思想是利用「整除的周期性」，将求和式中结果相同的区间合并，减少计算次数。
一、整除分块的核心原理：
利用整除的「周期性」对于固定的 n，当 i 从 1 到 n 变化时，$$\lfloor \frac{n}{i}\rfloor$$ 的值会分段相同。
例如：(n=10) 时，$$\lfloor \frac{10}{i}\rfloor$$ 的取值如下：

可以看到，$$\lfloor \frac{n}{i}\rfloor$$ 的值会形成连续的区间段（如 i=4,5 时，值都是 2；$$i=6\sim 10$$时，值都是 1）。关键发现：
对于某个值 $$k=\lfloor \frac{n}{i}\rfloor$$，所有能使 $$\lfloor \frac{n}{i}\rfloor =k$$的 i 会构成一个连续区间 ([l, r])，其中：左端点 l 是当前区间的起始右端点 r 满足：
$$r=\lfloor \frac{n}{k}\rfloor =\lfloor \frac{n}{\lfloor \frac{n}{l}\rfloor }\rfloor$$
利用这一性质，我们可以将原本需要遍历 n 次的求和，优化为遍历所有不同的 k 对应的区间段，$$时间复杂度从O(n)降到O(\sqrt{n})（因为不同的k最多有2\sqrt{n}个）$$。
模板：

long long sum = 0;
for (int l = 1, r; l <= n; l = r + 1) {int k = n / l;r = n / k;  // 计算当前段的右端点sum += (r - l + 1) * k;
}

相关例题：取模

题目传送门：取模



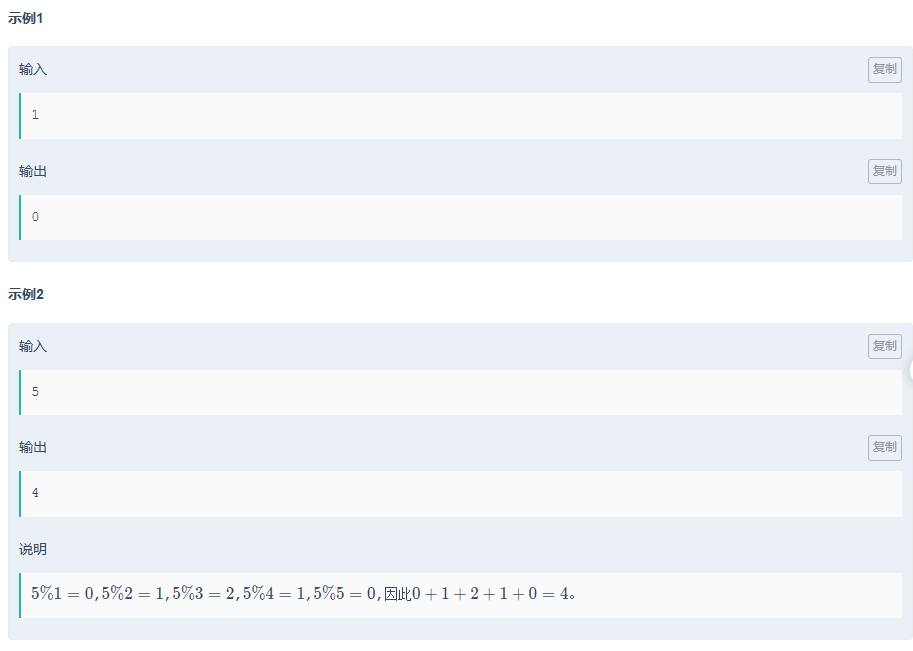
对于这一题，同样可以通过一系列推理，将其转换到整除分块
利用取模的数学定义：
$$n\%i=n-i\cdot \lfloor \frac{n}{i}\rfloor$$因此，原求和式可展开为：
$$\sum _{i=1}^n\left(n\%i\right)=\sum _{i=1}^n\left(n-i\cdot \lfloor \frac{n}{i}\rfloor \right)$$拆分求和式：
$$\sum _{i=1}^n\left(n\%i\right)=\sum _{i=1}^{n}n-\sum _{i=1}^n\left(i\cdot \lfloor \frac{n}{i}\rfloor \right)$$
对于i求和，可以通过等差数列求和推理出来
AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll mod=998244353;
void solve()
{ll n;cin>>n;__int128 ans=0;//特别注意类型，因为数据范围非常大for(__int128 l=1,r;l<=n;l=r+1){ll k=n/l;r=n/k;ans+=k*((r-l+1)*(r-l)/2+(r-l+1)*l)%mod;}ll an=((__int128)n*(__int128)n-ans)%mod;cout<<an<<endl;
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

B.异或期望的秘密

题目传送门：异或期望的秘密

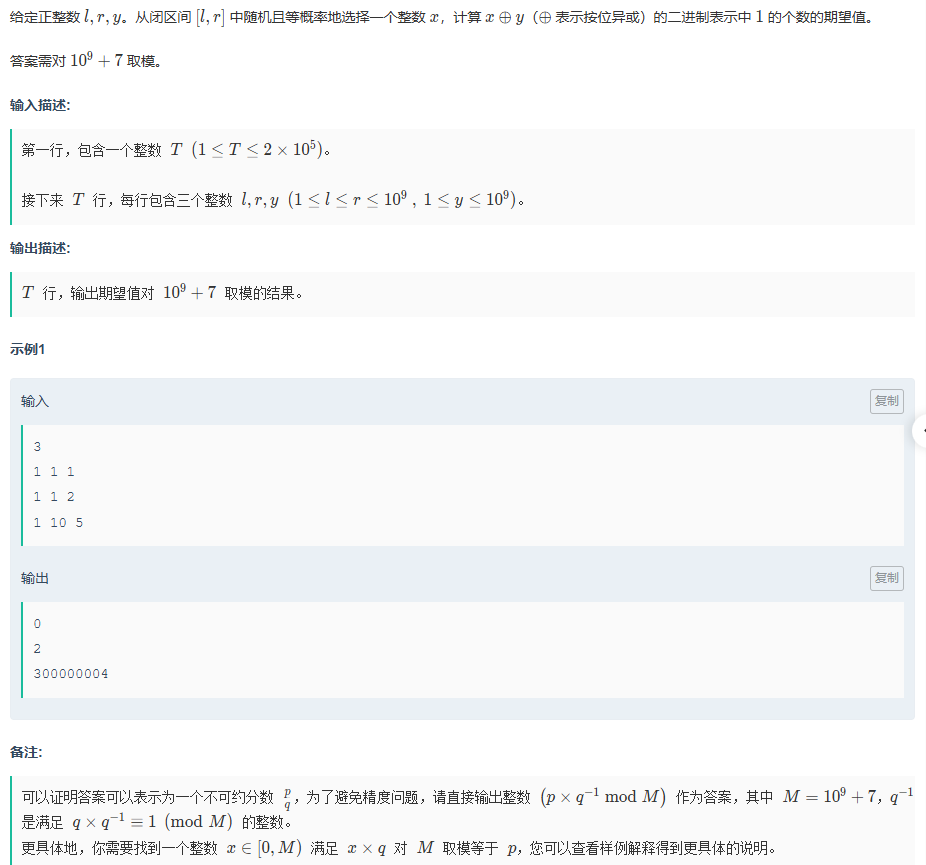
这一题用到的知识就很多了，有关于二进制的规律，以及乘法逆元，还有数学期望的计算；
思路：
通过数据范围可以发现，直接进行循环肯定会时间超限，为此就有了一个很妙的方法，利用到异或以及二进制的规律，通过遍历y在bitset的每一位，通过当前y在二进制下的0与1，与L到R之间相同位数下的1的个数来进行判断，由于异或的性质，相同为0，由此来反着推出贡献为1的总数，最后再通过乘法逆元。
AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll mod=1e9+7;
ll qmod(ll x,ll y)//乘法逆元（快速幂）
{ll sum=1;while(y){if(y&1){sum*=x;sum%=mod;}x*=x;x%=mod;y>>=1;}return sum;
}
ll f(ll x,ll i)//计算x第i位的1的个数
{if(x==0)return 0;ll sum=0;ll val=1ll<<i;//每个周期的贡献值ll curr=1ll<<(i+1);//一个周期的大小ll re=x%curr-val+1;//计算不足一个周期的贡献值sum+=val*(x/curr);//计算整周期的贡献sum+= max((ll)0,re);//比较剩余周期是否有贡献值sum%=mod;return sum;
}
void solve()
{ll l,r,y;cin>>l>>r>>y;ll k=r-l+1;ll ans=0;bitset<31>m(y);//方便进行异或for(ll i=0;i<=29;i++){ll num=f(r,i)-f(l-1,i);//计算当前位数的区间1的个数总和if(m[i]==1)num=k-num;//贡献为0的反推出贡献为1的ans+=num;ans%=mod;}cout<<(ans*qmod(k,mod-2))%mod<<endl;//乘法逆元
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)solve();return 0;
}

二进制的规律

1 —— 00001
2 —— 00010
3 —— 00011
4 —— 00100
5 —— 00101
6 —— 00110
7 —— 00111
8 —— 01000
9 —— 01001
10 ——01010
11 —— 01011
12 —— 01100
13 —— 01101
14 —— 01110
15 —— 01111
16 —— 10000
17 —— 10001
18 —— 10010
19 —— 10011
20 —— 10100
通过观察会发现，每一位的周期就是权值的2倍，而权值又是该当前位数的
(2ⁱ ),注意位数i是从0开始的，故而周期为2ⁱ⁺¹ .
至于求余数的贡献值时，会发现在周期的一半的前一位值是1，故而需要多加上1，因为其是余数减去一半的周期。
关键点：

    if(x==0)return 0;ll sum=0;ll val=1ll<<i;//每个周期的贡献值ll curr=1ll<<(i+1);//一个周期的大小ll re=x%curr-val+1;//计算不足一个周期的贡献值sum+=val*(x/curr);//计算整周期的贡献sum+= max((ll)0,re);//比较剩余周期是否有贡献值

相关例题

累加器

题目传送门：累加器


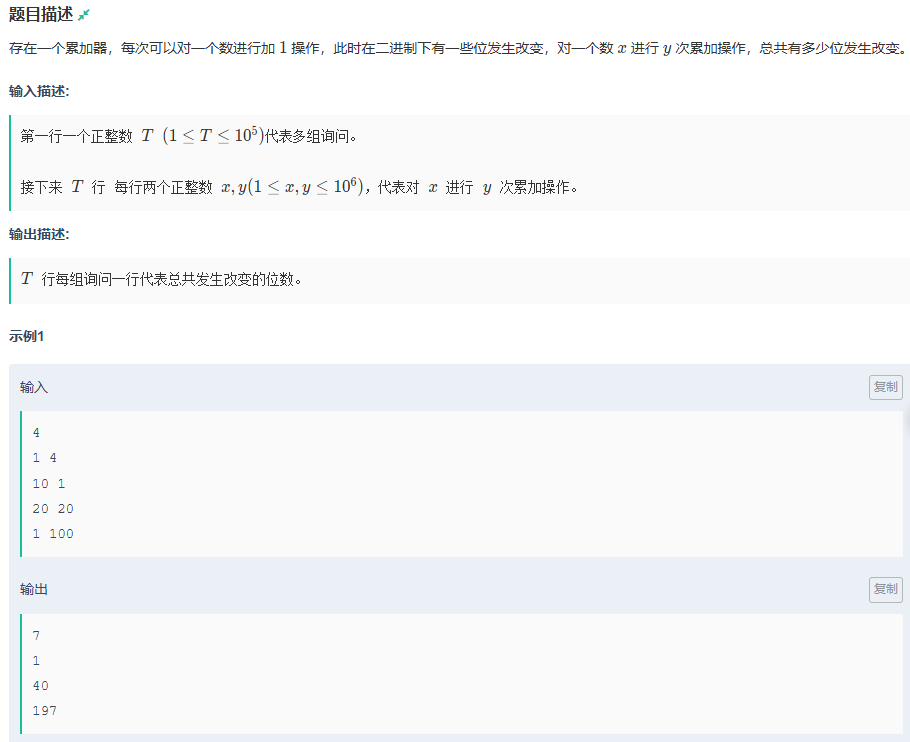
通过观察样例会发现，每位改变的位数，都与当前的2的位数次方
AC代码;

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
const ll N=1e6+10;
ll f(ll x)//进行前缀和
{ll sum=0;ll y=log2(x);for(ll i=0;i<y;i++){ll k=(ll)pow(2,i);//关键规律sum+=x/k;}return sum;
}
void solve()
{ll x,y;cin>>x>>y;cout<<f(x+y)-f(x)<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)solve();return 0;
}

小蓝的二进制询问

题目传送门：小蓝的二进制询问

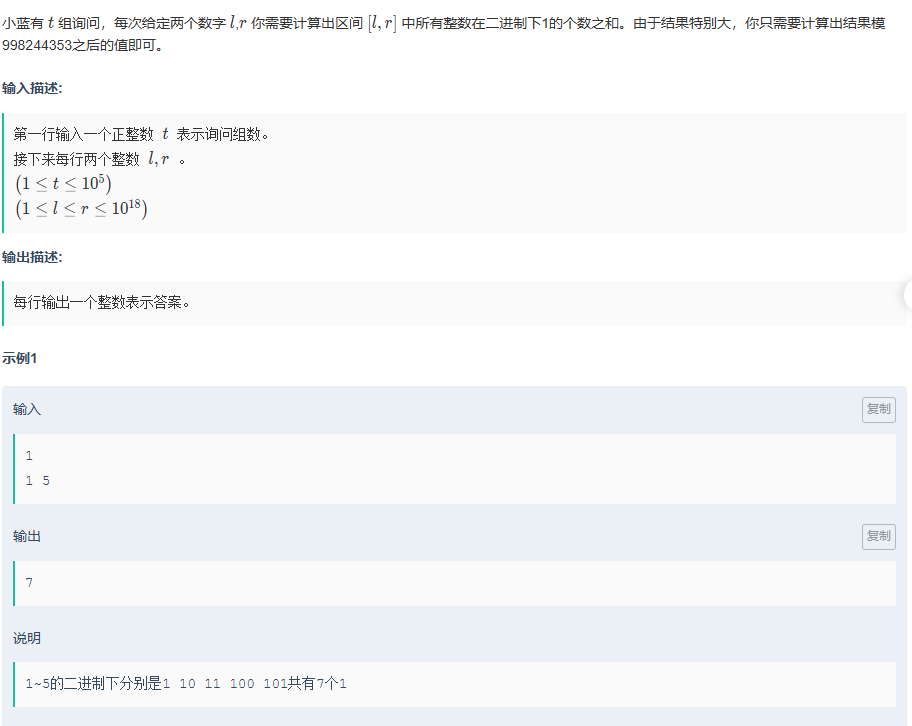
这一题便是之前的规律了；
AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
const ll N=1e6+10;
const ll mod=998244353;
ll f(ll x)
{ll sum=0;ll y=log2(x)+1;//计算当前的位数if(x==0)return 0;ll val=1;for(ll i=0;i<=y;i++){val=1ll<<i;//权值ll curr=val*2;//周期sum+=val*(x/curr);//完整周期总和ll re=x%curr-val+1;//剩余周期的贡献sum+=max((ll)0,re);//判断是否有贡献sum%=mod;}return sum%mod;
}
void solve()
{ll x,y;cin>>x>>y;cout<<(f(y)-f(x-1)+mod)%mod<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)solve();return 0;
}

乘法逆元

1. 概念

在数学中，乘法逆元是一个与乘法运算相关的重要概念，它描述了两个数之间的一种特殊关系。简单来说，对于给定的数 a，如果存在另一个数 b，使得它们的乘积等于乘法单位元（通常是 1），那么 b 就被称为 a 的乘法逆元。

2.基本定义

设 a 是一个数（或更广泛的代数结构中的元素），若存在数 b 满足：$$a\times b=b\times a=1$$
则称 b 是 a 的乘法逆元，记作 $$b=a^{-1}$$（读作 “a 的逆”）。这里的 “1” 是乘法单位元，即与任何数相乘都不改变该数的特殊元素（例如整数乘法中，1 就是单位元）。

3.费马小定理

1.定理内容

若 p 是一个质数，且整数 a 不是 p 的倍数$$（即a与p互质，\gcd (a,p)=1)$$，
则有：$$a^{p-1}\equiv 1(\mathrm{mod}p)$$
符号解释：$$\equiv (\mathrm{mod}p)表示“模p同余”，即a^{p-1}除以p的余数等于1。$$

2.重要推论

费马小定理的一个关键应用是求模运算中的乘法逆元。
由定理 $$a^{p-1}\equiv 1(\mathrm{mod}p)$$
变形可得：$$a\times a^{p-2}\equiv 1(\mathrm{mod}p)$$
这表明：当 p 是质数且 a 与 p 互质时，$$a^{p-2}\mathrm{mod}p$$
就是 a 模 p 的乘法逆元$$（即a^{-1}\equiv a^{p-2}(\mathrm{mod}p)）$$。

根据费马小定理，当 p 是质数且 $$\gcd (a,p)=1时$$，
有：$$a^{p-1}\equiv 1(\mathrm{mod}p)$$
将等式左边因式分解$$（把a^{p-1}拆成a\times a^{p-2}），得到：a\times a^{p-2}\equiv 1(\mathrm{mod}p)$$

D.开罗尔网络的备用连接方案

题目传送门：开罗尔网络的备用连接方案


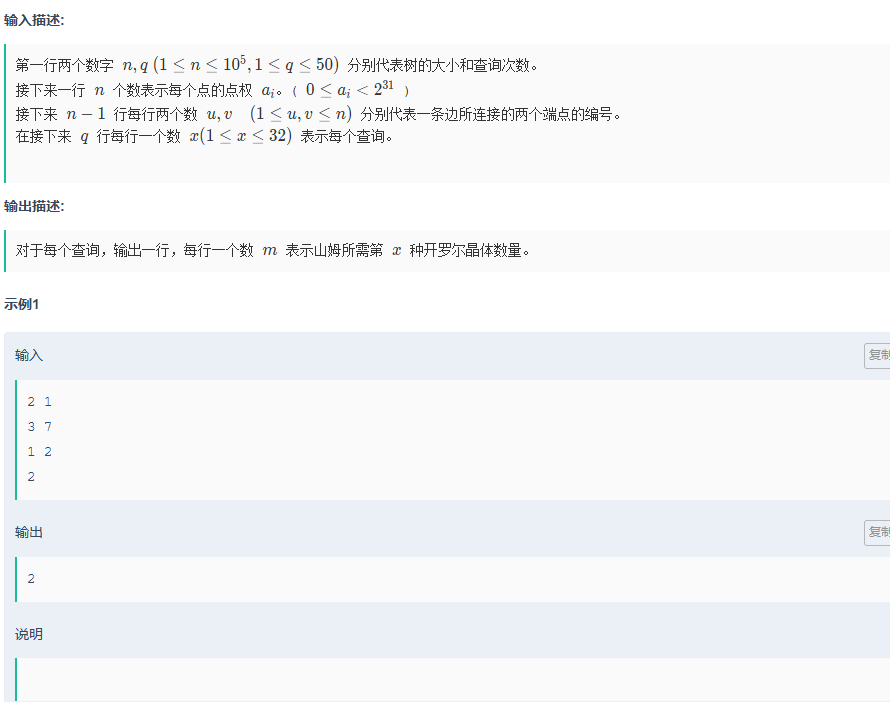
通过题目，可以发现就是一个加权无向图，来求取经过按位与之后该数二进制下1的个数，

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e5+10;
vector<ll> p[N];//用来存边
ll a[N];//存该节点的权值
ll ans[N];//保存种类数目
void dfs(ll x,ll w,ll f)
{ll c=a[x]&w;//每次都进行按位与bitset<40>b(c);//为了更好的求1的个数ans[b.count()]++;//统计种类for(ll i:p[x]){if(i!=f)//防止重边也就是防止一个节点遍历两次{dfs(i,c,x);//继续往下搜索i代表的是子节点，c则是要更新的值，x则代表的是父节点}}
}
void solve()
{ll n,q;cin>>n>>q;for(ll i =1;i<=n;i++)cin>>a[i];for(ll i=1;i<n;i++){ll x,y;cin>>x>>y;p[x].push_back(y);//存边，即双向边p[y].push_back(x);}dfs(1,-1,0);//从节点1开始进行搜索while(q--){ll x;cin>>x;cout<<ans[x]<<endl;}
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;
}

E.咕咕嘎嘎!!!(easy)

题目传送门：咕咕嘎嘎!!!(easy)


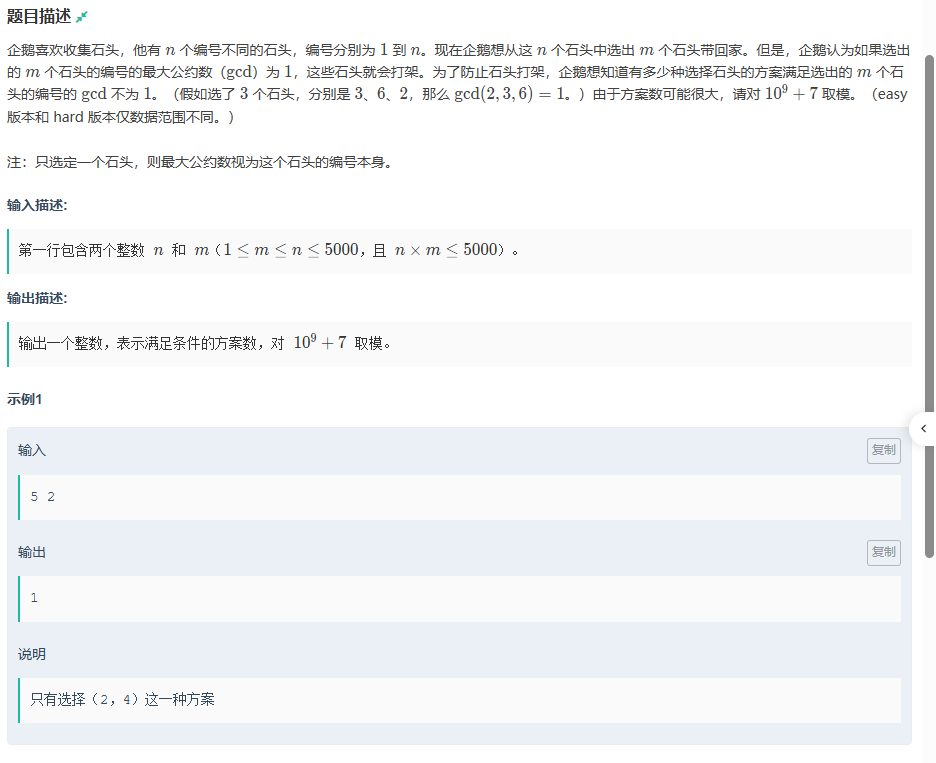
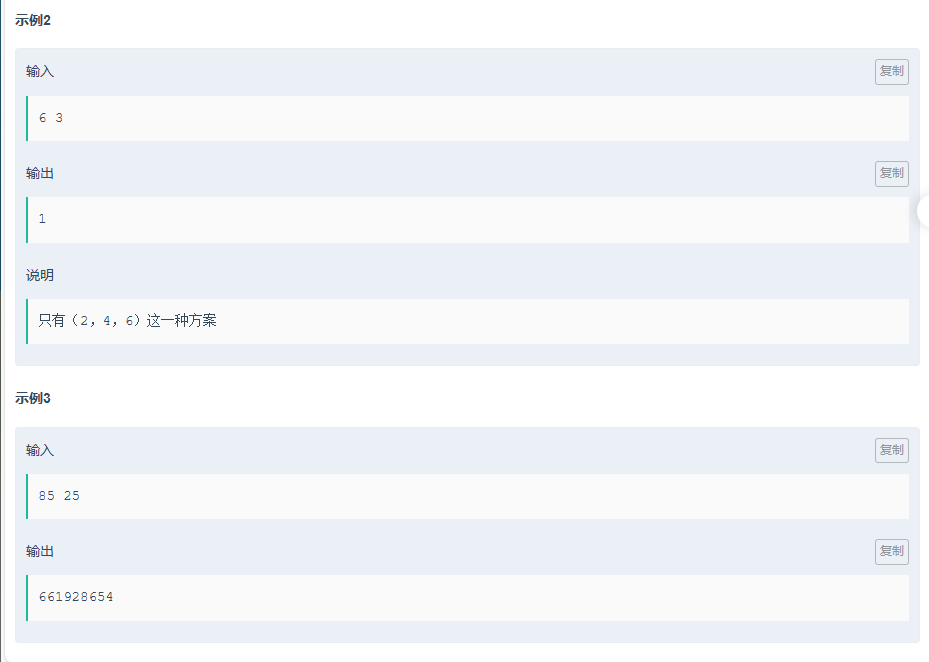
对于这一题，既然最大公因数为1的不满足，那就求出最大公因数大于等于2的。

一、问题转化：补集思想 + 容斥原理
题目要求 选 m 个石头，且它们的 gcd 不为 1 的方案数。直接计算较复杂，采用 补集思想 + 容斥原理 转化问题：
补集思想
总合法方案 = 所有 gcd 为 d（d≥2）的方案数之和。
但直接枚举 d 会重复计算（比如 gcd 为 6 的方案会被 d=2 和 d=3 重复统计），因此需要容斥：从大到小枚举 d，减去其倍数的贡献。
容斥原理
定义 f[d] 为选 m 个石头、且它们的 gcd 恰好为 d 的方案数。
但直接求 f[d] 困难，因此先定义 g[d] 为选 m 个石头、且它们的 gcd 是 d 的倍数（即所有选中的数都是 d 的倍数）的方案数。
则根据容斥关系：$$f[d]=g[d]-\sum _{k>d,d|k}f[k]$$
通过从大到小枚举 d，用 f[d] -= f[k] 的方式实现容斥。
二，预处理：求组合数
递推：s[i][j] = s[i-1][j-1] + s[i-1][j]（选第 i 个元素则从 i-1 选 j-1，不选则从 i-1 选 j）。
这样可以在 O(n^2) 时间内预处理出所有需要的组合数，避免重复计算。
三，核心流程
1. 计算 g[d]：选 m 个 d 的倍数的方案数
对于每个 d（从 1 到 n）：
统计 1~n 中是 d 的倍数的数的个数，记为 num = n / d（因为 d, 2d, 3d, …, kd ≤n → k = n/d）。
若 num ≥ m，则从 num 个数中选 m 个的方案数为组合数 s[num][m]，即 g[d] = s[num][m]；否则 g[d] = 0（不够选 m 个）。

for(ll i=1;i<=n;i++){ll num=n/i;if(num>=m)f[i]=s[num][m];elsef[i]=0;}

2. 容斥修正：从大到小枚举 d
为了得到恰好 gcd 为 d 的方案数 f[d]，需要减去所有 d 的倍数 k=2d, 3d, … 的 f[k]：

for(ll i=n;i>=2;i--) {for(ll j=2*i;j<=n;j+=i) {f[i] = (f[i] - f[j] + mod) % mod;}ans = (ans + f[i] + mod) % mod;
}

从大到小枚举：保证处理 d 时，其倍数 k>d 已经被处理过，这样减去的 f[k] 是 “恰好 gcd 为 k” 的方案数，避免重复计算。
(f[i] - f[j] + mod) % mod：防止负数，用 mod 调整。
AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=5e3+10;
const ll mod=1e9+7;
ll s[N][N];
ll f[N];
void pre()//预处理组合数
{for(ll i=0;i<=N;i++){s[i][0]=0;s[i][i]=1;for(ll j=0;j<i;j++){s[i][j]=(s[i-1][j-1]+s[i-1][j]+mod)%mod;}}
}
void slove()
{ll n,m;cin>>n>>m;ll ans=0;for(ll i=1;i<=n;i++){ll num=n/i;//1~n中i的倍数的个数if(num>=m)// 若数量足够选m个f[i]=s[num][m];elsef[i]=0;}// 第二步：容斥原理计算f[d] = 选m个数且gcd恰好为d的方案数// 从大到小枚举d，确保处理d时其倍数已被处理for(ll i=n;i>=2;i--){// 减去所有i的倍数的f[j]（这些是gcd为j的方案，已被包含在g[i]中）for(ll j=2*i;j<=n;j+=i){f[i]=(f[i]-f[j]+mod)%mod;}// 累加所有gcd≥2的方案数ans=(ans+f[i]+mod)%mod;}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;pre();// cin>>t;while(t--)slove();return 0;
}

I.猜数游戏(easy)

题目传送门：猜数游戏(easy)

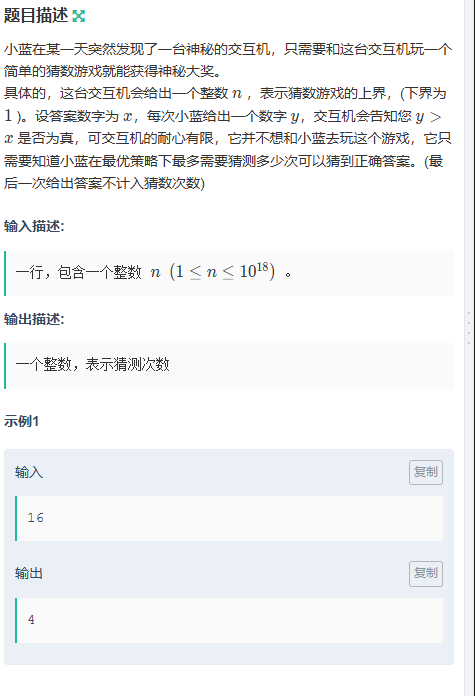
签到题没啥说的
AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll ans=0;
void solve()
{ll n;cin>>n;ll sum=1;while(sum<=n){sum*=2;ans++;}if(sum/2==n)cout<<ans-1<<endl;elsecout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

K.打瓦

题目传送门：打瓦

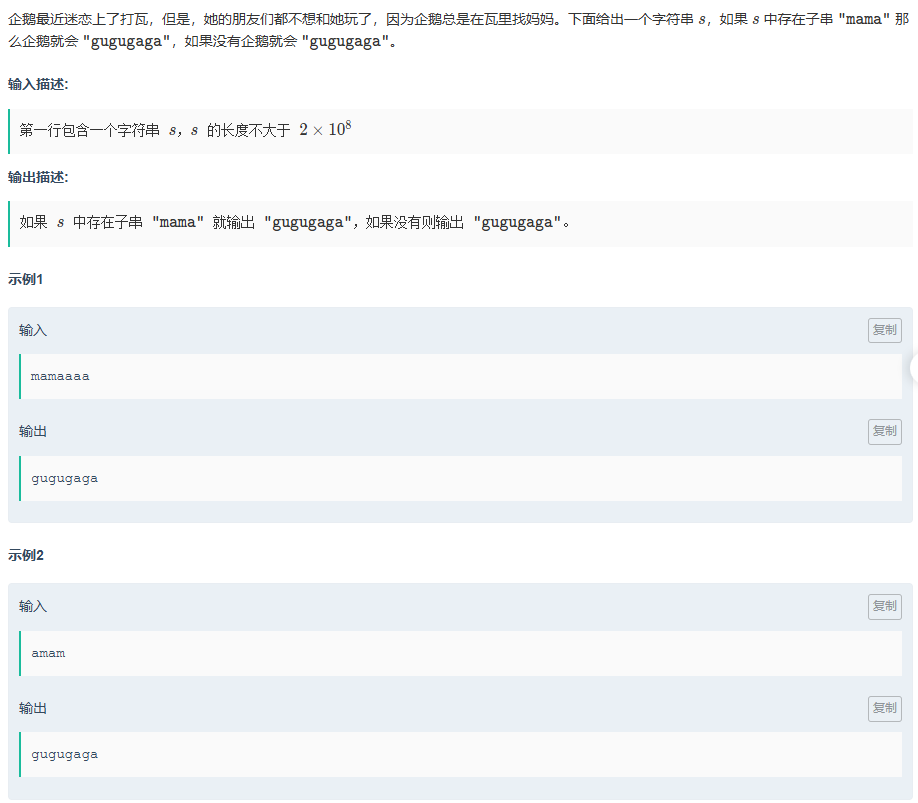
同样签到题
AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
void solve()
{string s;cin>>s;cout<<"gugugaga"<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

M.米娅逃离断头台

题目传送门：米娅逃离断头台


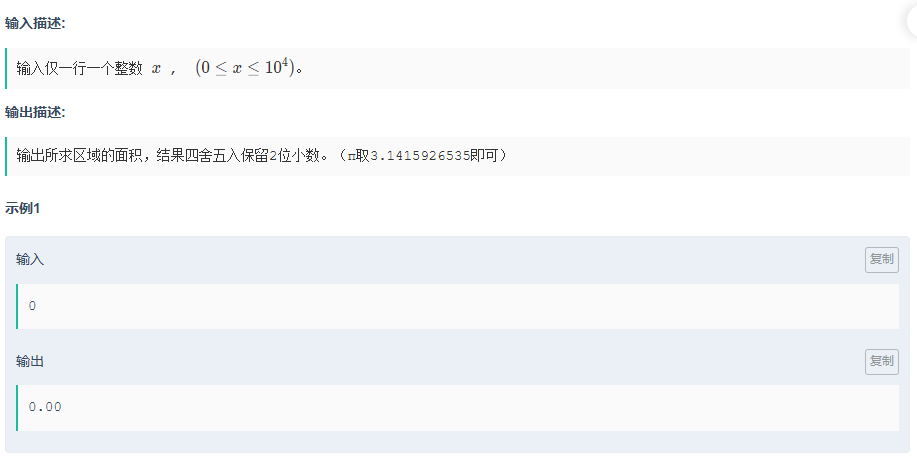
简单的数学题
AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
double x;
void solve()
{cin>>x;double sum=3.1415926535;double ans=0;if(x==0){printf("0.00\n");return ;}else{ans=(sum*x*x)/8;printf("%.2lf\n",ans);}
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

总结

对于其他题，尤其a题就是属于没思路的一题
而D题，才开始题目没看太懂，没有建立无向边，建立的是有向边，等到后续给了题目更近一步的解释时，越来越迷糊，图论还是接触的少。