伯努利模型的参数估计方法

1. 统计学习方法三要素对比

方法	模型	策略	算法
极大似然估计	概率模型	经验风险最小化	数值解
贝叶斯估计	概率模型	结构风险最小化	解析解

2. 极大似然估计

2.1 模型设定

设$P(x=1)=\theta$，则$P(x=0)=1-\theta$

2.2 似然函数

对于n次独立实验，k次结果为1：

$$L(x_1,x_2,...,x_n;\theta )={\theta }^k(1-\theta {)}^{n-k}$$

2.3 对数似然函数

$$\ln L=k\ln \theta +(n-k)\ln (1-\theta )$$

2.4 求导得估计值

$${\hat{\theta }}_{MLE}=\frac{k}{n}$$

Python实现

import numpy as np
from scipy.stats import bernoulli# 生成伯努利数据
np.random.seed(42)
theta_true = 0.7
n = 1000
data = bernoulli.rvs(theta_true, size=n)
k = sum(data)# 极大似然估计
theta_mle = k / n
print(f"MLE估计值: {theta_mle:.4f}")

LE估计值: 0.7120

3. 贝叶斯估计

3.1 先验分布选择

使用Beta分布作为共轭先验：

$$f(\theta ;\alpha ,\beta )=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}{\theta }^{\alpha -1}(1-\theta {)}^{\beta -1}$$

3.2 后验分布

后验分布也是Beta分布：

$$f(\theta |D)\propto {\theta }^{k+\alpha -1}(1-\theta {)}^{n-k+\beta -1}$$

3.3 MAP估计

$${\hat{\theta }}_{MAP}=\frac{k+\alpha -1}{n+\alpha +\beta -2}$$

from scipy.stats import beta# 设置先验参数 (α=2, β=2 相当于均匀分布)
alpha, beta_ = 2, 2# MAP估计
theta_map = (k + alpha - 1) / (n + alpha + beta_ - 2)
print(f"MAP估计值: {theta_map:.4f}")# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 使用微软雅黑字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号'-'显示为方块的问题
# 后验分布可视化
import matplotlib.pyplot as plt
theta_range = np.linspace(0, 1, 1000)
posterior = beta.pdf(theta_range, k+alpha, n-k+beta_)
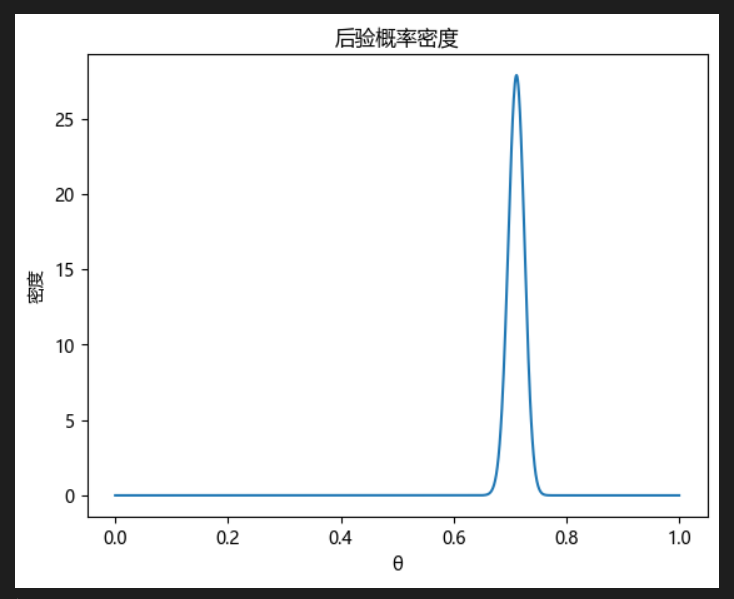
plt.plot(theta_range, posterior)
plt.title('后验概率密度')
plt.xlabel('θ')
plt.ylabel('密度')
plt.show()

4. 经验风险最小化与极大似然估计的关系

当满足以下条件时，经验风险最小化等价于极大似然估计：

1. 模型是条件概率分布
2. 损失函数是对数损失函数

4.1 经验风险最小化形式

$$\min \frac{1}{N}\sum _{i=1}^N-\ln P(Y_i|X_i,\theta )$$

4.2 等价于极大似然

$$\max \prod _{i=1}^{N}P(Y_i|X_i,\theta )$$

注意事项

1. 选择先验分布时需注意定义域匹配
2. Beta分布是伯努利分布的共轭先验
3. 当先验为均匀分布时，MAP估计退化为MLE估计

# 模拟广告点击数据 (10个广告，每个展示1000次)
np.random.seed(42)
ctr_true = np.linspace(0.1, 0.9, 10)
clicks = [np.sum(bernoulli.rvs(p, size=1000)) for p in ctr_true]# 使用贝叶斯估计平滑小CTR
alpha, beta_ = 5, 95  # 先验认为点击率约5%
smoothed_ctr = [(c + alpha)/(1000 + alpha + beta_) for c in clicks]# 可视化对比
plt.figure(figsize=(10,5))
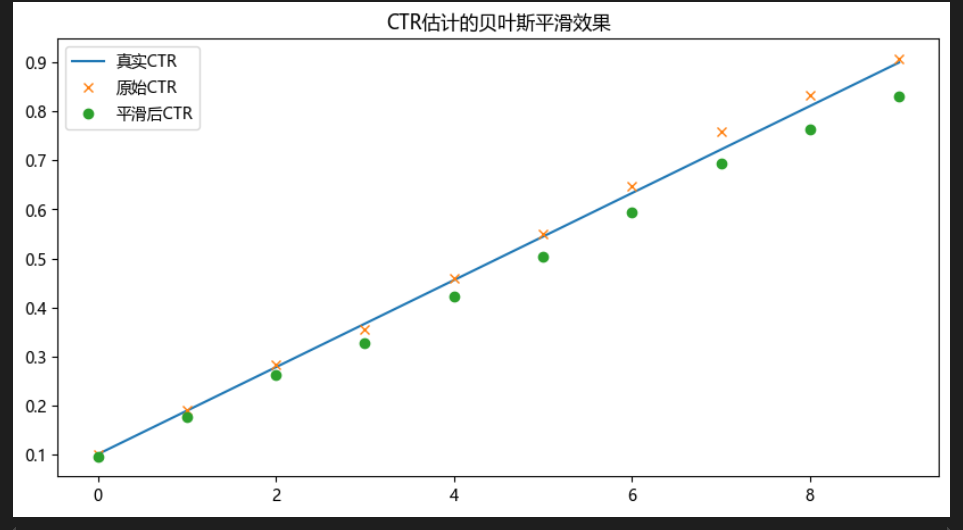
plt.plot(ctr_true, label='真实CTR')
plt.plot([c/1000 for c in clicks], 'x', label='原始CTR')
plt.plot(smoothed_ctr, 'o', label='平滑后CTR')
plt.legend()
plt.title('CTR估计的贝叶斯平滑效果')
plt.show()