此练习,主要是使用状态空间方程来设计控制器的方法和思路:
①系统建模;
②系统的能控性;
③极点配置;
④最优化控制LQR;
⑤轨迹追踪;
以下是,第①部分:系统建模;
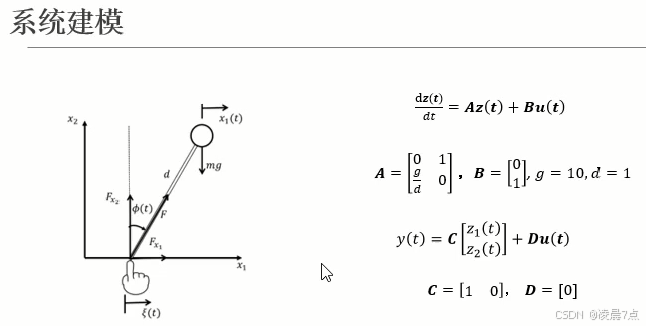
一、系统模型
- 以下图,连杆小球的例子;
- 系统仿真参数:重力加速度g=10、连杆长度d=1;
- 状态变量z1(t)定义为:连杆小球与垂直位置的角度;
- z2(t)为:就是z1(t)的导数,即是角速度;
- 系统输出y(t)定义为:连杆小球与垂直位置的角度,也就是z1(t);
clc;clear;close all;
%% 定义参数g=10;d=1;
%% 定义矩阵A=[0 1;g/d 0];B=[0;1];C = [1, 0];D = 0;
%% 建立状态空间方程表达式
sys = ss(A,B,C,D);
%% 定义初始状态
z0=[pi/20;0]; % 就是连杆小球与垂直位置的,初始角度是pi/20;角速度是0;
%% 对初始状态的响应
t=0:0.01:20;
[y,t,z]=initial(sys,z0,t);% initial就是对初始条件的响应,z0状态变量
plot(t,z(:,1));
hold on;
plot(t,z(:,2));
grid on;
legend('角度:z1(t)','角速度:z2(t)');
hold off;
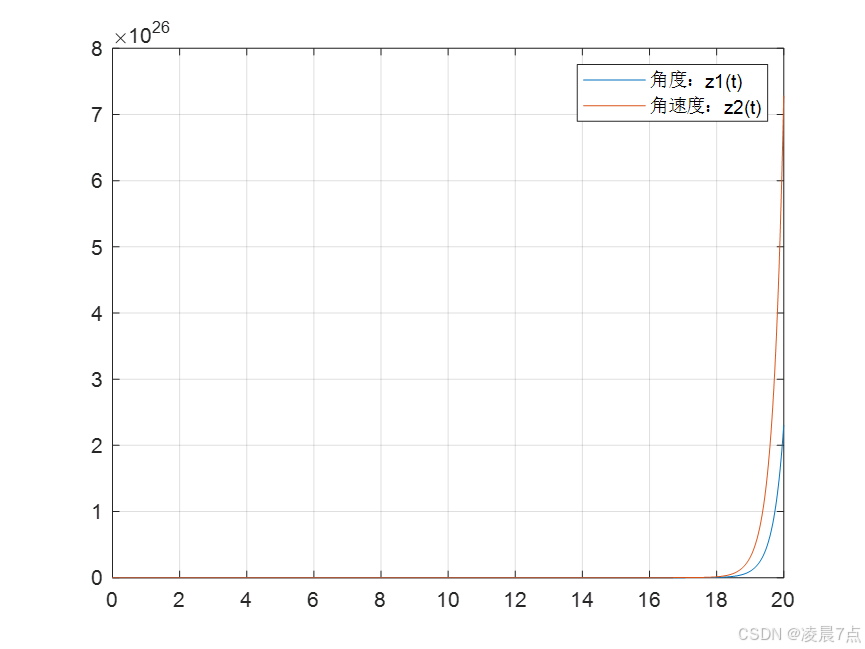
二、运行结果
- 从图看出;两个状态变量都趋向于无穷;
- 因为,此时没加任何的输入u=0,所以当小球偏离了平衡位置,是不会自己回去的,角度和角速度就是越变越大的;
- 因此,需要设计合适的控制器,来稳定平衡连杆小球。
学习来源:《控制之美》[卷1],王天威



(1天))


)









进行文件上传漏洞渗透实战分析)

)
