---

前言

近日，我有幸深入学习了国防科技大学吕欣教授及其团队所著的《数据挖掘》一书，深受启发，收获颇丰。这本书系统性地介绍了数据挖掘的核心理论与经典算法，内容既涵盖基础概念，又深入实战技巧，尤其适合机器学习、数据科学领域的初学者和进阶者阅读。

吕欣教授及其团队以其深厚的学术功底和丰富的实践经验，将复杂的数据挖掘知识讲解得条理清晰、通俗易懂。书中不仅有严谨的数学推导，还配有丰富的案例和代码实现，真正做到了理论与实践相结合。

为更好地消化吸收书中精华，我将持续更新《集成学习》章节的读书笔记，内容包括集成学习的基本思想、常见方法（如Bagging、Boosting、Stacking）、随机森林、AdaBoost、GBDT、XGBoost以及LightGBM等核心算法的原理、实现与调参技巧。希望能帮助更多同学系统掌握集成学习的知识体系，也为大家在学习《数据挖掘》这本书时提供一份参考资料。

如果你对数据挖掘、机器学习感兴趣，或正在寻找一本既能打基础又能提升实战能力的教材，吕欣教授的《数据挖掘》绝对是不可多得的好书。推荐给大家！

下面是我的读书笔记正文，欢迎交流指正👇

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、集成学习是什么？

1.基本思想

（1）“弱者的联盟”

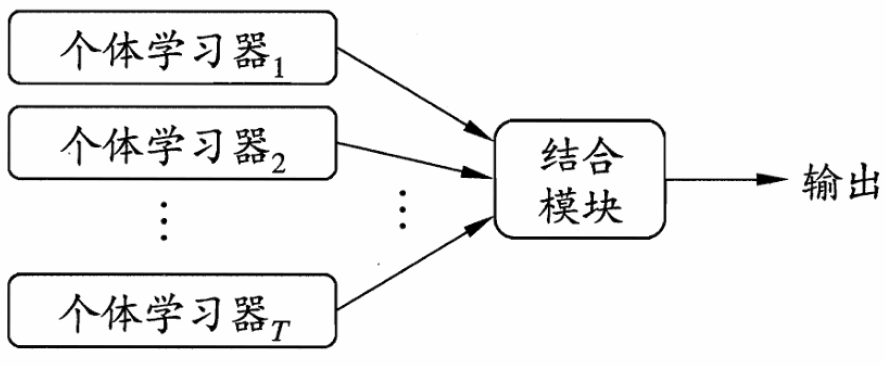
集成学习(Ensemble learning)是机器学习中的一种思想，通过构建并结合多个个体学习器（Individual learner）形成一个精度更高的机器学习模型。这些个体学习器也是机器学习算法，可以是朴素贝叶斯、决策树、支持向量机和神经网络等。集成学习示意图如图1所示。

传统机器学习算法 (例如：决策树，逻辑回归等) 的目标都是寻找一个最优分类器尽可能的将训练数据分开。集成学习 算法的基本思想就是将多个弱分类器组合，从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话：三个臭皮匠，赛过诸葛亮。

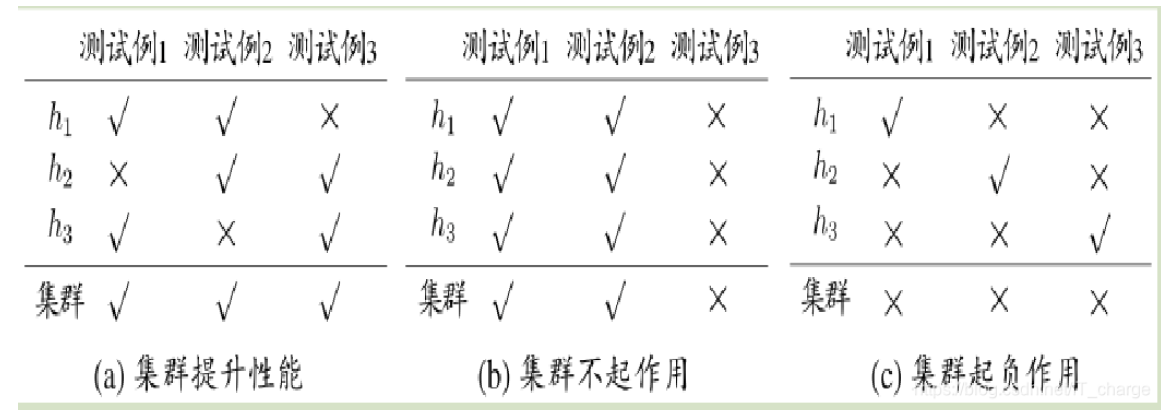
（2）“多样性红利”：模型间的差异性比单个模型的精度更重要，这与人类社会团队协作的规律惊人相似。

2.集成学习的类型

3. 集成学习的结合策略

3.1 为什么结合策略是集成学习的灵魂？

集成学习的核心不是“模型越多越好”，而是“如何让模型间的协作产生超越个体的智
慧”。真正决定集成效果上限的，往往是基学习器的结合策略（Combination Strategy）。

[!NOTE]

我的思考：

• 如果把基模型比作“专家”，结合策略就是“专家委员会”的议事规则；

• 好的策略能抑制噪声、放大有效信息，甚至让弱模型通过协作达到强模型的效果；

• 结合策略的设计本质是信息融合的数学建模，背后隐含对数据分布、模型能力的先验假设。

3.2 经典策略

(1)投票法（Voting）

• 硬投票（Hard Voting）：平等对待每个模型，易受“多数暴政”影响（噪声模型可能主导结果）

$$\hat{y}={\mathrm{argmax}}_{c\in C}\sum _{i=1}^T\mathbb{I}(h_i(x)=c)$$

​ 其中：

​ C：类别集合; II(⋅)：指示函数（预测为类别 cc 时取1，否则取0）。

​ 特点:直接统计类别票数，多数决制；可能受“多数噪声模型”干扰（若多个弱模型预测错误）。

---

• 软投票（Soft Voting）：引入概率权重，但对置信度的校准敏感（模型输出概率未必可靠）。

$$\hat{y}={\mathrm{argmax}}_{c\in C}\frac{1}{T}\sum _{i=1}^T{P}_i(c|x)$$

​ 其中：

• $$P_i(c|x)表示第i个模型对样本x属于类别c的预测概率。$$

​ 特点：要求基模型能输出概率（如逻辑回归、带概率校准的SVM）；对模型校准敏感，若概率未校准可能效果下降。

---

• 加权投票（Weighted Voting）

​ 以软投票为例：
$$\hat{y}={\mathrm{argmax}}_{c\in C}\sum _{i=1}^T{w}_i{P}_i(c|x)$$

• 权重wi可基于模型性能或领域知识设定（如AUC值高的模型权重更大）。

[!NOTE]

• 是否所有模型的“投票权”应该平等？
• 如何量化模型在不同样本区域的置信度？
• 改进思路：动态权重分配（如基于样本局部密度的加权投票）。

(2)平均法（Averaging）

• 简单平均（Simple Averaging）
  $$\hat{y}=\frac{1}{T}\sum _{i=1}^T{h}_i(x)$$
  其中：T：基模型数量；h_i(x)：第 i 个模型对样本 x 的预测值；y^：最终预测结果。

​ 特点：所有模型权重相等，假设模型误差服从独立同分布；对异常值敏感（可通过截断平均改进）。

• 加权平均（Weighted Averaging）
  $$\hat{y}=\sum _{i=1}^T{w}_i{h}_i(x),\text{其中}\sum _{i=1}^T{w}_i=1$$
  wi：第i个模型的权重，通常根据模型性能（如验证集准确率）动态分配。

  特点：高性能模型获得更高权重；需注意权重分配的合理性（避免过拟合验证集）。

[!TIP]

• 算术平均假设误差服从高斯分布，但现实任务中误差可能呈现偏态或重尾分布。

• 案例：在金融风险预测中，少数极端值的预测误差可能对简单平均产生灾难性影响。

• 解决方案：

  截断平均（Trimmed Mean）：去掉最高/最低的预测值；

  分位数融合（Quantile Blending）：直接集成不同分位数的预测结果。

(3) 学习法

• 传统Stacking用基模型的输出训练元模型，但可能引入过拟合风险（尤其在基模型高度相关时）。
• 我的实验发现：
  • 使用低复杂度的元模型（如线性回归）反而比深度网络更稳定；
  • 对基模型输出做特征工程（如加入原始特征、交互项）比直接拼接更有效；
  • 对抗验证技巧：通过检测元模型是否过拟合基模型的噪声来调整训练策略。

---

3.3 关键对比与选择建议

方法	适用场景	优点	缺点
简单平均	模型性能相近的回归任务	计算简单，抗过拟合	对异常值和低质量模型敏感
加权平均	模型性能差异显著的回归任务	灵活利用模型差异性	需额外计算权重，可能过拟合验证集
硬投票	类别标签明确的分类任务	无需概率输出，实现简单	忽略模型置信度，易受多数噪声影响
软投票	模型输出可靠概率的分类任务	利用概率信息，结果更平滑	依赖概率校准，计算复杂度略高

---

总结

以上就是今天要讲的内容，通过对吕欣老师《数据挖掘》教材中“集成学习”章节的系统学习与梳理，我对这一强大机器学习范式的核心思想和方法论有了更深刻的认识。

1. 核心思想：协作优于单干
   集成学习的魅力在于其朴素而深刻的哲学：“弱者的联盟”。它通过构建并结合多个性能尚可的“弱学习器”，最终形成一个预测更精准、泛化能力更强的“强学习器”。这完美印证了“三个臭皮匠，赛过诸葛亮”的古老智慧。其成功的核心关键并非个体模型的极致性能，而在于模型之间的“多样性”，即模型误差的差异性和互补性。

2. 方法论的三大支柱：
   集成学习主要围绕三大策略展开，各有其独特的工作机制与适用场景：
   (1) Bagging (如随机森林)：通过并行 Bootstrap 抽样构建多个基学习器，并采用投票/平均法结合结果。其核心是降低方差，通过“民主决策”来平滑噪声、避免过拟合。
   (2) Boosting (如AdaBoost, GBDT)：通过串行方式训练基学习器，每个新模型都专注于修正前序模型的错误，并动态调整样本权重。其核心是降低偏差，体现“知错能改”，逐步逼近复杂问题。
   (3) Stacking：引入“元学习器”来学习如何最优地组合多个基学习器的预测结果，如同一个“专家委员会”的决策机制，灵活性最高，但需谨慎防止过拟合。

3. 结合策略是灵魂：
   如何将多个模型的输出转化为最终决策，是集成学习的精髓。投票法（硬投票、软投票）和平均法（简单平均、加权平均）是直观的策略，而其背后蕴含的是对模型置信度、性能差异以及误差分布的深刻考量。

总而言之，集成学习不仅是数据挖掘工具箱中一套高效且实用的算法集合，更是一种解决问题的系统性思维——通过协作与组合，将有限的个体能力汇聚成强大的集体智慧。吕欣教授的《数据挖掘》一书对此进行了极为清晰和富有洞见的阐述，极大地帮助我构建了系统性的知识框架，特此推荐给每一位对机器学习感兴趣的朋友。

作者：栗子同学、李同学