加法器是数字电路中用于执行加法运算的基本逻辑单元，广泛应用于计算机、计算器、数字信号处理器等电子设备中。它能将两个二进制数相加，并输出结果及可能产生的进位。
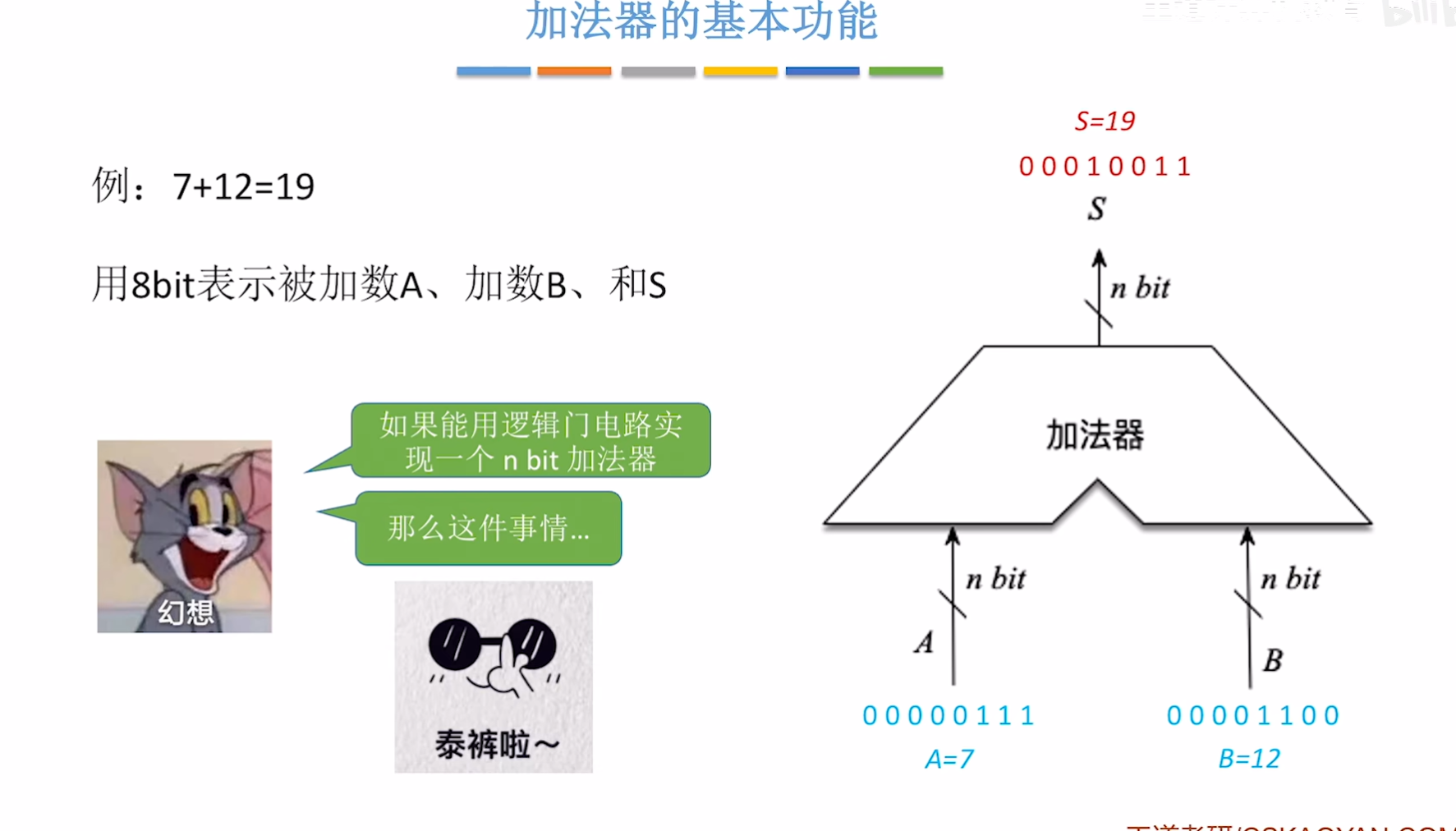
一、加法器的基本功能
加法器的基本功能是在数字电路中对输入的二进制数执行加法运算，具体可从以下几个核心层面理解：
- 核心运算：对两个二进制数字（通常是 0 或 1）进行相加，输出运算结果。这一过程遵循二进制加法规则：0+0=0、0+1=1、1+0=1、1+1=0（同时产生进位 1）。
- 处理进位：根据设计不同，可处理运算中产生的进位信息：
- 半加器：仅对两个 1 位二进制数相加，输出本位和与向高位的进位，但不考虑来自低位的进位。
- 全加器：在两个 1 位二进制数相加的基础上，额外接收来自低位的进位输入，最终输出本位和与向高位的进位输出，完整处理三级输入（两个加数 + 低位进位）的加法逻辑。
- 扩展运算：通过多个加法器级联（如串行进位加法器、超前进位加法器），可实现多位二进制数的加法，满足对更大数值（如 8 位、16 位、32 位等）的运算需求，为计算机、计算器等设备的算术功能提供基础支持。
二、如何用门电路实现一位加法？
大家如果还有不理解的可以去看B站看王道考研去琢磨一下，第一次的时候可能难以理解，多琢磨琢磨，可以思考下为什么会有与 或 异或 同或这四种逻辑运算？然后在根据他们的运算法则理解电路
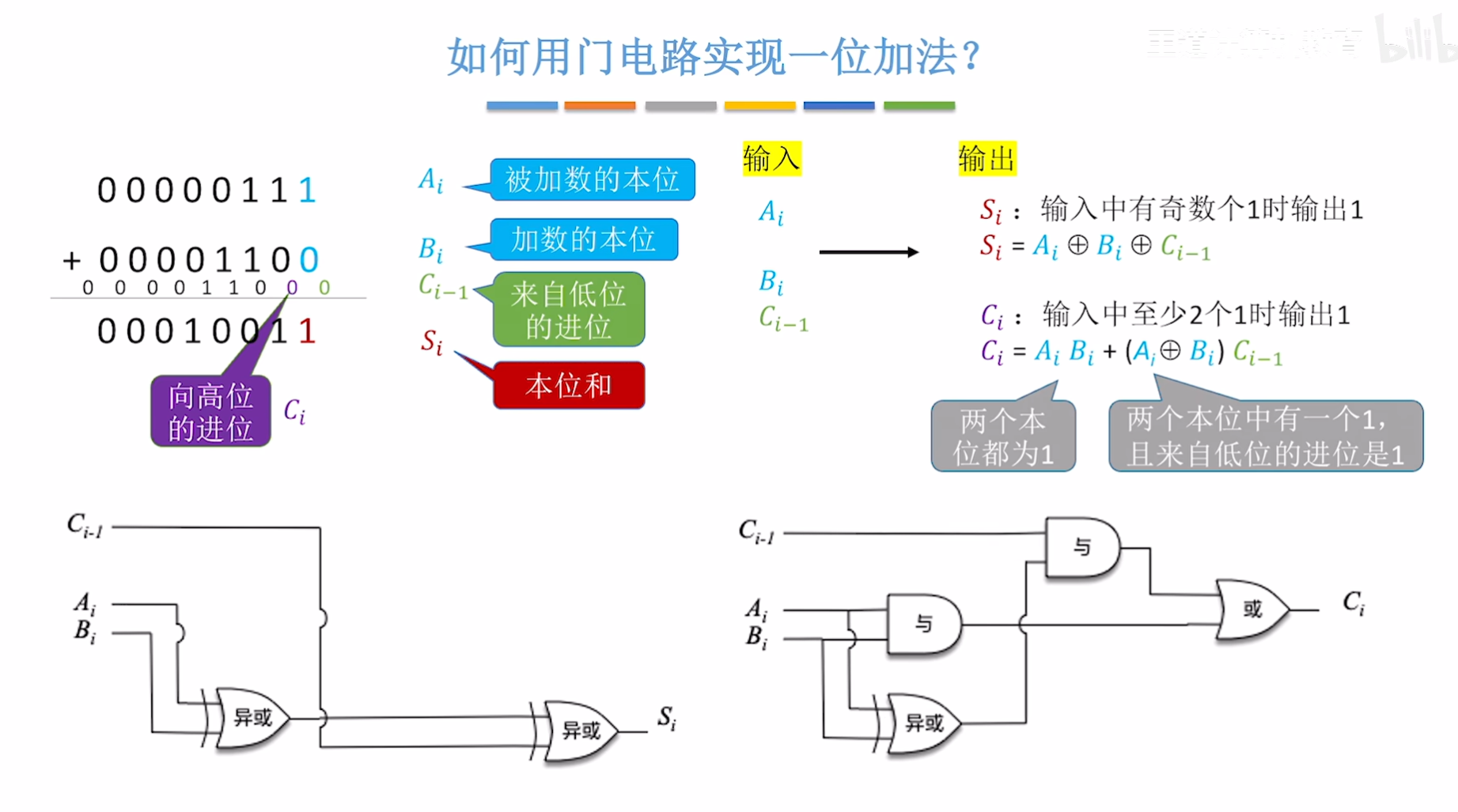
功能：对两个 1 位二进制数（A、B）和来自低位的进位（C_in）进行加法，输出本位和（Sum）与向高位的进位（C_out）。
逻辑分析：
- 求和（Sum）：三个输入（A、B、C_in）中 “1” 的个数为奇数时结果为 1（可通过两次异或实现）。
- 进位（C_out）：三个输入中至少两个为 1 时产生进位 1（可通过与门和或门组合实现）。
门电路实现：
求和：
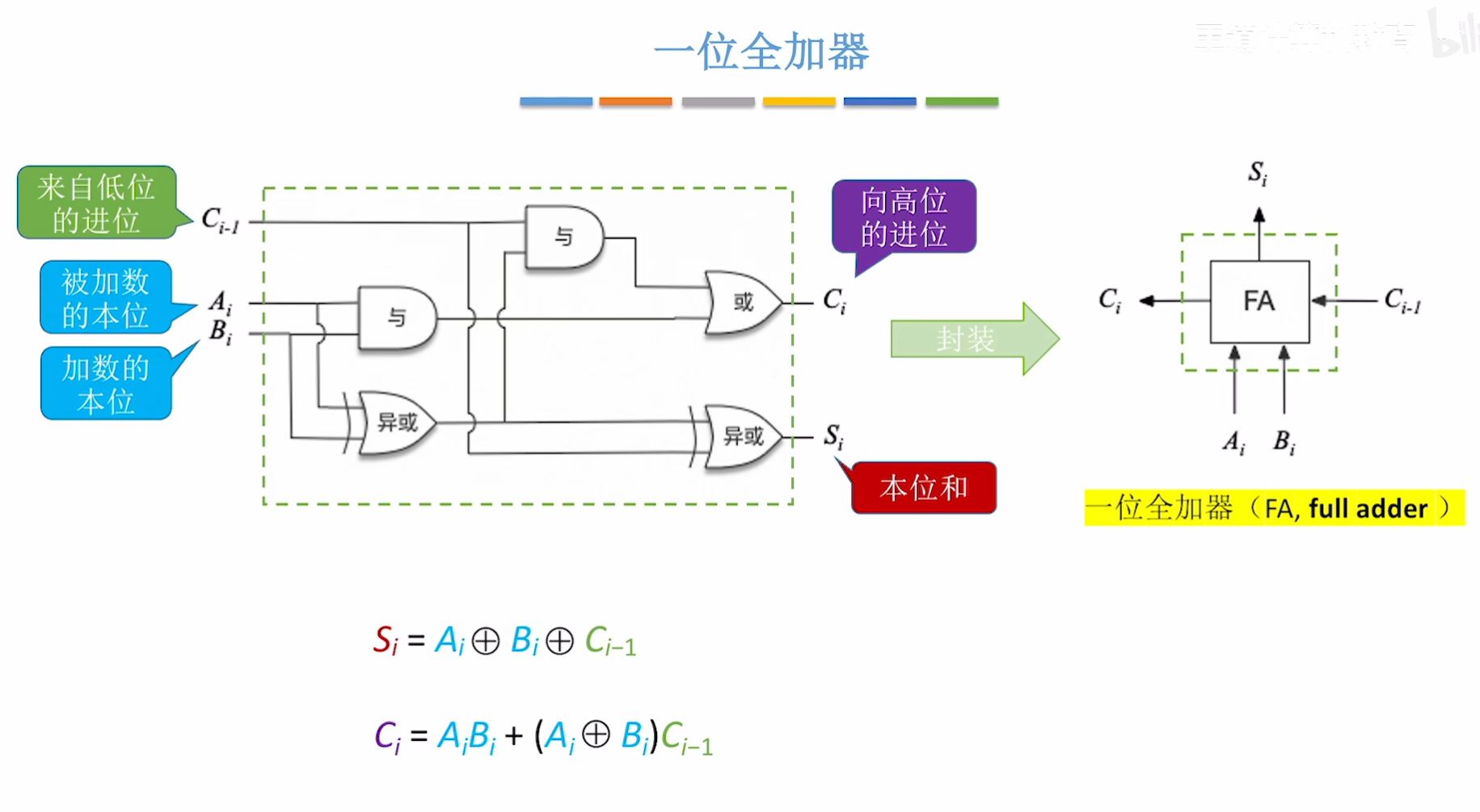
Sum = (A ⊕ B) ⊕ C_in
（先用异或门处理 A 和 B，再将结果与 C_in 通过异或门）进位：
C_out = (A · B) + (A · C_in) + (B · C_in)
（三个与门分别处理 A&B、A&C_in、B&C_in，再通过或门合并结果）
三、 一位全加器
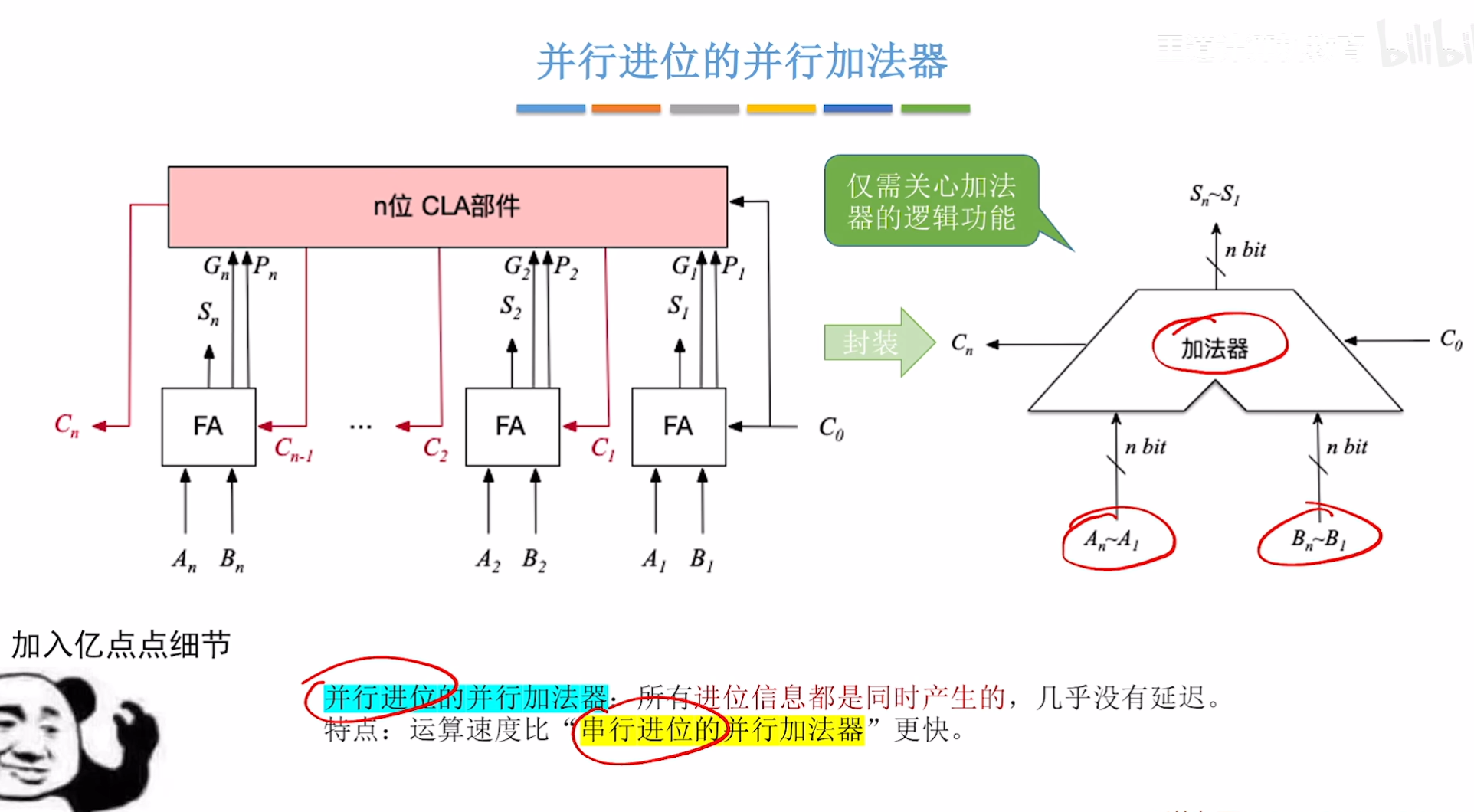
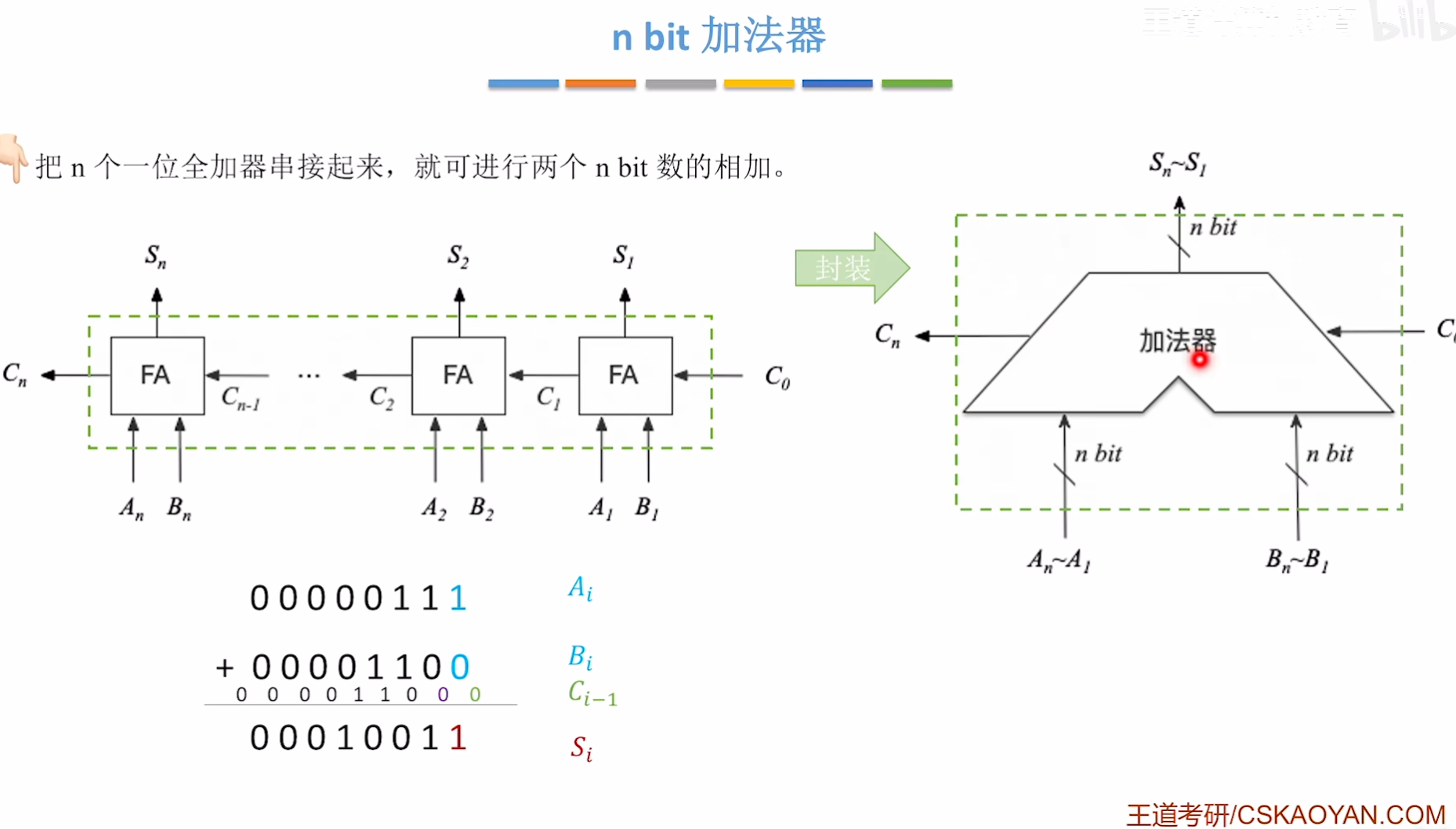
四、n bit 全加器
不足之处： 串行的计算速度取决于进位和传递的速度，所以根据技术的发展，这种肯定是不可以用的，我们需要一个并行的加法器
五、带标志位的加法器
在实际的运行过程中，我们的运算一定是正确的么？ 不一定的，出错了硬件应该发现这种问题，所以又有了带标志位的加法器
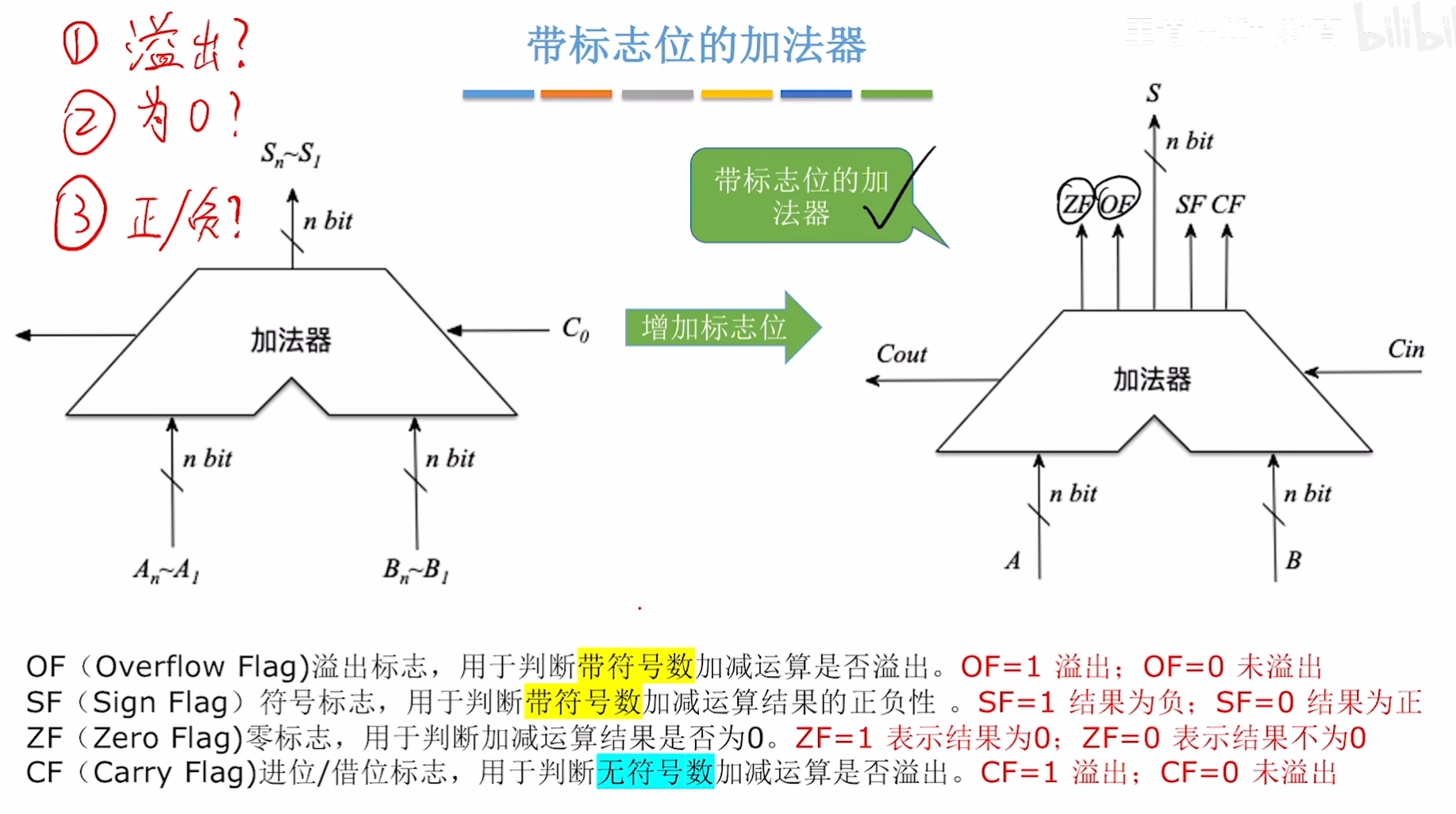
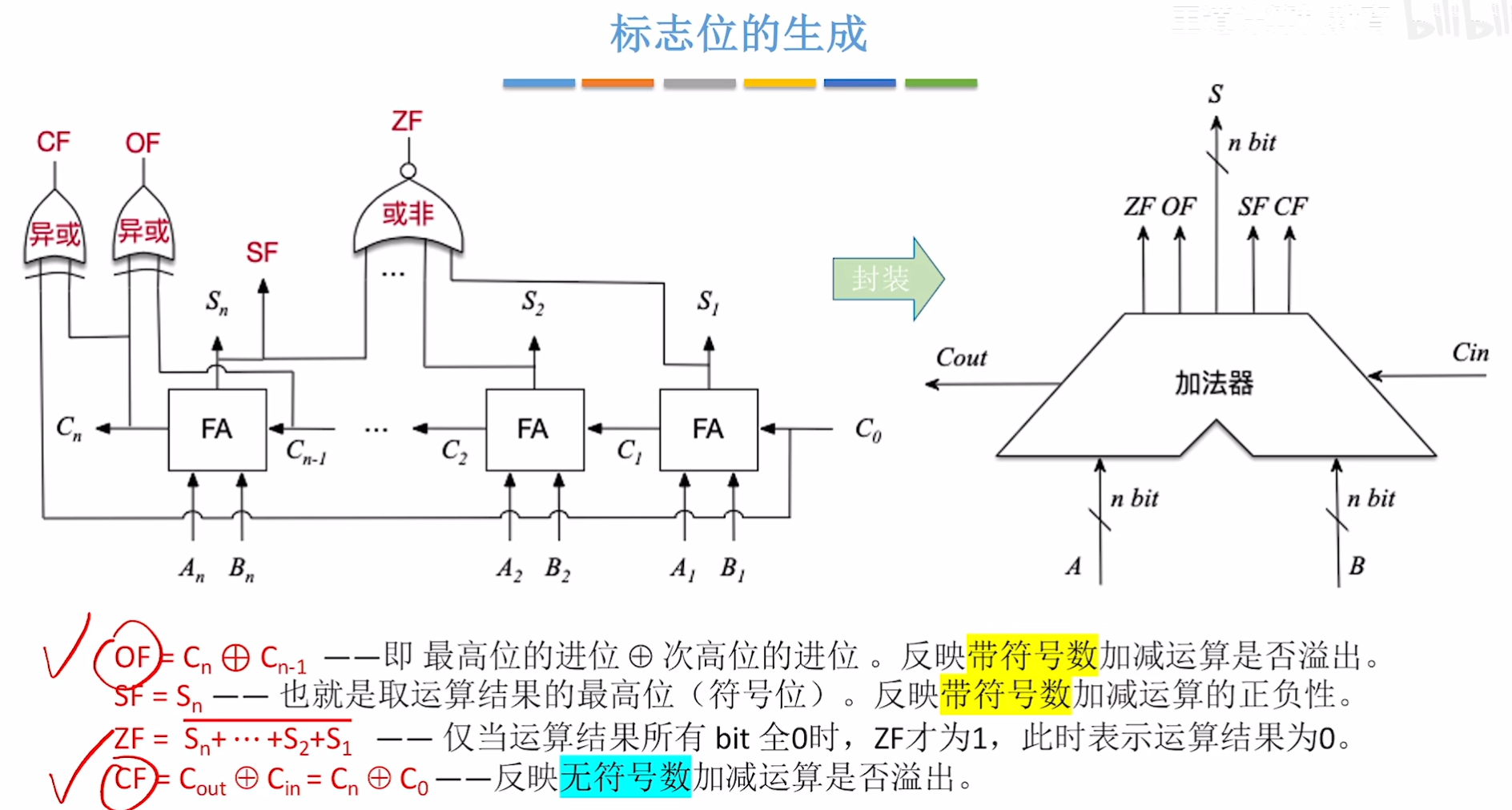
1. 标志位的生成
标志位是怎么生成的呢，大家可以了解下下面的图，稍微了解即可，我们并不需要关心里面的细节
六、 总结
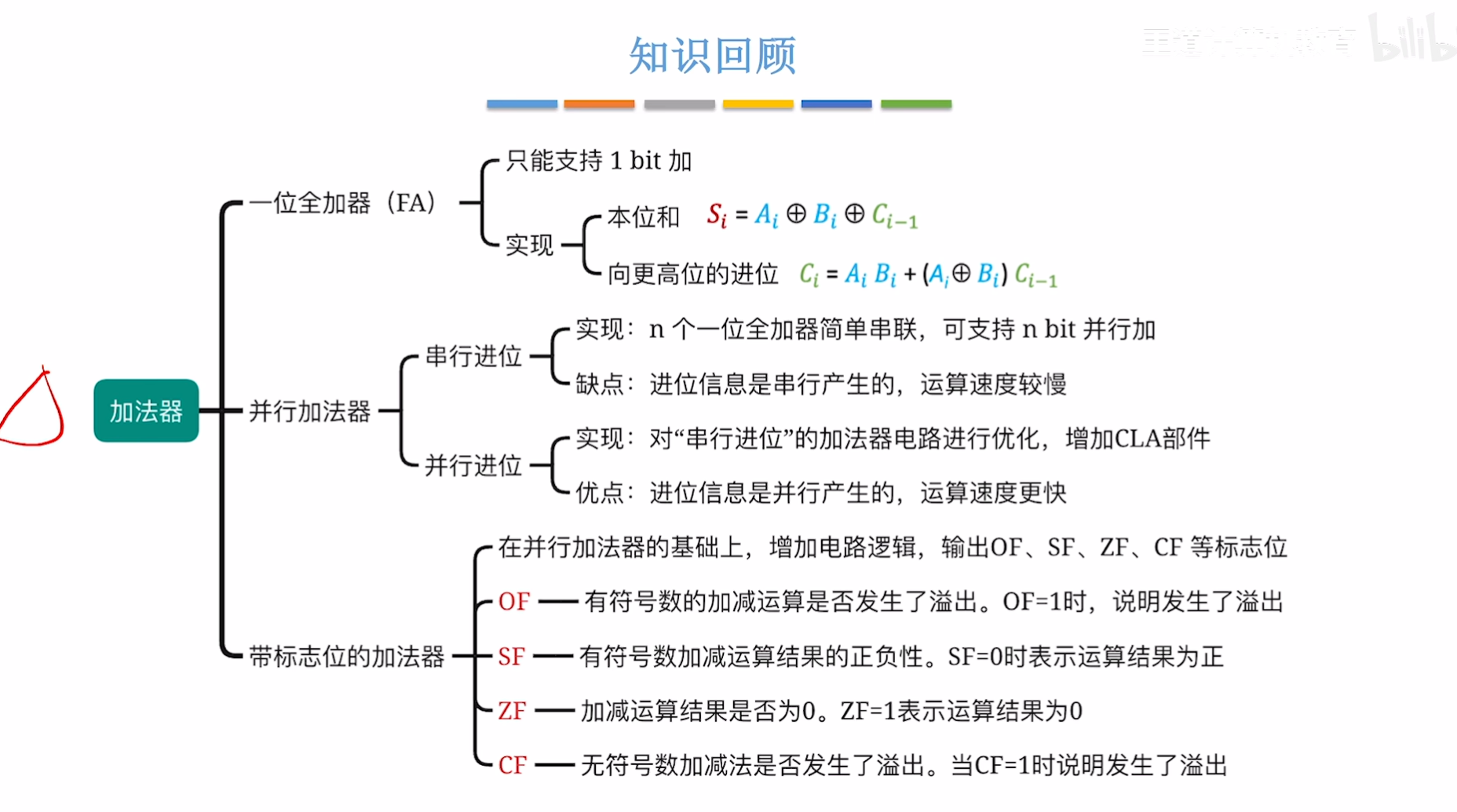这里大家了解即可，实际我们的开发过程中只需要清楚CPU 内加法器的工作原理，我们并不需要知道他的工作细节是什么，除非你要考研，你搞的这么6，是要考研么!, 那另当别论。
我只是了解了下其中的工作原理，有一个很有意思的思考，就是与 或 异或 同或的这四个逻辑运算的思考。
