目录
前言
一、基础知识
二、NCC基本公式以及解决问题
1. NCC基本公式
2. 基本公式解读
三、简化分母 fuv
1. 要简化的分母
2. 积分图
3. 分母拆开化简
四、简化分子
1. 要简化的分子
2. 模板函数的近似
3. 基函数简单解释
五、Fast NCC归一化互相关值
1. 最终公式
2. 复杂性对比
3. 论文中的举例:
总结
前言
最近在看一篇关于模板匹配的论文,里面的使用模板匹配的算法是改进版的NCC,即Fast NCC,看网上没有关于Fast NCC的解说,就想着记录一下自己学习的过程,写一下自己对这个改进算法的解释,论文的全称是《Template Matching using Fast Normalized Cross Correlation》,有感兴趣的可以自己去了解一下。(因为有的内容不好打字,下面我会用手写图片)
一、基础知识
从最简单的初高中知识开始:均值、标准差、方差、协方差、相关系数


二、NCC基本公式以及解决问题
1. NCC基本公式
本文讨论的问题是确定给定模式在二维图像中的位置。设 f(x,y) 表示图像在点 (x,y) 处的强度值,图像大小为 Mx × My,其中 x∈{0,…,Mx -1},y∈{0,…,My -1}。模式由给定的模板 t 表示,模板大小为 Nx × Ny。计算模板匹配程度高低就是在点 (x,y) 处计算归一化互相关值,即NCC系数,系数值越高说明越匹配,有系数基本公式:与 “一、基础知识” 中的相关系数 r 同理
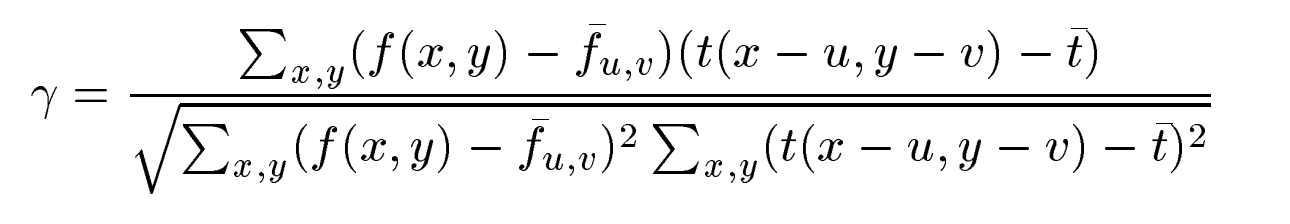
如果图像越匹配,则图像和模板越趋向于线性关系(一次函数):
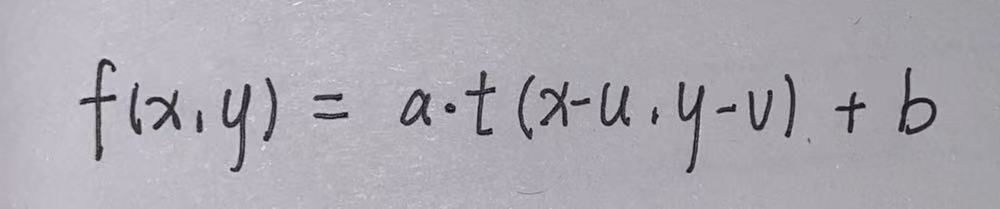
其中
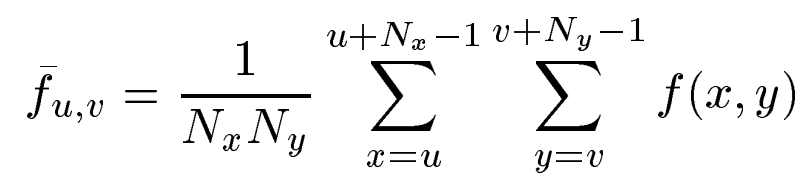
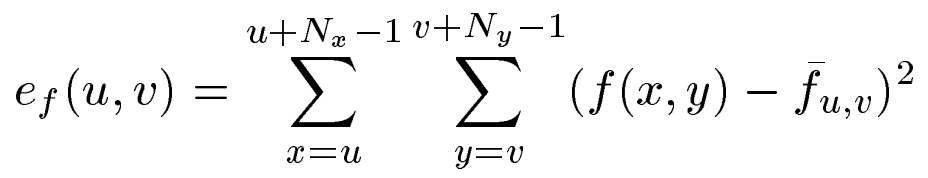
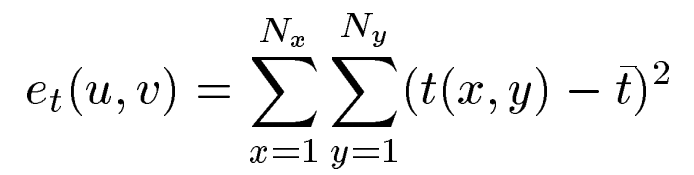
2. 基本公式解读

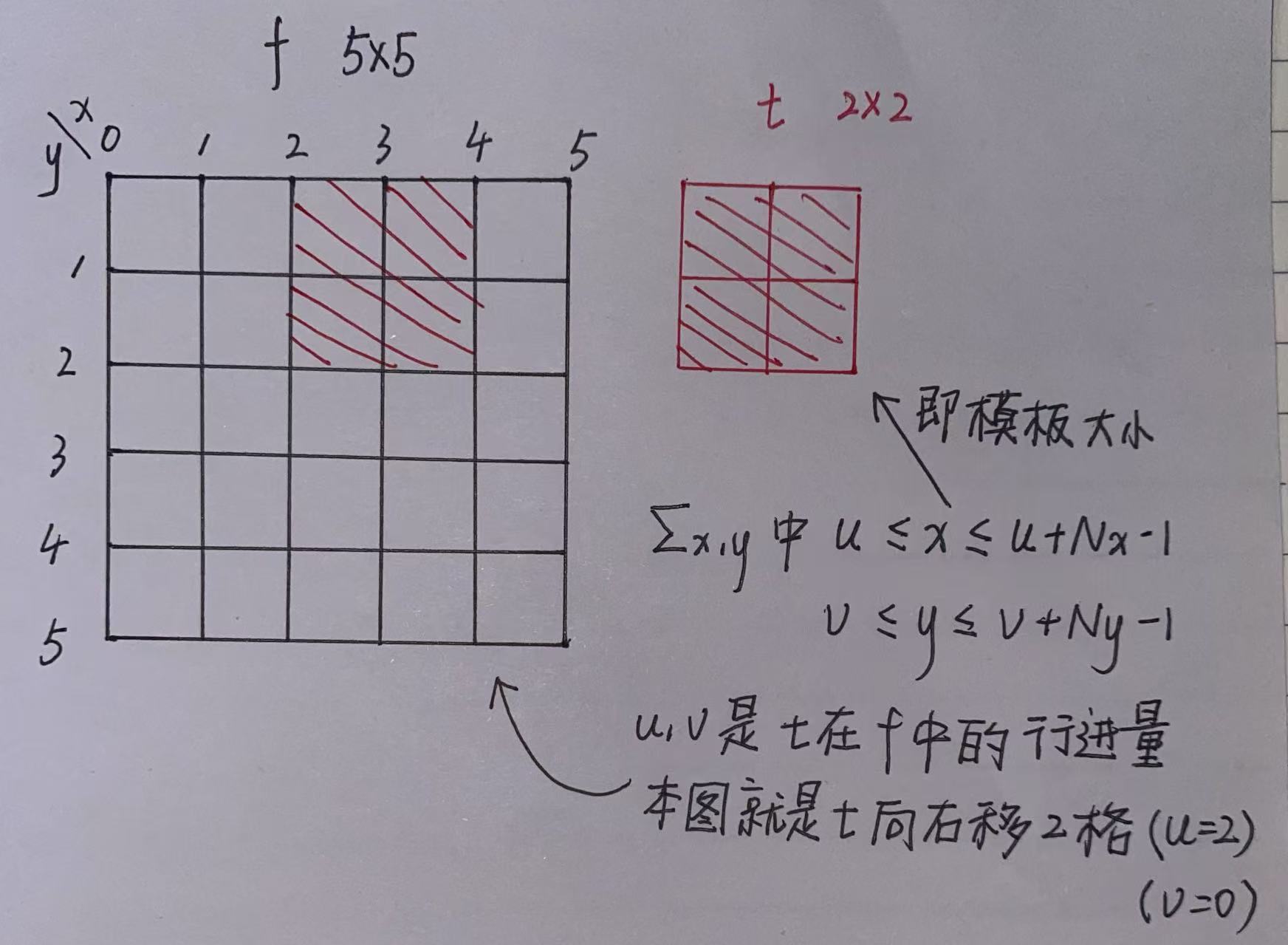
三、简化分母 fuv
1. 要简化的分母
由上面我们可知:
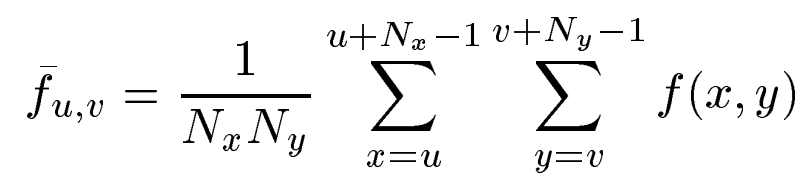
即模板所在图像位置,那一块模板区域图像的均值,我们可以知道,移动一次模板就需要计算一次模板所在区域图像的均值,计算时间需要很久,于是就提出了用积分表快速计算 fuv。(因为模板部分方差容易计算就先不管,这里主要是简化计算图像部分的方差)
2. 积分图
(作图有点粗糙看得懂就行)

即
![]()
![]()
推广到区域积分:
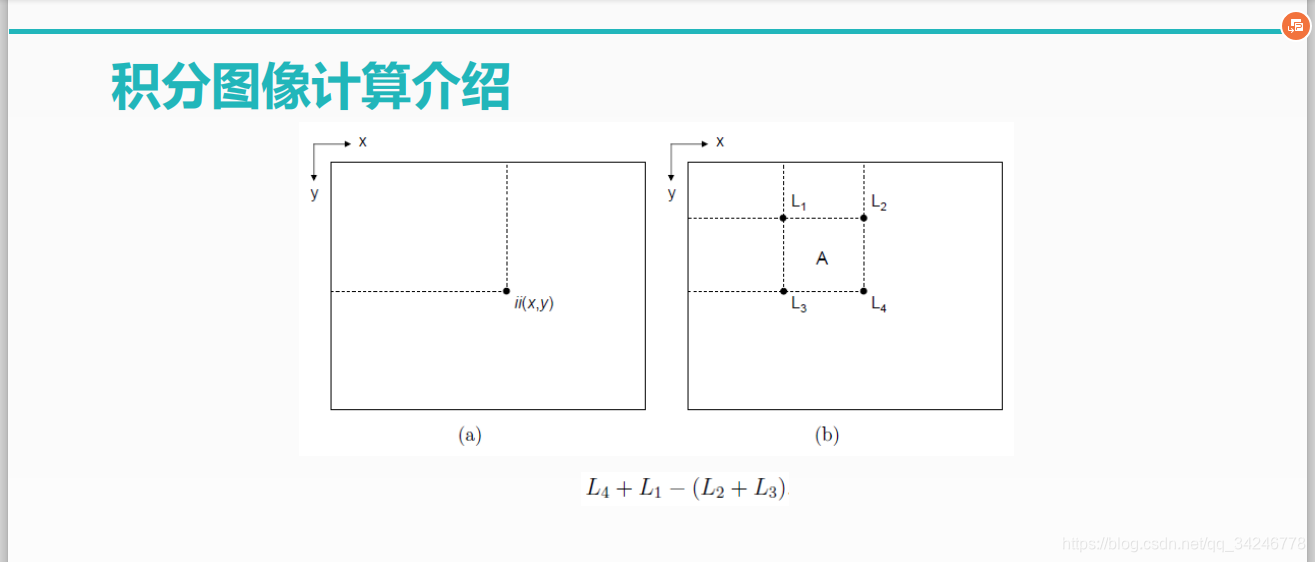
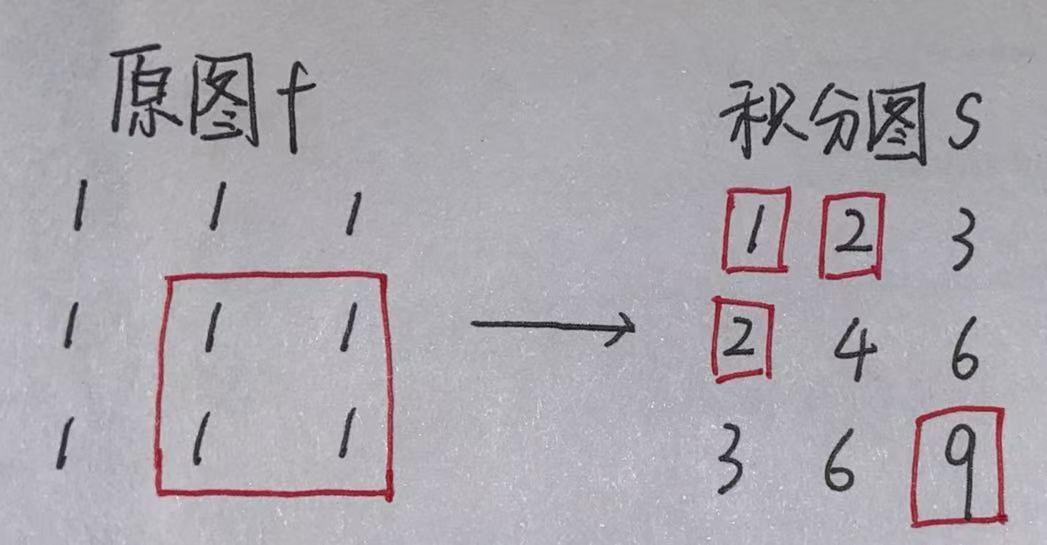
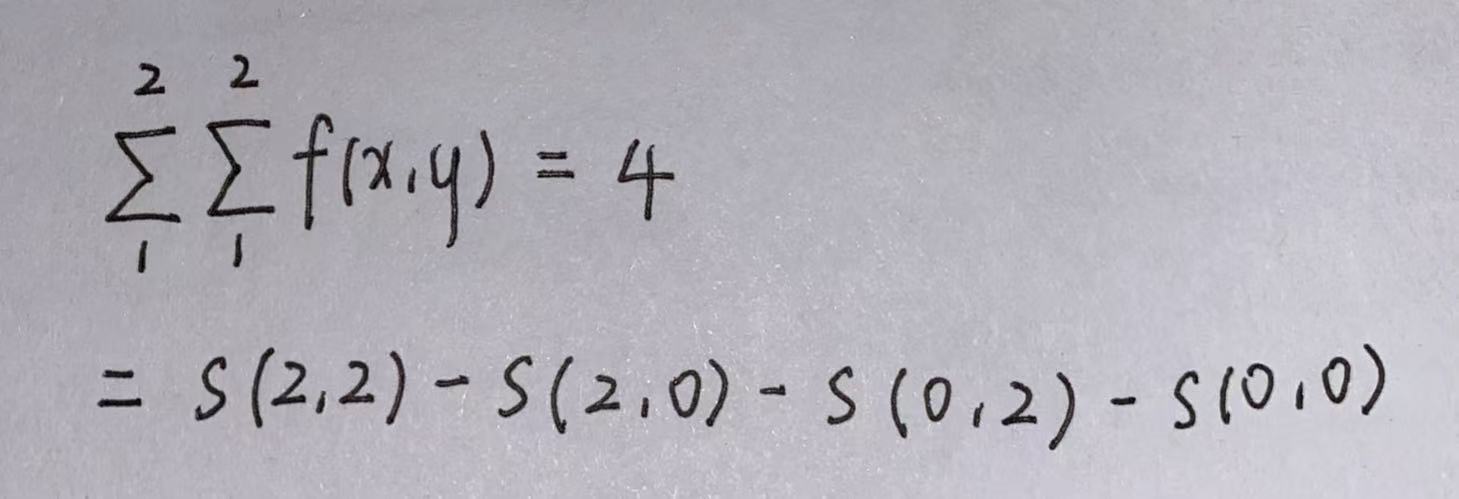
就有了以下公式,只需要三次相加减就可以算出模板区域内的图像强度均值:
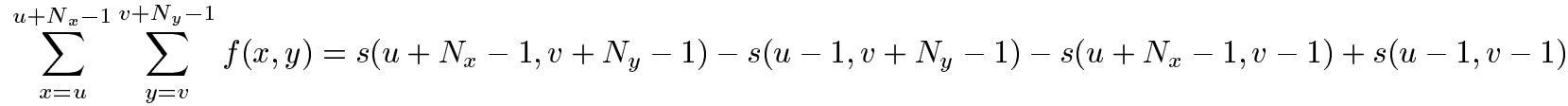
3. 分母拆开化简
NCC的分母可以拆开变成:
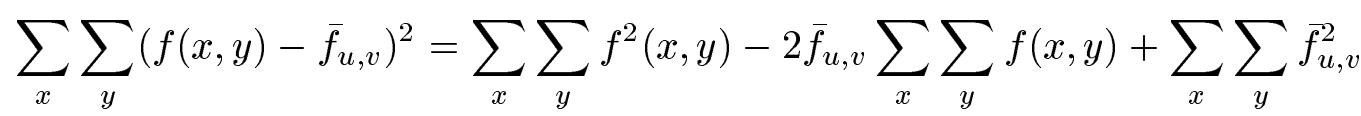
其中:
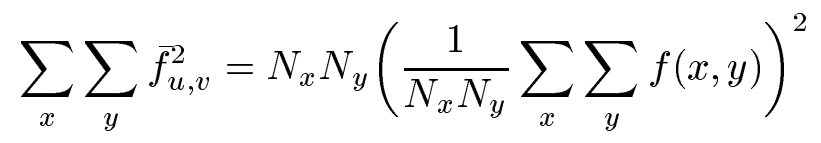
解释一下其中的参数:

但是不要忘记还有:
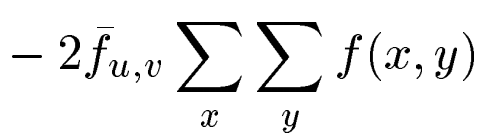
化简一下:
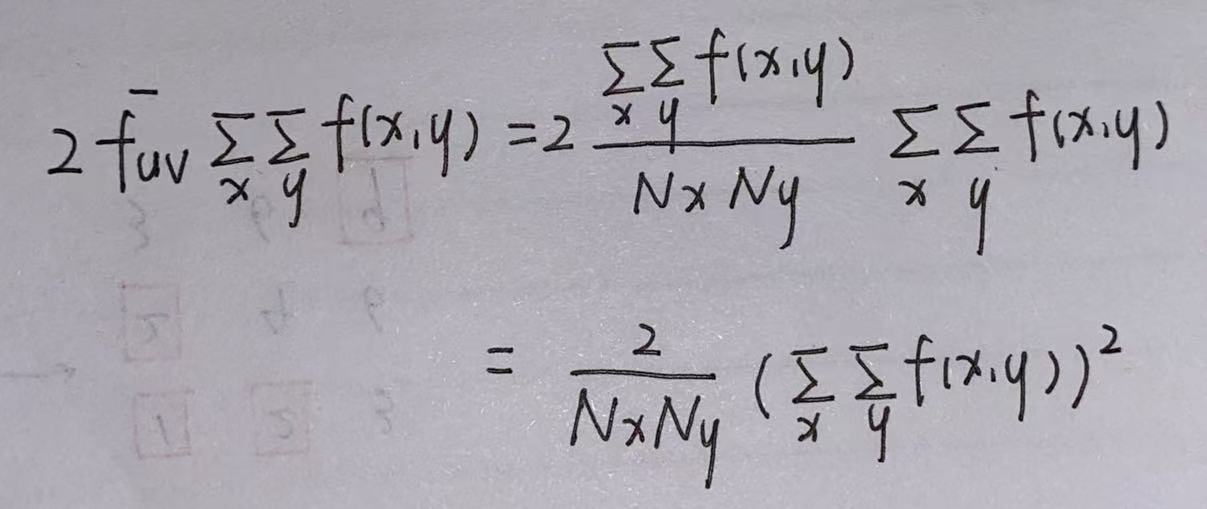
最后可得:
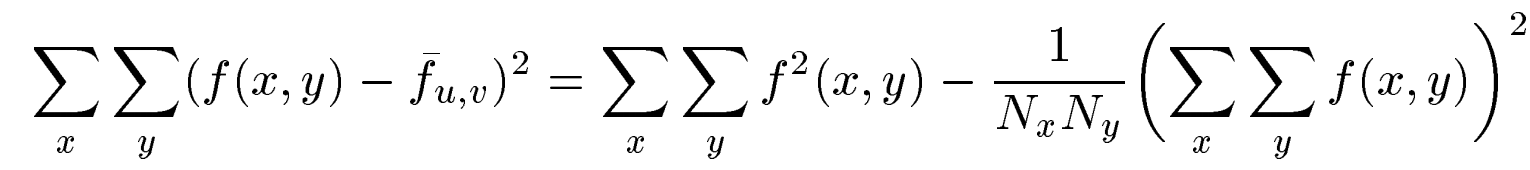
分母简化完毕!!!只靠积分表就实现了计算
四、简化分子
1. 要简化的分子
分子原式:
![]()
可以写成分子N(u,v)
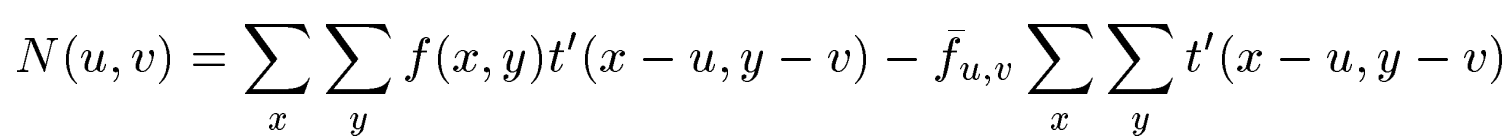
其中:t'(x-u,y-v) 为
![]()
由于 t′ 的均值为零,因此其总和也为零,故有:
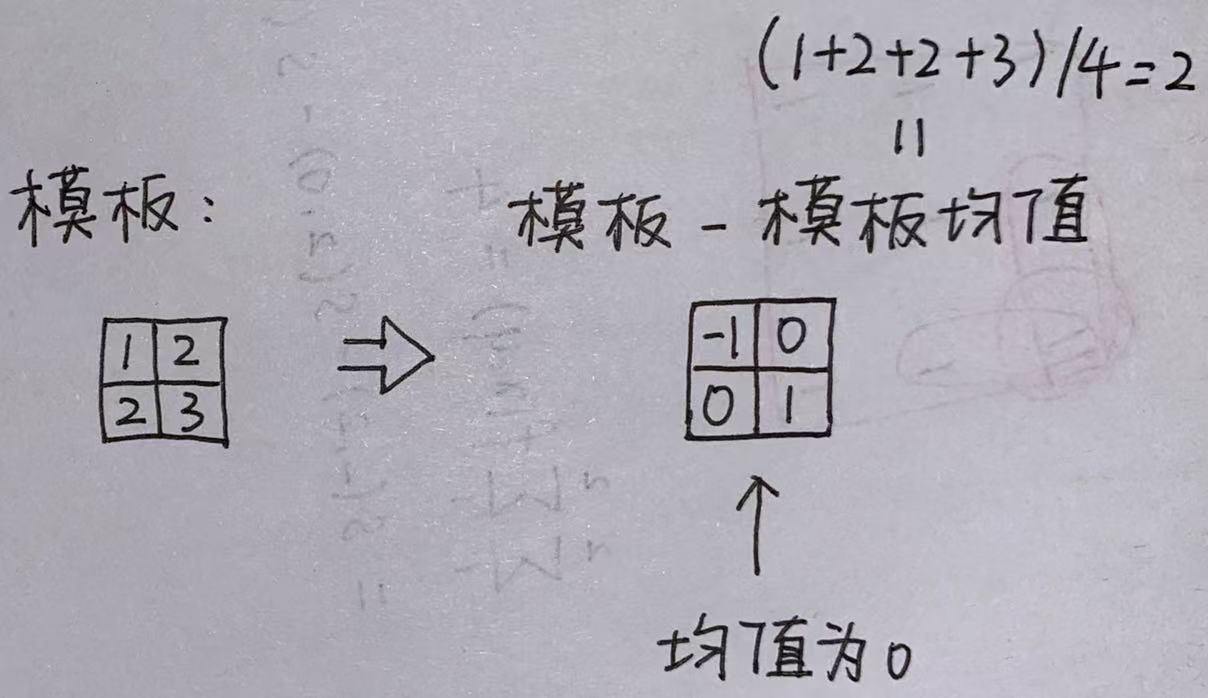
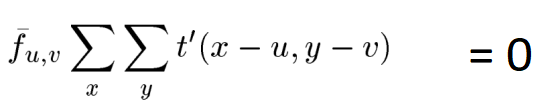
所以分子N(u,v)只剩下:
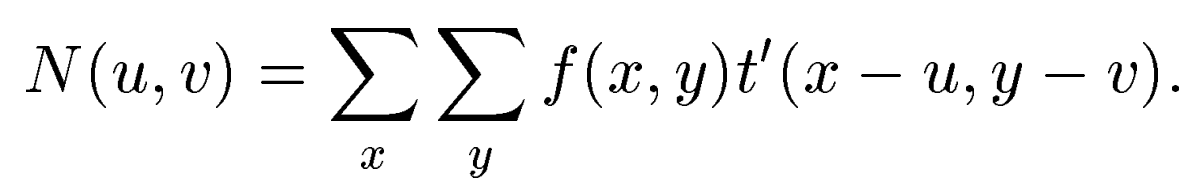
2. 模板函数的近似
将![]() 展开成K个矩形基函数
展开成K个矩形基函数![]() 的加权和,得到近似值
的加权和,得到近似值![]() ,详细为:
,详细为:
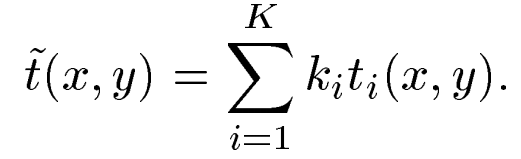
![]() 为加权系数,
为加权系数,![]() 为基函数。
为基函数。
3. 基函数简单解释
基函数在这里可以暂且理解为在一些区域等于1,其他区域都为0,所以可以化简:

举个例子,下图就是在6 <= x <= 14 ^ 8 <= y <= 12区域为1,其他区域为0的基函数:
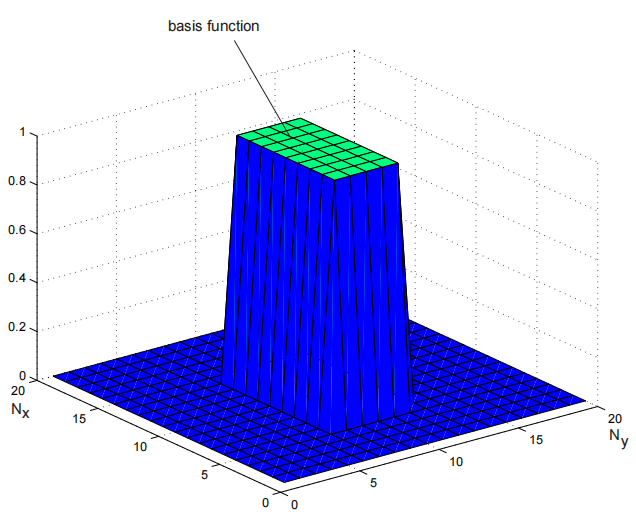
所以分子N(u,v)可以近似为:
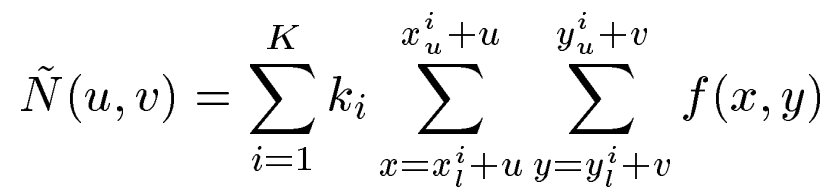
论文中写了确定基函数有两种方法,第一种是手动确定,第二种是自动确定。
与上面的分母同理,这里也可以运用积分表:
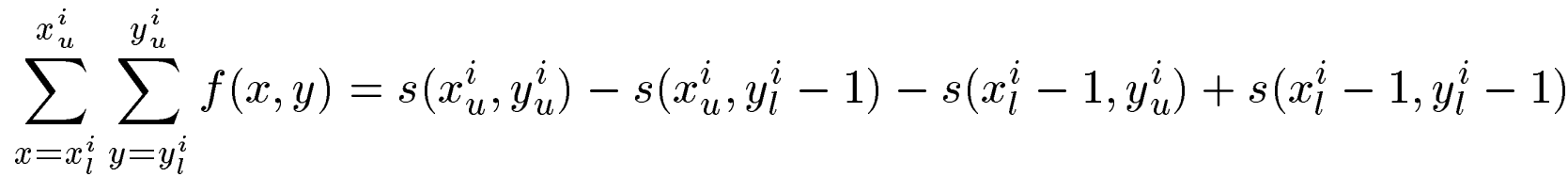
也成功化简了分子!!!只需要三次相加减就可以求得分子
五、Fast NCC归一化互相关值
1. 最终公式
简化完分子和分母之后,可以得到NCC归一化的近似值:
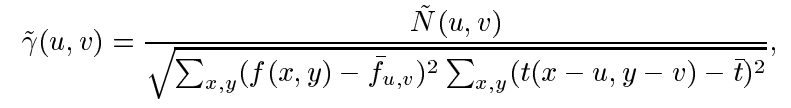
最终式子即为:
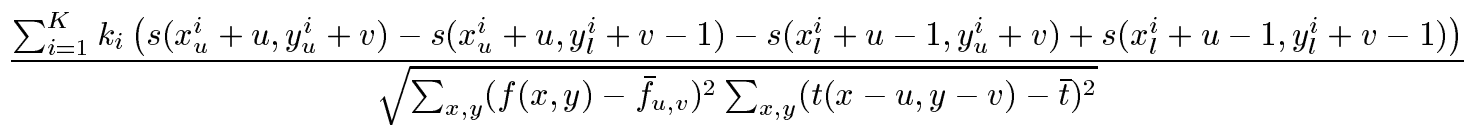
完成了NCC算法的加速。
2. 复杂性对比
复杂性分析:
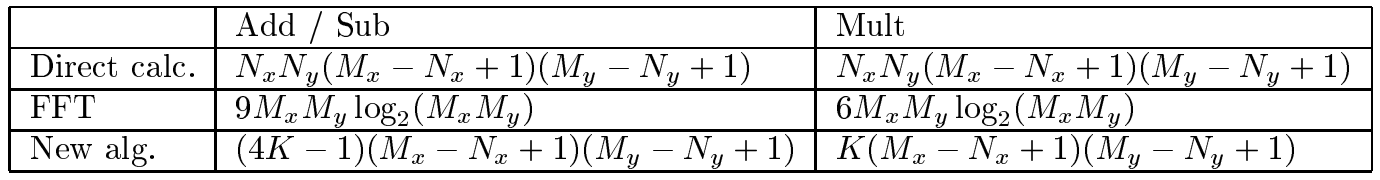
举例说明,可以得出Fast NCC的算法复杂性最低

3. 论文中的举例:

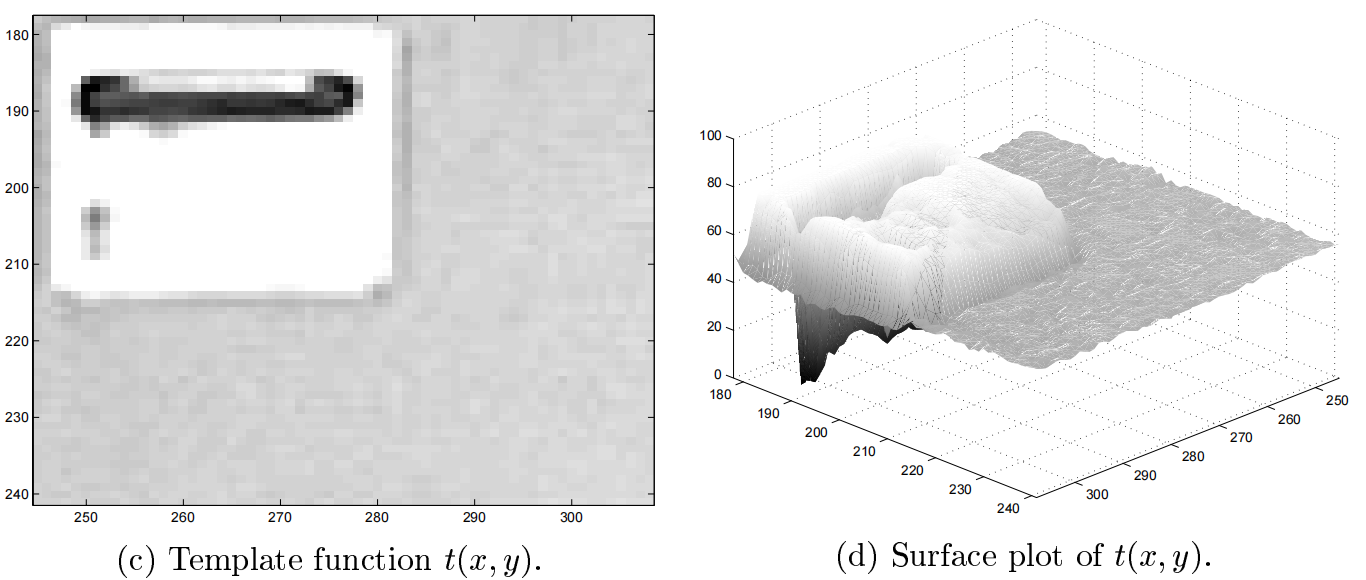
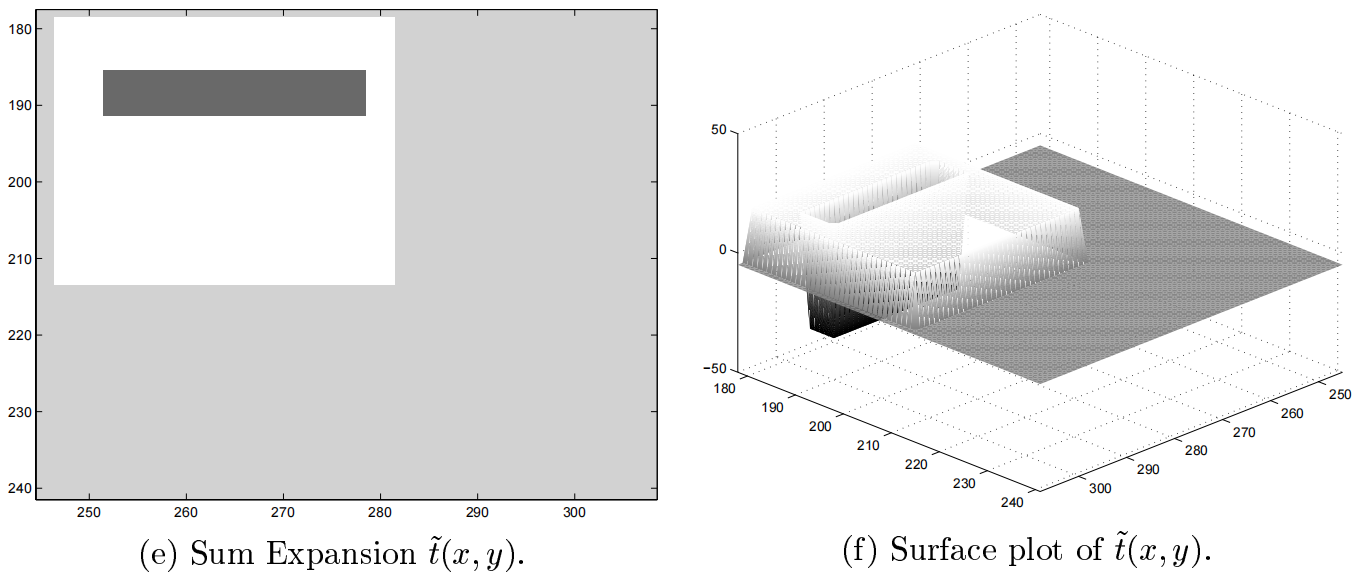
几个图的说明:
(a) 原始图像 (b) 经过Fast NCC算法的交叉相关矩阵(u,v)
(c) 原始模板图像 (d) 原始模板图像曲面图
(e) 基函数处理过后的模板图像 (f) 处理过后的模板图像曲面图
总结
这篇文章对Fast NCC进行了一个解读,介绍了如何简化分母和分子,并求得近似值进行加速计算,最后得到了最终Fast NCC的算法公式,其复杂度远低于直接计算以及FFT,但是其中的基函数还有待考究,后续学习会继续补充。





JavaScript 基础知识)
(二))












