外旋是固定坐标系，内旋是动态坐标系。外旋和内旋具有等价性。
固定坐标系依次绕xyz轴旋转，旋转矩阵
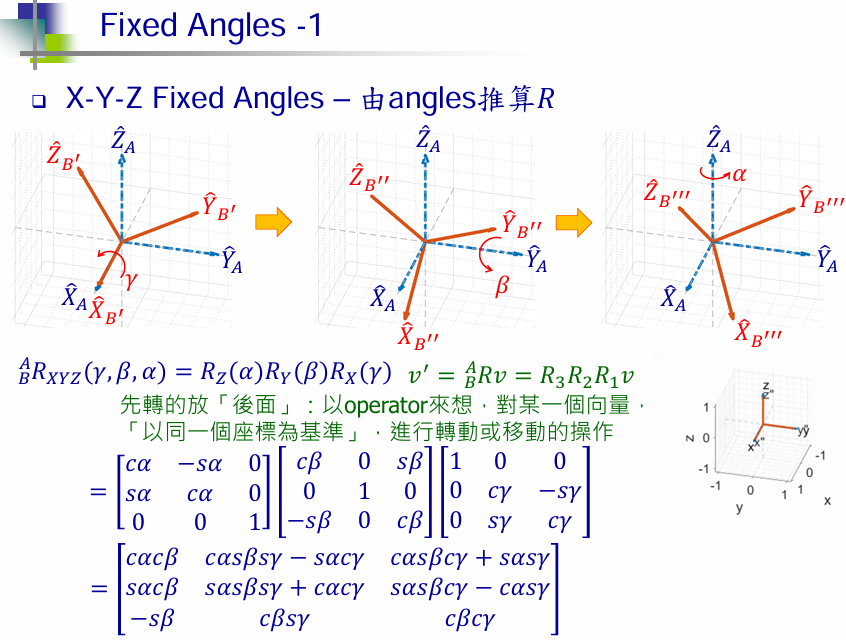
动态坐标系依次绕zyx轴旋转，旋转矩阵
numpy和scipy计算对比
import numpy as np
from numpy import sin, cos, pi # 抑制科学计数法，小数点后保留后4位
np.set_printoptions(precision=4, suppress=True)
def euler_to_rotation_matrix(roll=0, pitch=0, yaw=0):"""欧拉角转为旋转矩阵动态坐标系，内旋矩阵依次zyx旋转固定坐标系，外旋顺序依次是xyzroll, pitch, yaw,绕xyz轴旋转的弧度"""gamma, beta, alpha = roll , pitch, yawsin_gamma = sin(gamma)sin_beta = sin(beta)sin_alpha = sin(alpha)cos_gamma = cos(gamma)cos_beta = cos(beta)cos_alpha = cos(alpha)r11 = cos_alpha * cos_betar12 = cos_alpha * sin_beta * sin_gamma - sin_alpha * cos_gamma r13 = cos_alpha * sin_beta * cos_gamma + sin_alpha * sin_gammar21 = sin_alpha * cos_betar22 = sin_alpha * sin_beta * sin_gamma + cos_alpha * cos_gammar23 = sin_alpha * sin_beta * cos_gamma - cos_alpha * sin_gammar31 = -sin_betar32 = cos_beta * sin_gammar33 = cos_beta * cos_gammamatrix = np.array([[r11, r12, r13],[r21, r22, r23],[r31, r32, r33]])return matrixfrom scipy.spatial.transform import Rotation as R
def test1():roll = pi / 2pitch = 2 * pi / 3yaw = pi / 4print(f"roll: {roll}, pitch: {pitch}, yaw: {yaw}")print("-----------Custom method-------------")rmat = euler_to_rotation_matrix(roll, pitch, yaw)print(f"rmat: \n{rmat}")print("-----------scipy method1--------------")rot = R.from_euler('xyz', [roll, pitch, yaw], degrees=False) # xyz小写是外旋print(f"rot: \n{rot.as_matrix()}") print( np.allclose(rmat, rot.as_matrix(), atol=1e-4) )print("-----------scipy method2--------------")rot2 = R.from_euler('ZYX', [yaw, pitch, roll], degrees=False) # ZYX大写是内旋print(f"rot2: \n{rot2.as_matrix()}")print( np.allclose(rmat, rot2.as_matrix(), atol=1e-4) ) # Truetest1()roll: 1.5707963267948966, pitch: 2.0943951023931953, yaw: 0.7853981633974483
-----------Custom method-------------
rmat:
[[-0.3536 0.6124 0.7071][-0.3536 0.6124 -0.7071][-0.866 -0.5 -0. ]]
-----------scipy method1--------------
rot:
[[-0.3536 0.6124 0.7071][-0.3536 0.6124 -0.7071][-0.866 -0.5 -0. ]]
True
-----------scipy method2--------------
rot2:
[[-0.3536 0.6124 0.7071][-0.3536 0.6124 -0.7071][-0.866 -0.5 -0. ]]
True
)
