线性代数

 外积与矩阵乘法的等价性

欧拉角的奇异性--万向死锁

现象

第二个轴旋转度，会导致第三个旋转轴和恶原始坐标轴的第一个旋转轴重合，导致第一次旋转与第三次旋转都使用了同一个轴进行旋转，也就是本质上旋转三次，但是只在两个自由度上旋转。

eg:

如下图，第二次的绕Y转90度之后，X就变到了初始坐标系下的Z轴方向上，第三次的绕X轴旋转，本质上还是绕空间中的这个坐标系的初始坐标的Z轴的自由度旋转。丢失了一个自由度。

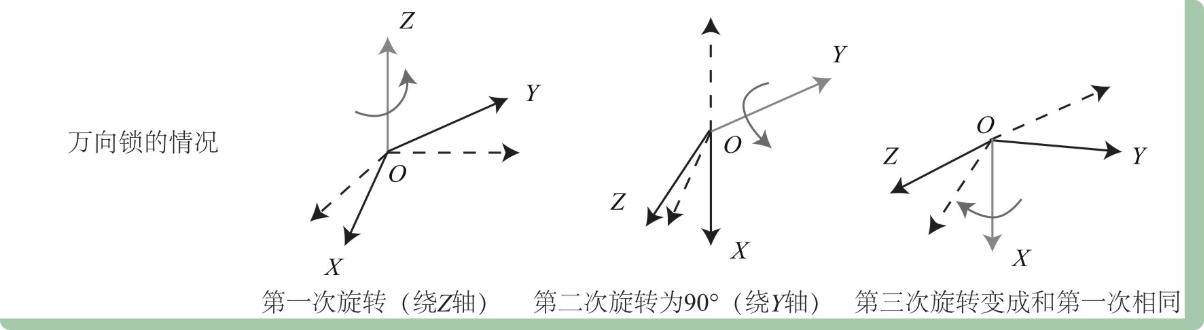
丢失一个自由度会导致什么问题

(1)旋转耦合

自由度丢失，导致第三次旋转的效果丢失，在最终的旋转矩阵中没有表现出来，也导致旋转矩阵中第一次旋转和第二次旋转的旋转角耦合，无法分离出角度。

(2) 控制指令冲突

• 如果系统试图调整航向（ψ），实际会影响横滚（ϕ），反之亦然。

• 示例（无人机）：

  • 飞控发送“增加航向角”指令，但实际可能同时改变横滚角，导致机体失控

解决方案

(1) 使用四元数（Quaternion）

• 优势：四元数通过4D空间描述旋转，无奇异性问题，适合连续旋转和插值（如球面线性插值SLERP）。

• 转换方法：欧拉角可转换为四元数处理，但需注意归一化和插值路径。