一、准备说明

1、这里介绍使用华为手机助手、海外代理软件结合固件将部分华为荣耀手机鸿蒙系统降级回EMUI系 统的一种方式；
2、需要降级的手机需要再出厂时内置系统为EMUI，出厂时为鸿蒙系统的无法进行降级操作；
3、降级有风险，存在刷机失败的情况，需自己斟酌。

二、操作步骤

1、首先下载海外代理软件 HiSuite Proxy这里使用的版本是HiSuite Proxy v3.3.0（博文使用荣耀V9进行的演示）

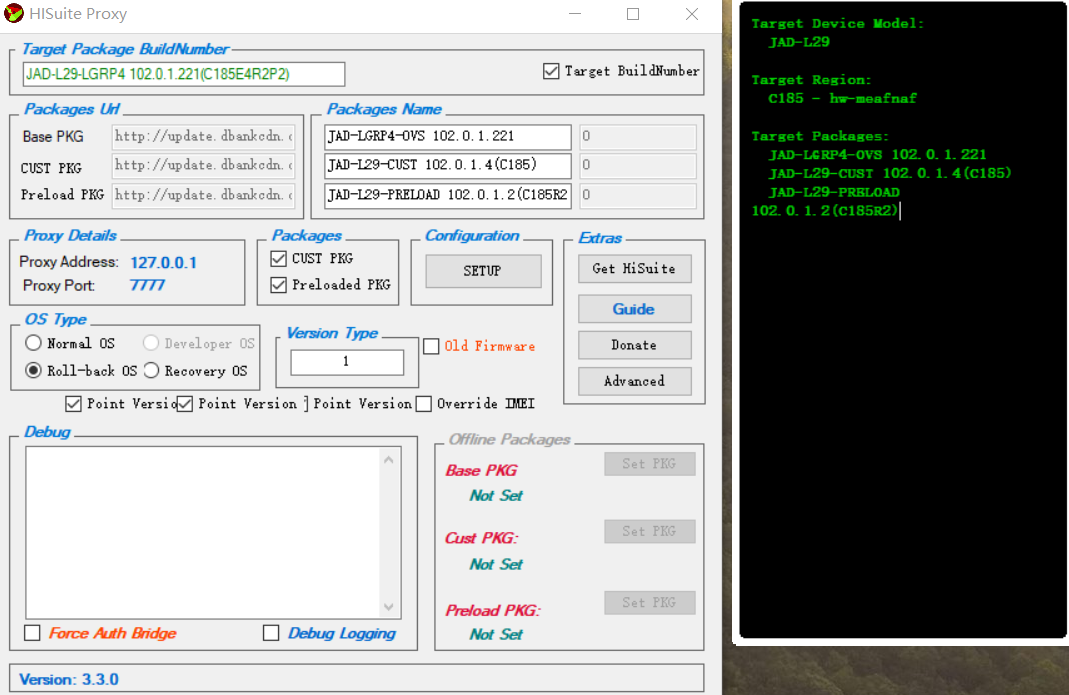
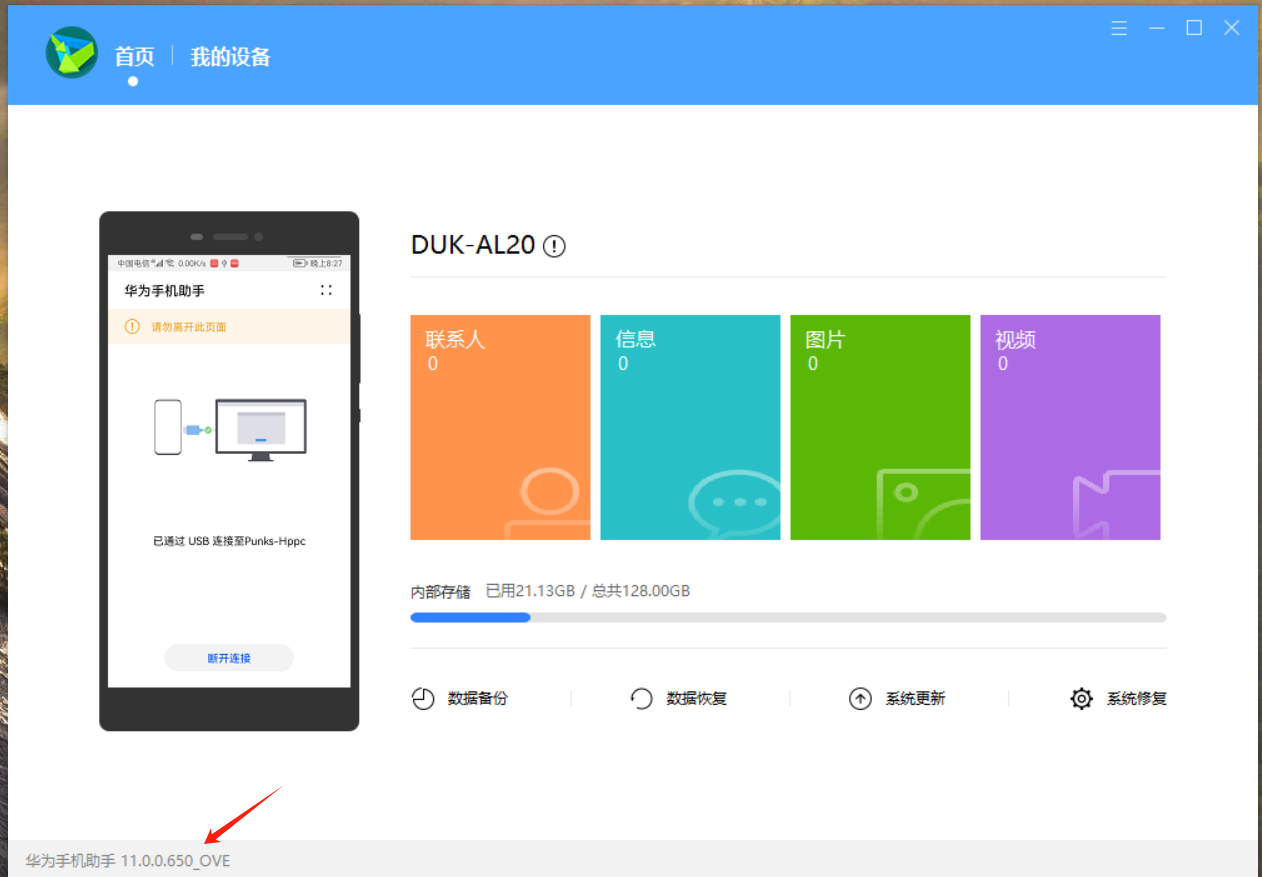
2、点击Get HiSuite自动跳转浏览器下载华为手机助手安装包，版本号为11.0.0.650_OVE
将手机与电脑连接，打开手机的设置-系统，记住手机的型号然后多次点击版本号，进入开发者模式，并允许进行usb调试。这里需要注意如果此时鸿蒙系统不是2.0需要先降回到2.0，才能进一步进行降到EMUI的操作。

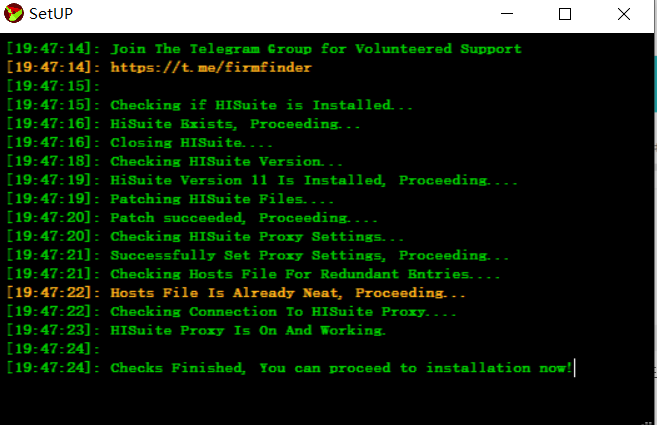
3、点击代理软件界面SETUP按钮，等待Checks Finished完成，华为手机助手会自动关闭

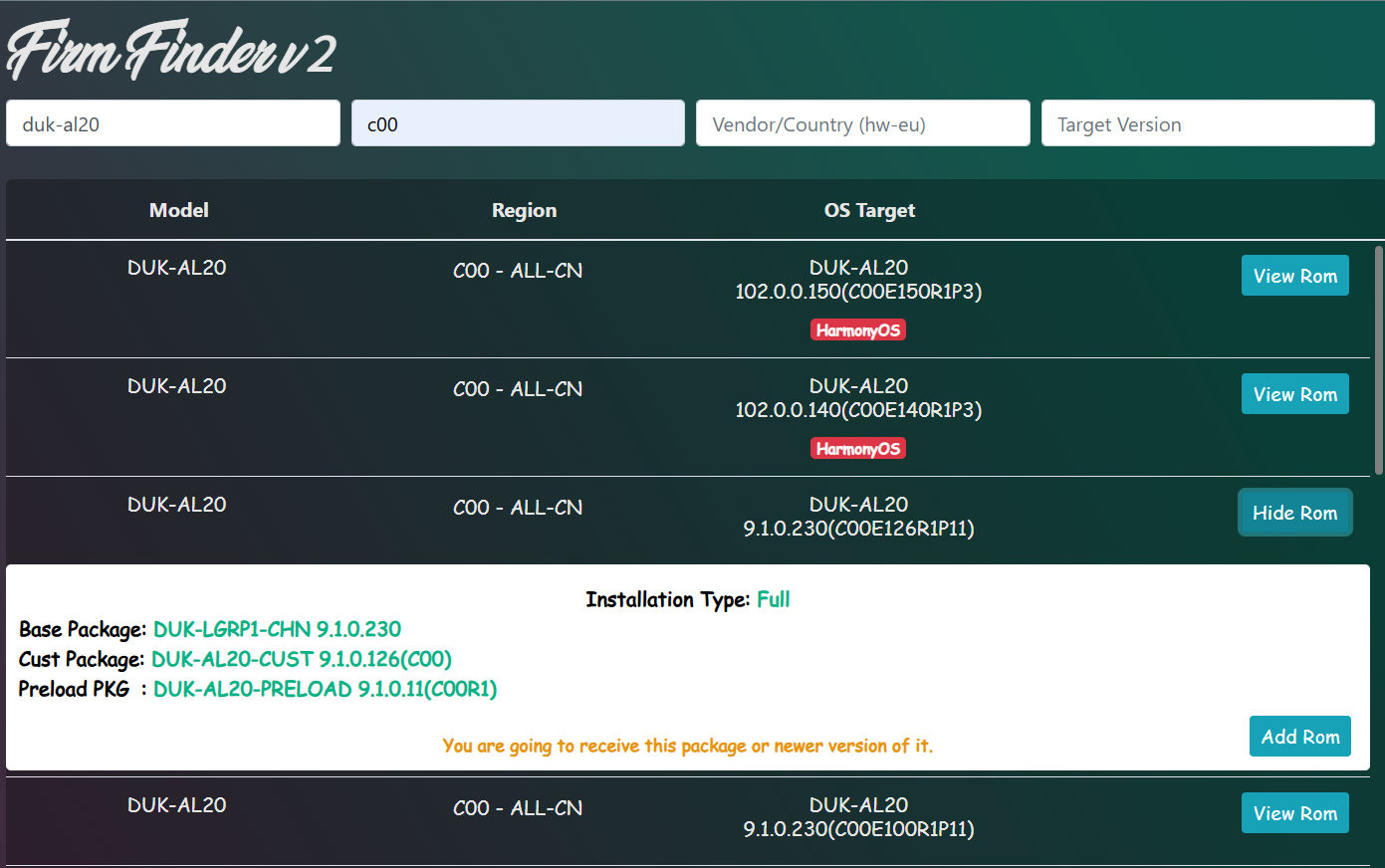
4、选择对应的固件，这里需要注意第一个是手机型号，第二个是地区，一般建议选择手机升级鸿蒙系统前的最后一个EMUI版本，其他版本可能会存在丢快充和USB的情况；选择适合的版本的点击Add Rom成功会在左下角提示Success
https://professorjtj.github.io/v2/

5、重新刷新打开华为手机助手，点击系统更新，此时会提示回退版本，按照操作进行系统降级，这里需要注意初始版本鸿蒙如果高于2.0版本需要先使用14.0.0.320版本进行降回到鸿蒙2.0再进行上述降EMUI流程，纯个人经验分享，欢迎交流。