一.基本概念

队列用来存储逻辑关系为“一对一”的数据，是一种“特殊”的线性存储结构。

特点：

•先进先出：队列中元素的添加（入队enqueue）和移除（出队dequeue）遵循先进先出的原
则。
•端点：队列有两个主要的端点——队头（front）和队尾（rear）。队头是队列中最先入队
的元素所在的位置，而队尾则是最后入队的元素所在的位置。

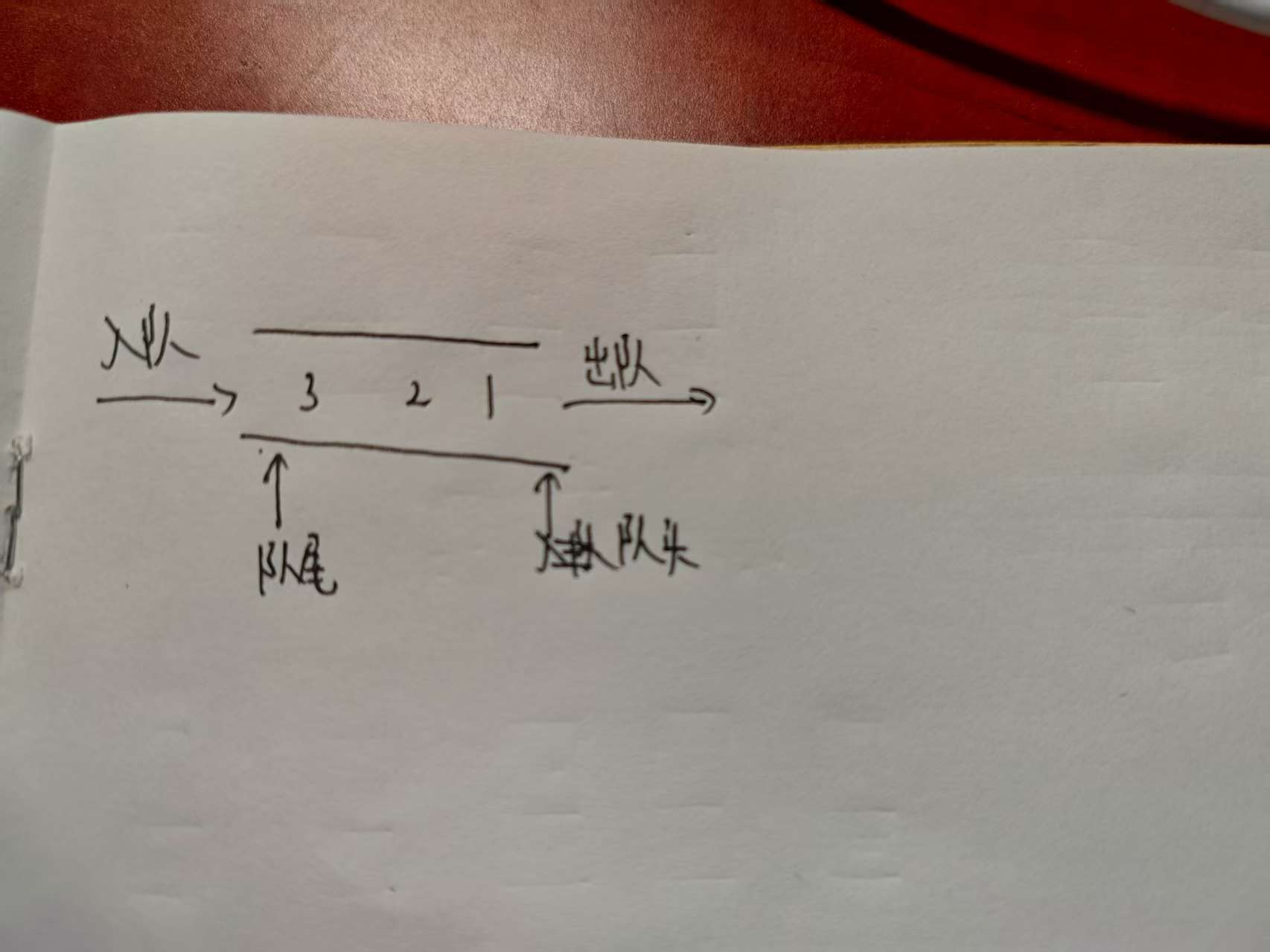
强调：栈和队列不要混淆，栈是一端开口、另一端封口，元素入栈和出栈遵循“先进后出”原则；队列是两端都开口，但元素只能从一端进，从另一端出，且进出队列遵循“先进先出”的原则。

        实现方法：

        1.顺序表实现

        2.链表实现

以链表的方式为例子

二.链表实现队列

        队列的API设计

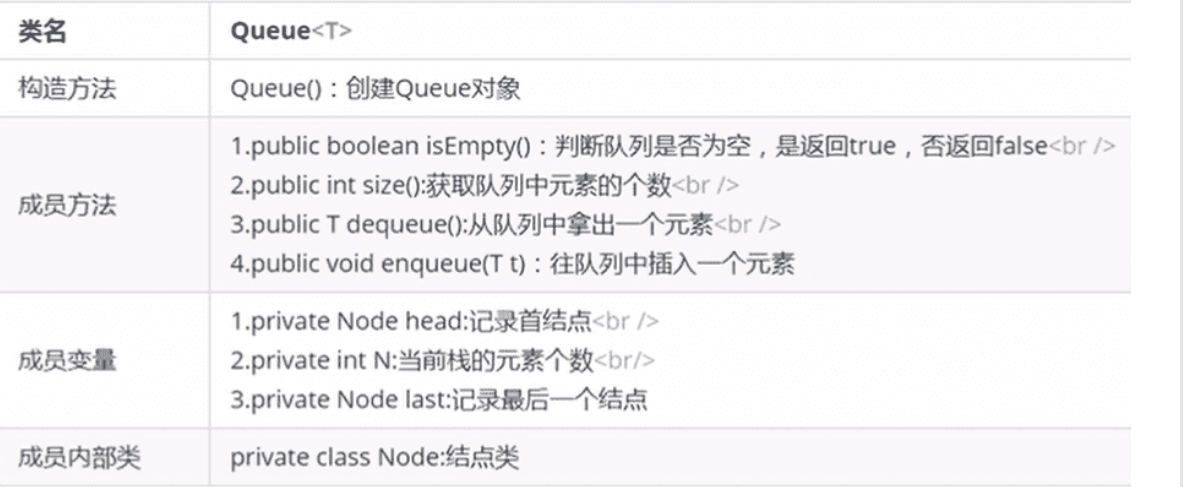
队列初始化

       

class Queue <T>
{//结点类class Node{public T data;//存储数据public Node next;//下一个结点public Node(T data , Node next){this.data = data;this.next = next;}}//创建首结点private Node head;//尾结点private Node last;//队列个数private int N;public Queue(){this.head =new Node(null,null);this.last =null;this.N =0;}

判断队列是否为空

思路分析：用布尔类型，直接返回数量

 //判断队列是否为空public boolean isEmpty(){return N == 0;}

获取队列个数

思路分析：直接返回数量

//返回队列元素个数public int size(){return N;}

插入元素

思路分析：

1.如果队列为空，将头结点指向新结点

2.创建变量1代替原先尾结点的数据

3.创建一个变量2当尾结点

4.将变量1的next引用指向变量2的值

 //插入元素public void enqueue(T data){//保存当前的尾结点Node oldLast = last;//创建新结点为新的尾结点last = new Node(data, null);//判断队列是否为空if(isEmpty()){head.next = last;}else{//将原先尾结点的next指向新结点oldLast.next = last;}N++;}

元素取出

思路分析：根据先进先出原则，我们需要更新头结点的next所指向的值

 //从队列拿出一个元素public T dequeue(){//为空，返回nullif(isEmpty()){return null;}//保存当前首结点Node oldFirst = head.next;//将首结点更新到下一个结点head.next = oldFirst.next;N--;//如果队列被删除完了，重置Last为nullif(isEmpty()){last = null;}return oldFirst.data;//返回取出元素}

三.用栈来实现队列

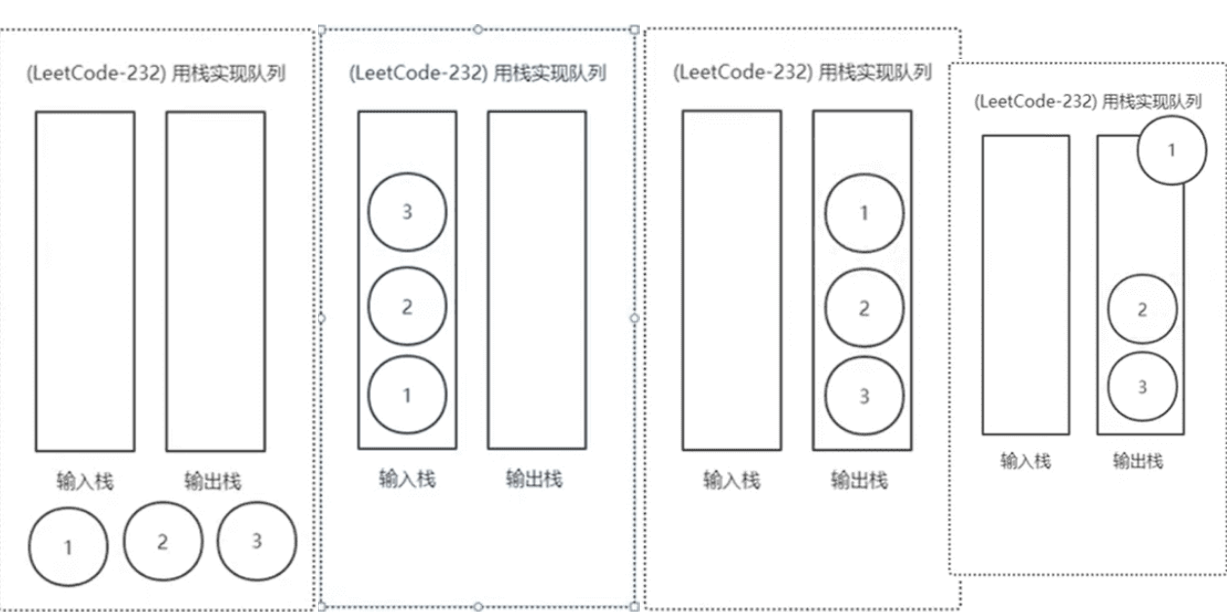
思路分析：

栈是后进先出（LIFO）的数据结构，队列是先进先出（FIFO）的数据结构。我们可以使用两个栈，一个用于入队操作（记为 inStack ），一个用于出队等操作（记为 outStack ）。 

当执行 push 操作时，直接将元素压入 inStack 。因为 inStack 只负责接收新元素，就像队列的尾部接收新元素一样。 

当执行 pop 和 peek 操作时，需要先判断 outStack 是否为空。如果 outStack 为空，就将 inStack 中的所有元素依次弹出并压入 outStack ，此时 outStack 栈顶元素就是队列的开头元素（因为 inStack 中先进入的元素会在转移到 outStack 后处于栈顶）。然后再执行相应的 pop 或 peek 操作。 

执行 empty 操作时，只需判断 inStack 和 outStack 是否都为空。  

完整代码

import java.util.Stack;class MyQueue {private Stack<Integer> inStack; // 用于入队操作的栈private Stack<Integer> outStack; // 用于出队等操作的栈public MyQueue() {inStack = new Stack<>(); // 初始化入队栈outStack = new Stack<>(); // 初始化出队栈}public void push(int x) {inStack.push(x); // 将元素x压入入队栈，模拟队列的入队操作}public int pop() {if (outStack.isEmpty()) { // 如果出队栈为空while (!inStack.isEmpty()) { // 当入队栈不为空时outStack.push(inStack.pop()); // 将入队栈的元素依次弹出并压入出队栈}}return outStack.pop(); // 弹出并返回出队栈的栈顶元素，即队列开头的元素}public int peek() {if (outStack.isEmpty()) { // 如果出队栈为空while (!inStack.isEmpty()) { // 当入队栈不为空时outStack.push(inStack.pop()); // 将入队栈的元素依次弹出并压入出队栈}}return outStack.peek(); // 返回出队栈的栈顶元素，即队列开头的元素（不弹出）}public boolean empty() {return inStack.isEmpty() && outStack.isEmpty(); // 判断入队栈和出队栈是否都为空，都为空则队列空}
}
public class StudentMS4
{public static void main(String[] args){MyQueue myQueue = new MyQueue();//调用pushmyQueue.push(1);myQueue.push(2);//调用peekSystem.out.println("队列开头的元素是："+myQueue.peek());//调用popSystem.out.println("移除并返回队列开头的元素："+myQueue.pop());//调用empty方法System.out.println("队列是否为空："+myQueue.empty());}
}

目录

一.基本概念

特点：

        实现方法：

二.链表实现队列

        队列的API设计

队列初始化

判断队列是否为空

获取队列个数

插入元素

元素取出

三.用栈来实现队列

思路分析：

完整代码

---