快速排序的基本思想：快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该基准值将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

1、递归版本

递归版本实现的主要框架：

void QuickSort(int* arr, int left, int right)
{if(left >= right){return;}int keyi = _QuickSort(arr, left, right);QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi+1, right);
} 

（1）hoare方法

这个函数的作用在于将基准值移到数组正确的位置并返回此处的下标。

left从基准值后一个位置开始移动，当left<=right时进入循环，left循环向前移动找比基准值大的数据，找到跳出循环，left循环向后移动找比基准值小的数据，找到跳出循环，此时若left<=right，交换left和right的数据，right--，left++继续循环。直到left>right跳出循环，此时right所在的位置就是基准值的正确位置，交换keyi和right的数据，返回right。

int _QuickSort(int* arr, int left, int right)
{int keyi = left;++left;while (left <= right){while (left <= right&&arr[left] < arr[keyi]){++left;}while (left <= right && arr[right] > arr[keyi]){--right;}if (left <= right){swap(&arr[right--], &arr[left++]);}}swap(&arr[keyi], &arr[right]); return right;}

上面代码有一处需要注意：

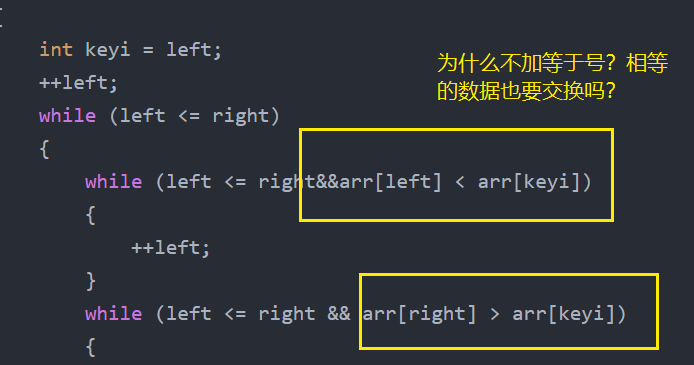
以下图为例：

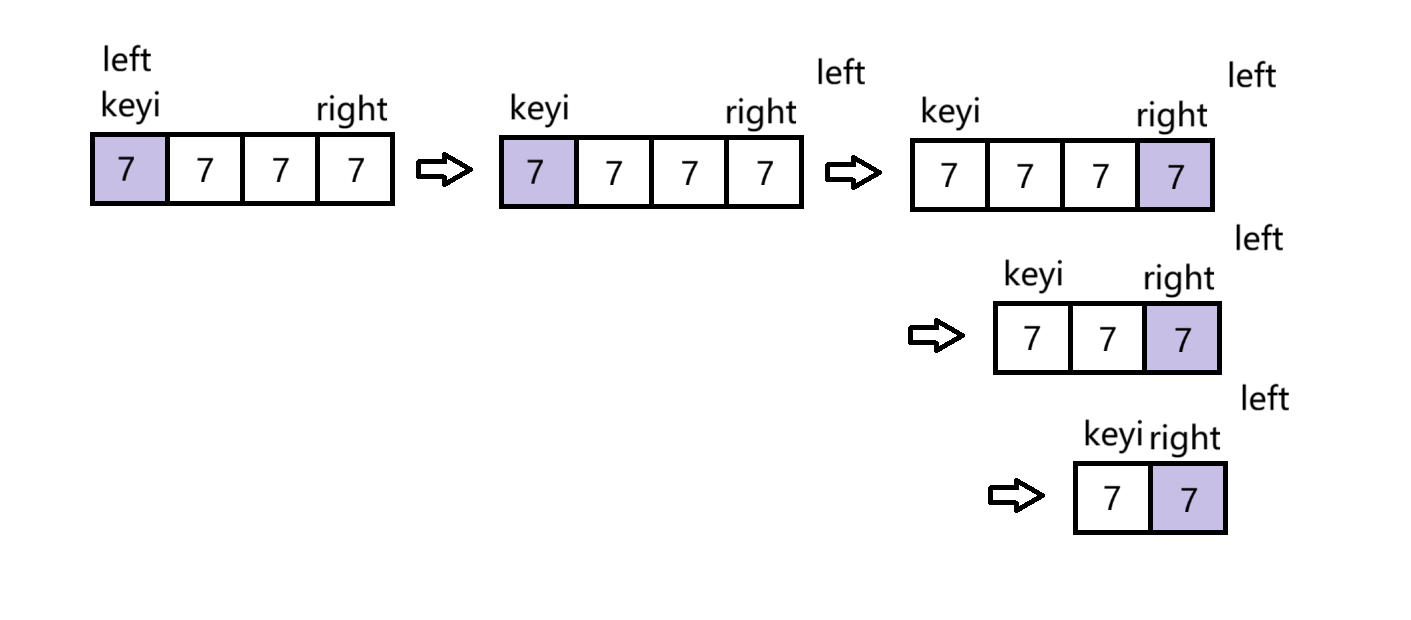
若存在数组中有很多个相同的值的情况，加等于号的代码会找到很多个相同的基准值，重复调用多次函数，而不加等于号的代码可以在一次函数调用中多次交换，避免无效的分割排序

（2）挖坑法

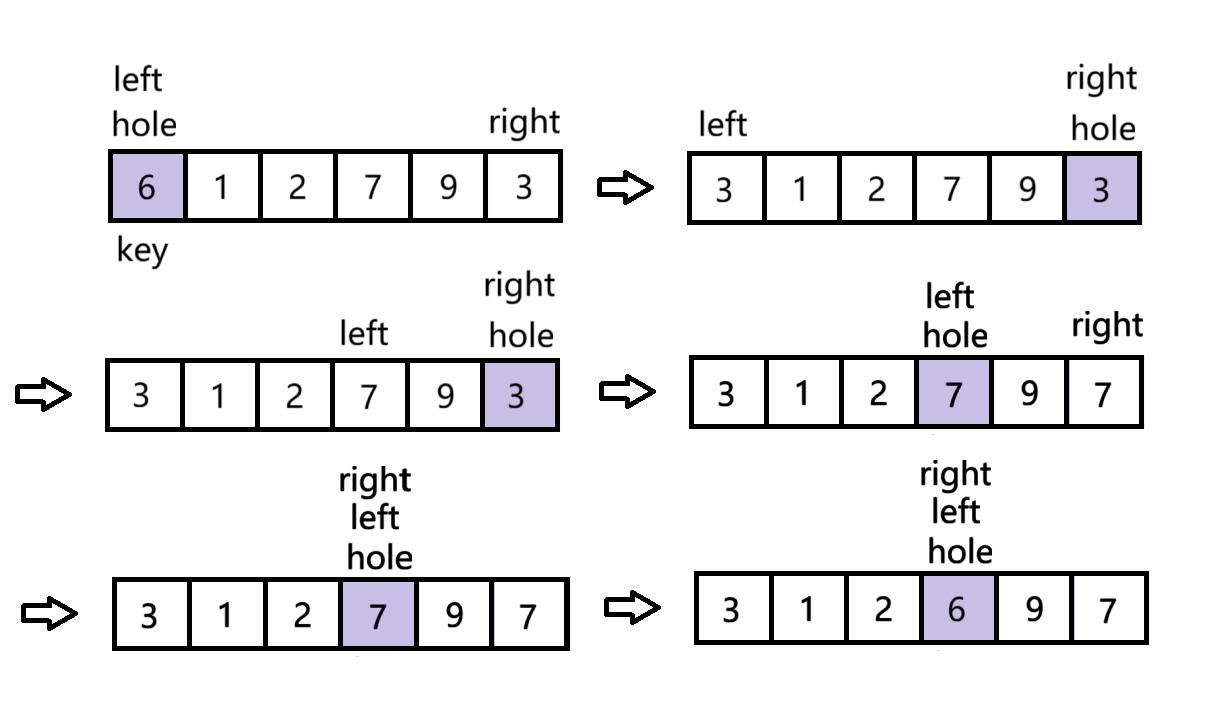
将left所在的位置看作坑，并设为基准值，将基准值用key保存下来，当left<right时进入循环，由于初始的坑在左侧，所以right先向后移动，找比基准值小的元素，找到后将right处的下标赋给hole，值也赋给hole，此时right所在的位置成为新的坑，再到left向后移动，找比基准值大的元素，找到后将left处的下标赋给hole，值也赋给hole，此时left所在的位置成为新的坑，继续循环。

跳出循环后，此时left和right和hole指向同一个位置，这个位置就是基准值的正确位置，将key赋给arr[hole],返回hole。

int _QuickSort1(int* arr, int left, int right)
{int hole = left;int key = arr[hole];while (left < right){while (left <right && arr[right] > arr[key]){--right;}arr[hole] = arr[right];hole = right;while (left <right && arr[left] < arr[key]){++left;}arr[hole] = arr[left];hole = left;}arr[hole] = key;return hole;
}

（3）lomuto前后指针

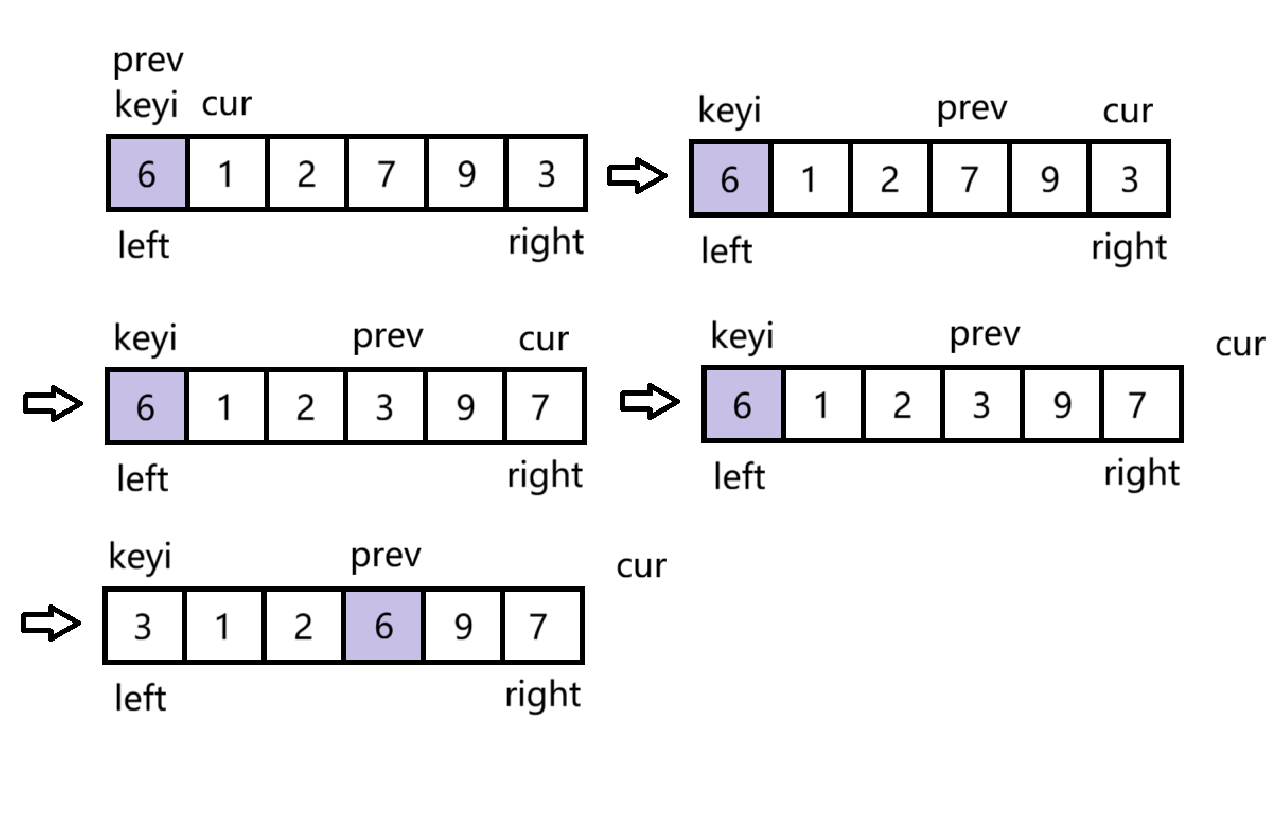
定义基准值为left所在的位置，把left赋给prev，cur为prev的后一个位置，当cur<=right时，进入循环，cur在前探路，找比基准值小的元素，若找到了则prev++，将prev和cur所在位置的元素对调，为了避免将同一个元素对调，可以将++prev加入到循环中，写成如下代码的形式。

跳出循环后，此时prev所在的位置就是基准值的正确位置，将arr[prev]和arr[keyi]对调，返回prev。

int _QuickSort2(int* arr, int left, int right)
{int keyi = left;int prev = left, cur = prev + 1;while (cur <= right){if (arr[keyi] > arr[cur] && ++prev != cur){swap(&arr[prev], &arr[cur]);}cur++;}swap(&arr[keyi], &arr[prev]);return prev;
}

2、非递归版本（用栈实现）

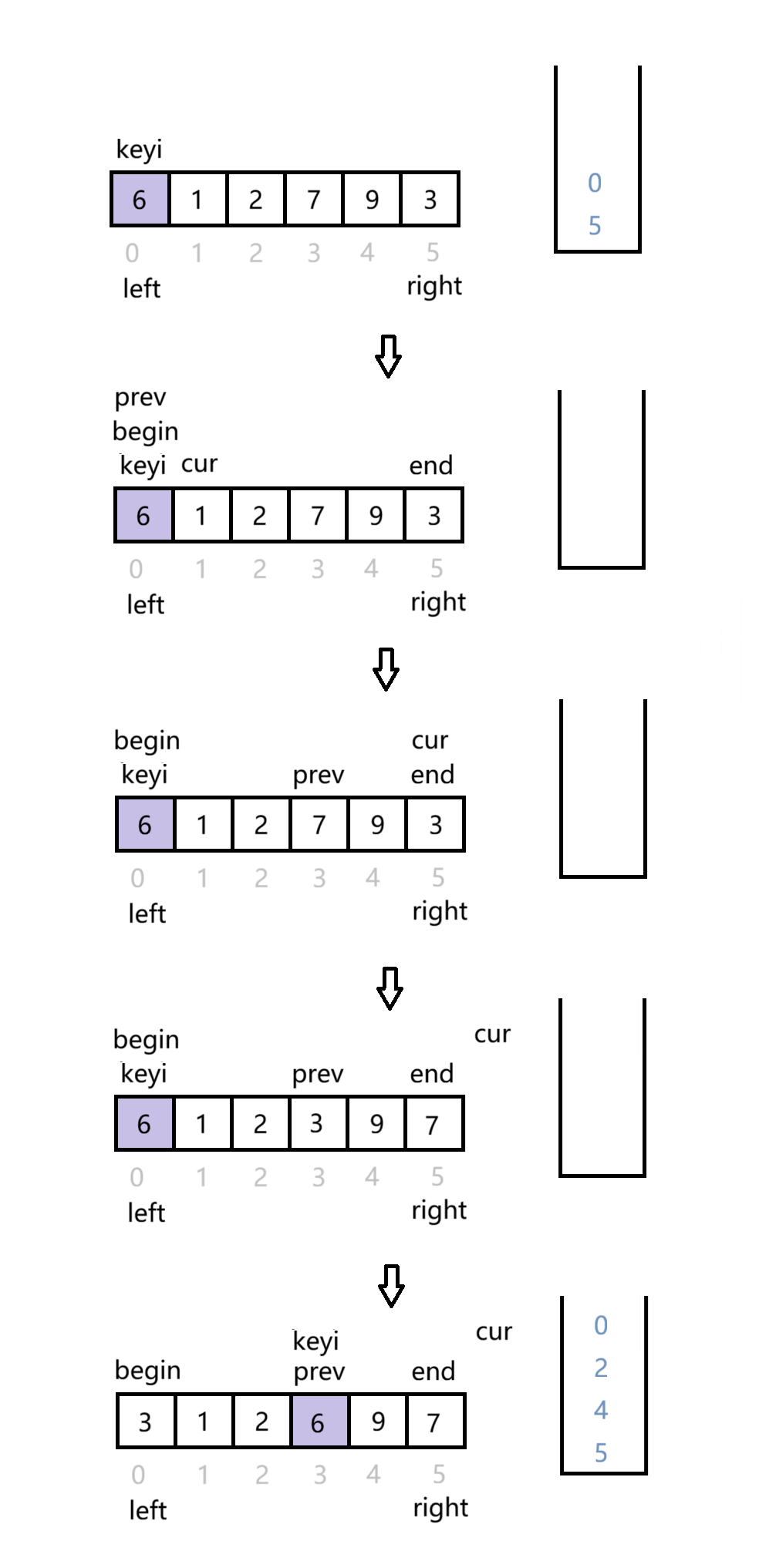
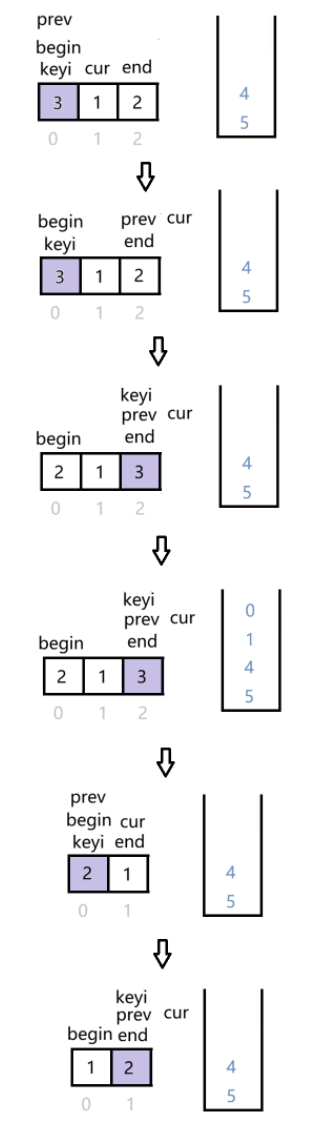
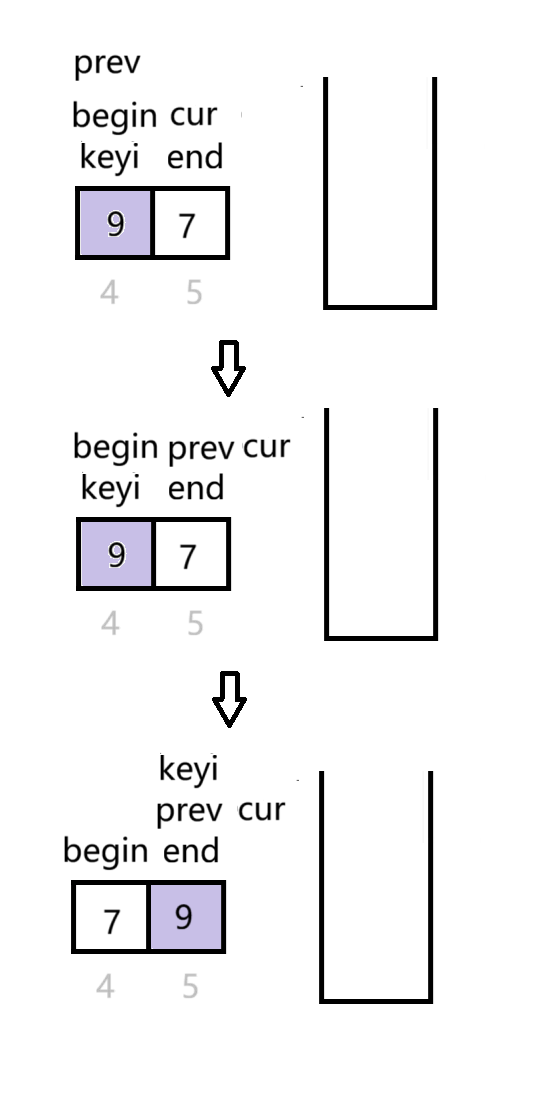
栈的作用在于保存需要排序的序列。先将数组头尾下标入栈，当栈不为空时进入循环，取两次栈顶元素分别赋给begin和end，取完后出栈，基准值为begin所在位置的元素，prev为begin所在位置cur为prev后一个元素的下标，prev与cur的作用与双指针法里的作用一样，找到基准值的正确位置后将prev赋给keyi，若keyi+1<end则将keyi和end作为新序列的头尾下标入栈，若begin<keyi-1则将begin和keyi-1作为新序列的头尾下标入栈，继续循环。

void QuickSortNonR(int* arr, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);int keyi = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (arr[keyi] > arr[cur] && ++prev != cur){swap(&arr[prev], &arr[cur]);}cur++;}swap(&arr[keyi], &arr[prev]);keyi = prev;if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi+1);}if (begin < keyi-1){STPush(&st, keyi-1);STPush(&st, begin);}}STDestroy(&st);
}

快速排序的时间复杂度为