注:本文为 “线性代数 | 行图像 / 列图像” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
MIT 线性代数笔记一 行图像和列图像
线性代数行图像与列图像解析
herosunly 已于 2022-01-25 15:34:26 修改
1. 学习背景回顾
若干年前,王清老师曾讲授线性代数课程。该课程授课音量较小,后排学生难以清晰聆听。根据模糊记忆,课程首讲内容为利用行列式求解方程组(即克莱姆法则),后续依次讲解矩阵的各类运算(包括加法、乘法、求逆与转置)、初等行变换,最终涉及特征值与特征向量的求解。整个学习过程以运算训练为主,却未阐明各类运算的本质意义。当时曾产生疑问:线性代数的核心是否仅为各类运算规则?但该疑问未得到进一步探究。
2. 当前学习规划
自 2018 年(大一时期)起,至今已过去十一年。2022 年新年的首要目标为系统学习李宏毅老师的《机器学习》。在学习“线性回归”章节时,为深化对理论知识的理解,需进行公式推导,此过程涉及矩阵求导公式的应用。为掌握该知识点,制定如下学习笔记。
3. 第一讲 行图像和列图像
3.1 线性方程组的矩阵表示
线性代数的核心问题之一是求解 nnn 元一次方程组。以二元一次方程组为例,其表达式如下:
{2x−y=0−x+2y=3\begin{cases} 2x - y = 0 \\ -x + 2y = 3 \end{cases} {2x−y=0−x+2y=3
将上述方程组用矩阵形式表示,可得:
[2−1−12][xy]=[03]\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} [2−1−12][xy]=[03]
其中,A=[2−1−12]\boldsymbol{A} = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}A=[2−1−12] 称为系数矩阵,x=[xy]\boldsymbol{x} = \begin{bmatrix} x \\ y \end{bmatrix}x=[xy] 称为未知数向量,等号右侧的向量记为 b\boldsymbol{b}b。由此,方程组可简化为矩阵方程:Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b。
3.2 行图像

行图像的几何意义与解析几何一致:在二维平面中,每个二元一次方程对应一条直线。绘制方程组中两个方程对应的直线,两条直线的交点坐标即为方程组的解。对于上述方程组,解得 x=1x = 1x=1,y=2y = 2y=2。
注:上图由 Wolfram Alpha 绘制生成:
- 2x-y = 0 and -x+2y=3 - Wolfram|Alpha
https://www.wolframalpha.com/input/?i=2x-y+%3D+0+and+-x%2B2y%3D3
3.3 列图像
3.3.1 列图像的核心思想
列图像分析的核心是将系数矩阵按列分解为若干列向量,此时求解原方程组等价于寻找列向量的线性组合,使其结果等于向量 b\boldsymbol{b}b。对于上述二元一次方程组,按列分解后可表示为:
x⋅[2−1]+y⋅[−12]=[03]x \cdot \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} x⋅[2−1]+y⋅[−12]=[03]
3.3.2 线性组合的定义
“向量的线性组合”是线性代数的核心概念之一,其运算包含两部分:
- 向量加法:需满足平行四边形法则或三角形法则;
- 向量数乘:对向量进行伸缩变换(系数大于 1 时向量伸展,系数大于 0 且小于 1 时向量收缩,系数小于 0 时向量反向并伸缩)。
特别地,若一组向量构成空间的“基向量”,则该空间内任意向量均可表示为这组基向量的线性组合。
3.3.3 列图像的几何意义
从几何角度看,列图像的求解目标是寻找系数 xxx 和 yyy,使得 xxx 与第一个列向量的数乘结果,与 yyy 与第二个列向量的数乘结果相加后,恰好等于向量 [03]\begin{bmatrix} 0 \\ 3 \end{bmatrix}[03]。
3.3.4 列图像的优势(以三元方程组为例)
对于二元方程组,行图像与列图像的优势差异不明显;但对于多元方程组,列图像的优势将显著体现。以三元一次方程组为例:
{x+2y+3z=62x+5y+2z=46x−3y+z=2\begin{cases} x + 2y + 3z = 6 \\ 2x + 5y + 2z = 4 \\ 6x - 3y + z = 2 \end{cases} ⎩⎨⎧x+2y+3z=62x+5y+2z=46x−3y+z=2
对于矩阵方程 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b:
- 若改变向量 b\boldsymbol{b}b 的数值,行图像中每个方程对应的平面均会发生变化,需重新分析平面间的位置关系;
- 列图像中,系数矩阵的列向量保持不变,仅需寻找新的线性组合系数即可,求解逻辑更简洁。
3.3.5 方程组有解的充要条件
- 核心问题:对于任意向量 b\boldsymbol{b}b,矩阵方程 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 是否均有解?(此处“任意”指所有可能的 b\boldsymbol{b}b)
- 列图像视角的转化:该问题等价于“系数矩阵的列向量的线性组合是否覆盖整个线性空间?”(选择线性空间作为研究对象,是因为 nnn 元一次方程组的解空间本质为线性空间)。
- 无解情况的反例:若系数矩阵的列向量线性相关(例如,第三个列向量恰好等于第一个列向量减去第二个列向量),则所有列向量将共面(二维平面);若向量 b\boldsymbol{b}b 不在该平面内,则列向量的任意线性组合均无法得到 b\boldsymbol{b}b,此时方程组无解。
- 奇异矩阵的定义:当列向量线性相关时,系数矩阵 A\boldsymbol{A}A 称为奇异阵(或不可逆矩阵)。在奇异阵条件下,并非所有 b\boldsymbol{b}b 都能使 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 有解。
- 一般结论:对于 nnn 维线性空间,若系数矩阵的 nnn 个列向量满足线性无关(即任意一个列向量均不能表示为其他列向量的线性组合),则对于任意 b\boldsymbol{b}b,方程组 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 均有解;若列向量线性相关,则其线性组合无法充满 nnn 维空间,方程组未必有解。
3.3.6 行图像与列图像的维度对比
从行图像视角分析三元方程组的解:
- 有唯一解:三个平面相交于一点;
- 无解:至少两个平面平行,或任意两个平面的交线互相平行;
- 无穷多解:三个平面相交于一条直线。
但当空间维度升高(如 n>3n > 3n>3)时,行图像无法直观绘制,交点位置更难以分析。而列图像通过“线性组合”的思想,将高维空间的解问题转化为向量组合问题,显著降低了分析复杂度。
3.4 总结
线性方程组可等价表示为矩阵方程 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b:
- 从“行视角”分析矩阵 A\boldsymbol{A}A,得到的是方程组中的每个独立方程,其几何意义为空间中的超平面;
- 从“列视角”分析矩阵 A\boldsymbol{A}A,得到的是系数矩阵的列向量,其核心是通过列向量的线性组合构造向量 b\boldsymbol{b}b。
矩阵作为融合两种视角且逻辑自洽的数学工具,是线性代数中的重要创举,为高维线性问题的分析提供了统一框架。
MIT—线性代数笔记 行图像和列图像
三少爷的键 编辑于 2018-10-10 13:33
1 行图像与列图像的基本概念(Row Picture & Column Picture)
1.1 线性方程的几何表示(The Geometry of Linear Equations)
线性代数的核心问题之一是求解 nnn 元一次线性方程组。以二元一次线性方程组为例,其标准形式如下:
{2x−y=0−x+2y=3\begin{cases} 2x - y = 0 \\ -x + 2y = 3 \end{cases} {2x−y=0−x+2y=3
将上述方程组表示为矩阵形式 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b,可得:
[2−1−12][xy]=[03]\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix} [2−1−12][xy]=[03]
其中各矩阵/向量的定义如下:
- 系数矩阵(Coefficient Matrix):A=[2−1−12]\boldsymbol{A} = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}A=[2−1−12],用于存储方程组中未知数的系数;
- 未知数向量(Unknown Vector):通常记为 x=[xy]\boldsymbol{x} = \begin{bmatrix} x \\ y \end{bmatrix}x=[xy],包含方程组中所有待求的未知量;
- 常数项向量(Constant Term Vector):记为 b=[03]\boldsymbol{b} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}b=[03],包含方程组等号右侧的常数项。
2 行图像(Row Picture)
2.1 行图像的几何意义
行图像基于解析几何的思想,将线性方程组中的每个方程对应为几何空间中的一条直线(二元情形)或一个平面(三元情形)。对于二元一次方程,通过以下步骤可确定其对应的直线:
- 求解方程的两组解(即满足方程的 (x,y)(x, y)(x,y) 坐标对);
- 在 x-yx\text{-}yx-y 平面上标记两组解对应的点;
- 连接两点形成的直线,即为该方程的行图像。
2.2 行图像的求解原理
线性方程组的解对应于所有方程行图像的交点。对于本节中的二元方程组:
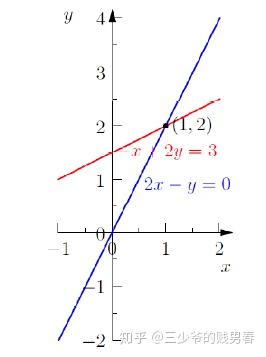
- 方程 2x−y=02x - y = 02x−y=0 的行图像为一条直线;
- 方程 −x+2y=3-x + 2y = 3−x+2y=3 的行图像为另一条直线;
- 两条直线的交点坐标 (x,y)=(1,2)(x, y) = (1, 2)(x,y)=(1,2),即为方程组的解。
3 列图像(Column Picture)
3.1 列图像的核心思想
列图像的本质是将系数矩阵 A\boldsymbol{A}A 按列分解为列向量,将方程组 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 转化为列向量的线性组合问题。对于本节中的二元方程组,系数矩阵的列向量分解形式如下:
x⋅[2−1]+y⋅[−12]=[03]x \cdot \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} x⋅[2−1]+y⋅[−12]=[03]
其中,xxx 和 yyy 是线性组合的系数(即方程组的未知数),目标是找到一组 x,yx, yx,y,使得列向量的线性组合结果等于常数项向量 b\boldsymbol{b}b。
3.2 线性组合的定义
对于给定的向量 c\boldsymbol{c}c、d\boldsymbol{d}d 及标量 xxx、yyy,表达式 xc+ydx\boldsymbol{c} + y\boldsymbol{d}xc+yd 称为向量 c\boldsymbol{c}c 与 d\boldsymbol{d}d 的一个线性组合。线性组合是线性代数中的核心概念,贯穿整个课程体系。
3.3 列图像的几何意义与求解
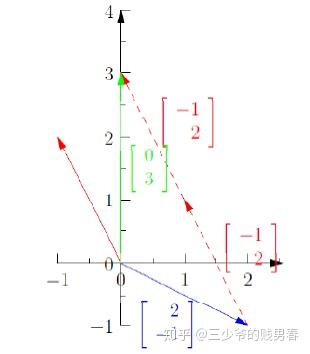
从几何角度看,列图像的求解过程是:找到标量 xxx、yyy,使得列向量分别乘以 xxx、yyy 后,通过“首尾相接”的向量加法得到 b\boldsymbol{b}b。对于本节的方程组:
- 蓝色向量为 [2−1]\begin{bmatrix} 2 \\ -1 \end{bmatrix}[2−1],乘以 x=1x = 1x=1 后得到 1⋅[2−1]=[2−1]1 \cdot \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 2 \\ -1 \end{bmatrix}1⋅[2−1]=[2−1];
- 红色向量为 [−12]\begin{bmatrix} -1 \\ 2 \end{bmatrix}[−12],乘以 y=2y = 2y=2 后得到 2⋅[−12]=[−24]2 \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} -2 \\ 4 \end{bmatrix}2⋅[−12]=[−24];
- 两向量相加:[2−1]+[−24]=[03]=b\begin{bmatrix} 2 \\ -1 \end{bmatrix} + \begin{bmatrix} -2 \\ 4 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} = \boldsymbol{b}[2−1]+[−24]=[03]=b,因此解得 x=1x = 1x=1,y=2y = 2y=2。
3.4 列向量线性组合的空间覆盖
若任意选取标量 xxx、yyy,则列向量 [2−1]\begin{bmatrix} 2 \\ -1 \end{bmatrix}[2−1] 与 [−12]\begin{bmatrix} -1 \\ 2 \end{bmatrix}[−12] 的所有线性组合将布满整个 x-yx\text{-}yx-y 平面。下图展示了该过程的几何直观:
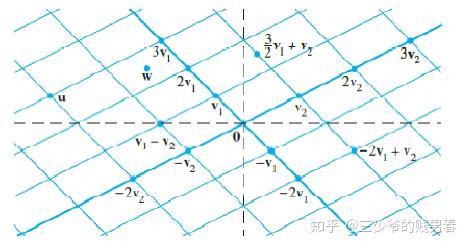
注:在 D.C.Lay 所著的《线性代数及其应用》中,曾绘制向量 v1=[−11]\boldsymbol{v}_1 = \begin{bmatrix} -1 \\ 1 \end{bmatrix}v1=[−11] 与 v2=[12]\boldsymbol{v}_2 = \begin{bmatrix} 1 \\ 2 \end{bmatrix}v2=[12] 的线性组合图像,其整数倍线性组合的端点在平面上形成网格,直观体现了线性组合对平面的覆盖。该书注重通过几何图像辅助理解线性代数概念,英文版已更新至第 5 版,中文版由华章出版社出版。
4 三元线性方程组的行图像与列图像
将上述二元情形的讨论扩展到三元情形,考虑如下三元一次线性方程组(选取 G. Strang 教材中的示例以匹配配图):
{x+2y+3z=62x+5y+2z=46x−3y+z=2\begin{cases} x + 2y + 3z = 6 \\ 2x + 5y + 2z = 4 \\ 6x - 3y + z = 2 \end{cases} ⎩⎨⎧x+2y+3z=62x+5y+2z=46x−3y+z=2
其矩阵形式为:
[1232526−31][xyz]=[642]\begin{bmatrix} 1 & 2 & 3 \\ 2 & 5 & 2 \\ 6 & -3 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 6 \\ 4 \\ 2 \end{bmatrix} 12625−3321xyz=642
4.1 三元方程组的行图像
三元一次方程的行图像为三维空间中的一个平面,方程组的解对应于三个平面的交点:
- 若三个平面相交于唯一一点,则方程组有唯一解;
- 若三个平面无公共交点(如存在平行平面、两两交线平行),则方程组无解;
- 若三个平面相交于一条直线,则方程组有无穷多解。
下图展示了该三元方程组行图像的几何直观(三个平面的相交关系):
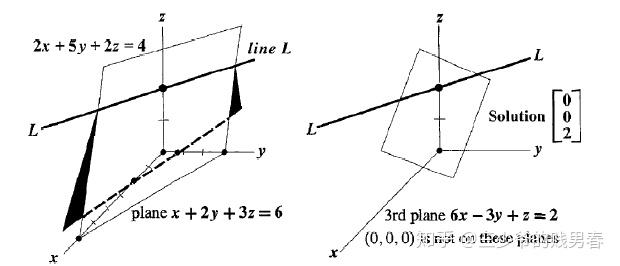
注:G. Strang 在授课中曾提及自身作图局限性,其教材中通过“两平面交线与第三平面相交”的分步图示展示解的存在性;而 D.C.Lay 的教材则通过单张图更简洁地呈现了三维平面的相交关系。
4.2 三元方程组的列图像
将系数矩阵按列分解,三元方程组的列图像形式为列向量的线性组合:
x⋅[126]+y⋅[25−3]+z⋅[321]=[642]x \cdot \begin{bmatrix} 1 \\ 2 \\ 6 \end{bmatrix} + y \cdot \begin{bmatrix} 2 \\ 5 \\ -3 \end{bmatrix} + z \cdot \begin{bmatrix} 3 \\ 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ 2 \end{bmatrix} x⋅126+y⋅25−3+z⋅321=642
其几何意义为:寻找标量 x,y,zx, y, zx,y,z,使得三个列向量分别数乘后相加得到 b\boldsymbol{b}b。下图为该线性组合的几何示意图:
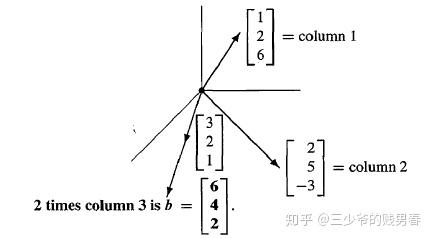
4.3 方程组解的存在性问题
对于三元方程组 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b,一个核心问题是:是否对所有的 b\boldsymbol{b}b,方程组均有解?
从列图像角度,该问题等价于:系数矩阵 A\boldsymbol{A}A 的列向量的线性组合是否能覆盖整个三维空间?
- 若三个列向量“线性无关”(即不存在一个列向量可由另外两个列向量线性表示),则其线性组合可覆盖整个三维空间,对任意 b\boldsymbol{b}b,方程组均有解;
- 若三个列向量“线性相关”(如列 3 = 列 1 + 列 2),则所有列向量共面,其线性组合仅能覆盖该平面。若 b\boldsymbol{b}b 不在此平面内,方程组无解。此时矩阵 A\boldsymbol{A}A 称为奇异矩阵(Singular Matrix) 或不可逆矩阵(Non-invertible Matrix)。
下图对比了 G. Strang 与 D.C.Lay 教材中对三元方程组行图像(平面相交关系)的作图差异:
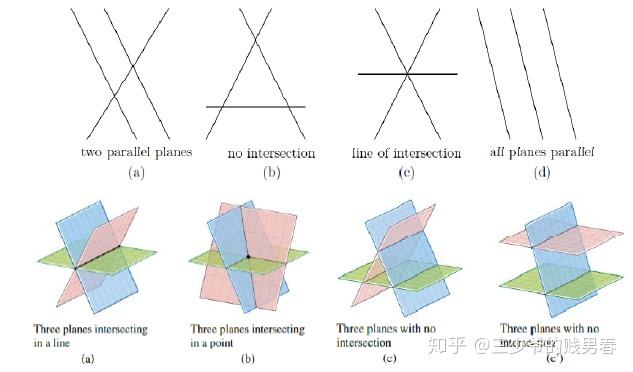
5 矩阵与向量的乘法规则
矩阵与向量的乘法 Ax\boldsymbol{A}\boldsymbol{x}Ax 有两种等价的计算方式,分别对应列图像与行图像的思想。
5.1 基于列向量线性组合的计算(列图像视角)
将矩阵 A\boldsymbol{A}A 按列分解为列向量,Ax\boldsymbol{A}\boldsymbol{x}Ax 即为列向量的线性组合。以矩阵 A=[2513]\boldsymbol{A} = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}A=[2153] 与向量 x=[12]\boldsymbol{x} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}x=[12] 为例:
Ax=[2513][12]=1⋅[21]+2⋅[53]=[2+101+6]=[127]\boldsymbol{A}\boldsymbol{x} = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = 1 \cdot \begin{bmatrix} 2 \\ 1 \end{bmatrix} + 2 \cdot \begin{bmatrix} 5 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 + 10 \\ 1 + 6 \end{bmatrix} = \begin{bmatrix} 12 \\ 7 \end{bmatrix} Ax=[2153][12]=1⋅[21]+2⋅[53]=[2+101+6]=[127]
5.2 基于行向量点积的计算(行图像视角)
将矩阵 A\boldsymbol{A}A 的每一行视为行向量,Ax\boldsymbol{A}\boldsymbol{x}Ax 的每个分量为对应行向量与 x\boldsymbol{x}x 的点积。仍以上述矩阵与向量为例:
Ax=[2513][12]=[(2⋅1+5⋅2)(1⋅1+3⋅2)]=[2+101+6]=[127]\boldsymbol{A}\boldsymbol{x} = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} (2 \cdot 1 + 5 \cdot 2) \\ (1 \cdot 1 + 3 \cdot 2) \end{bmatrix} = \begin{bmatrix} 2 + 10 \\ 1 + 6 \end{bmatrix} = \begin{bmatrix} 12 \\ 7 \end{bmatrix} Ax=[2153][12]=[(2⋅1+5⋅2)(1⋅1+3⋅2)]=[2+101+6]=[127]
两种计算方式的结果完全一致,分别从列图像(线性组合)与行图像(点积)的角度诠释了矩阵与向量乘法的本质。
矩阵的几何意义:行图像与列图像的系统解析
孙梓轩 编辑于 2025-08-08 10:10・美国
1. 行空间的几何意义与方程组解的关联
线性方程组的行图像,本质是将方程组中每个方程对应为其所在维度空间中的“解空间”,方程组的解即为所有解空间的交集。以下从二维情形出发,逐步剖析行图像的几何特征与方程组可解性的关系。
1.1 二元一次方程组的行图像示例(有解情形)
以二元一次方程组为例:
{x+2y=52x+3y=7\begin{cases} x + 2y = 5 \\ 2x + 3y = 7 \end{cases} {x+2y=52x+3y=7
该方程组中,每个方程对应 2 维空间(R2\mathbb{R}^2R2) 中的一条直线:
- 方程 x+2y=5x + 2y = 5x+2y=5 的解空间是一条斜率为 −12-\frac{1}{2}−21 的直线;
- 方程 2x+3y=72x + 3y = 72x+3y=7 的解空间是一条斜率为 −23-\frac{2}{3}−32 的直线。
两条直线的交点即为方程组的解(x=−1,y=3x = -1, y = 3x=−1,y=3)。从几何上看,只要不同方程对应的直线不平行,就存在唯一交点,方程组有唯一解。
需注意:直线在空间中沿其延伸方向无限延展,并非局限于有限坐标范围(如 x∈[−10,10],y∈[−10,10]x \in [-10,10], y\in [-10,10]x∈[−10,10],y∈[−10,10]),因此解的存在性仅由直线的相对位置决定,与坐标范围无关。
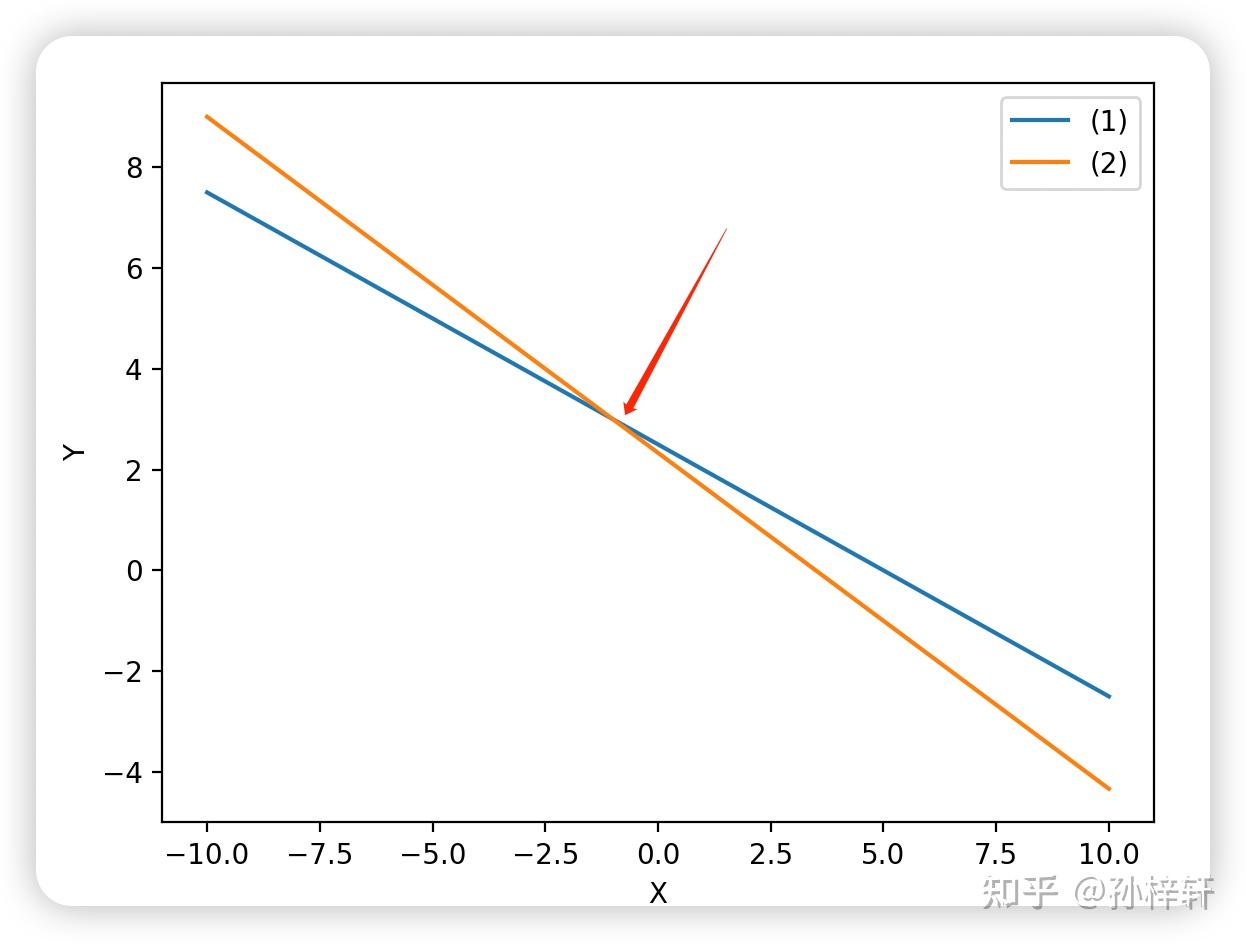
1.2 二元一次方程组的行图像示例(无解情形)
考虑无解的二元一次方程组:
{x+2y=52x+4y=7\begin{cases} x + 2y = 5 \\ 2x + 4y = 7 \end{cases} {x+2y=52x+4y=7
其对应的行图像为两条平行直线(斜率均为 −12-\frac{1}{2}−21),无任何交点,因此方程组无解。
从系数角度分析:两条直线平行的充要条件是“方程中未知数系数成比例,且常数项不成比例”。具体表现为系数矩阵的两行成比例——设系数矩阵 A=[a1b1a2b2]\boldsymbol{A} = \begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}A=[a1a2b1b2],则 a1a2=b1b2≠c1c2\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}a2a1=b2b1=c2c1($ c_1, c_2 $ 为常数项)。
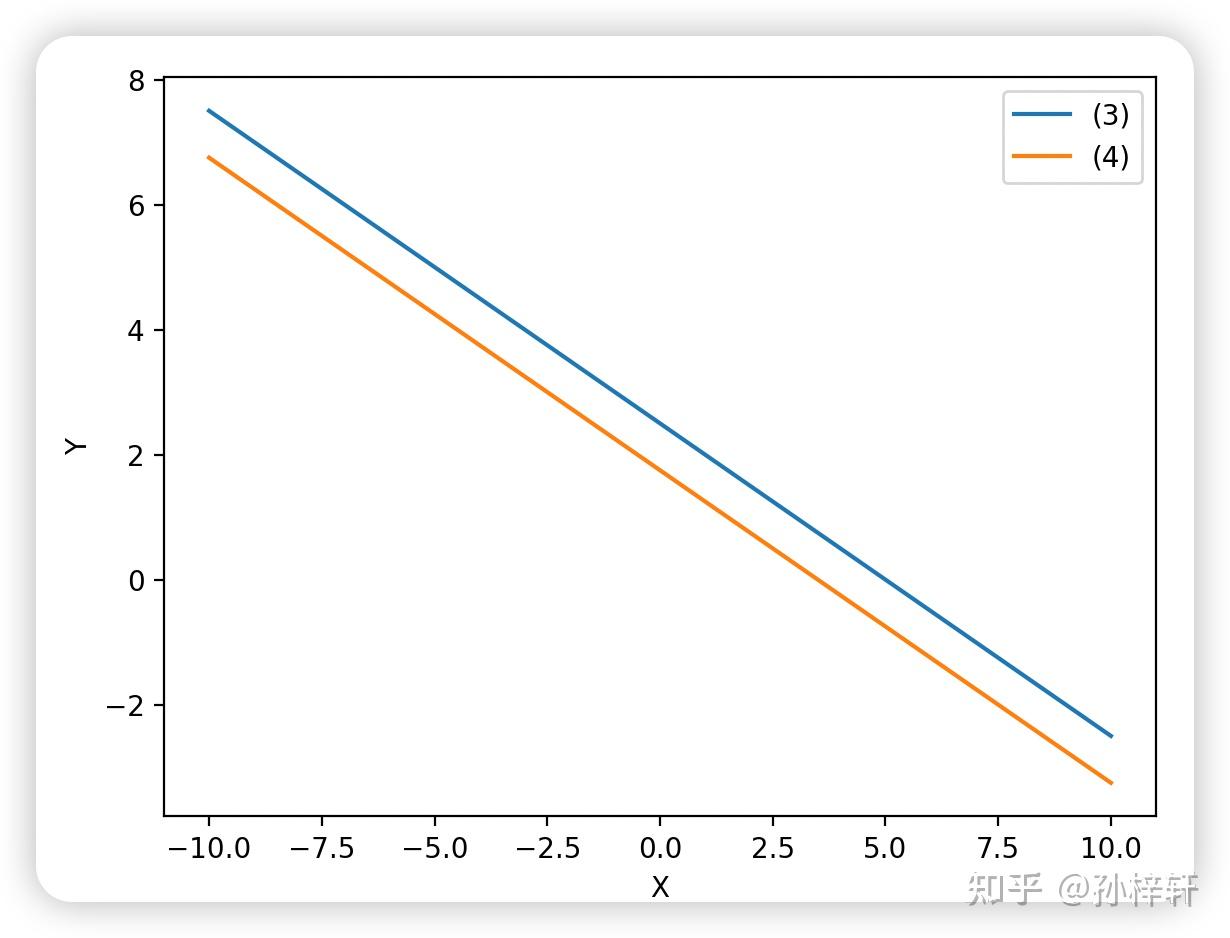
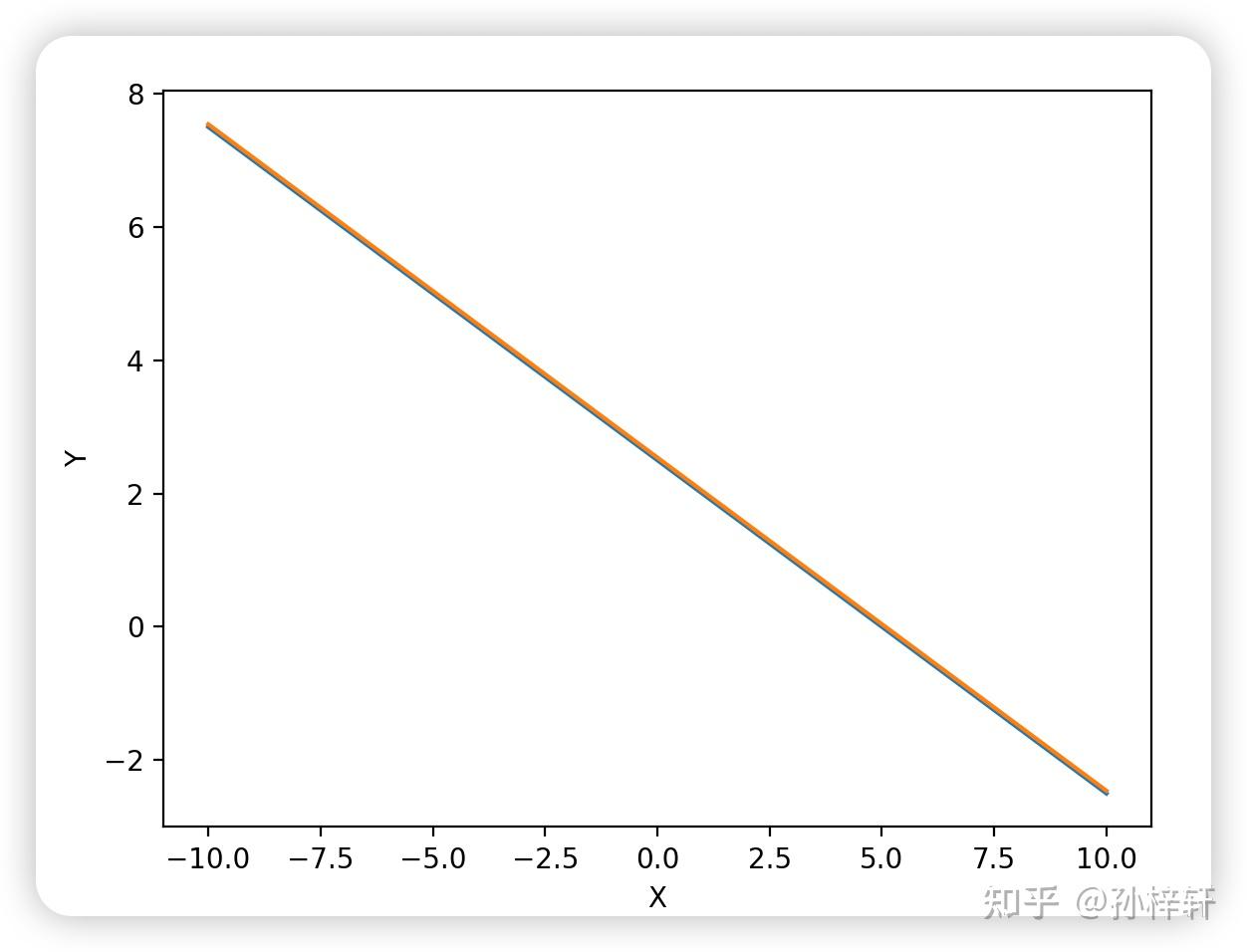
1.3 二元一次方程组的行图像示例(无穷多解情形)
若方程组满足“系数成比例且常数项成比例”,则对应的直线完全重合,解空间为整条直线,方程组有无穷多解。例如:
{x+2y=52x+4y=10\begin{cases} x + 2y = 5 \\ 2x + 4y = 10 \end{cases} {x+2y=52x+4y=10
系数矩阵 A=[1224]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}A=[1224] 的两行成比例(第二行是第一行的 2 倍),且常数项 555 与 101010 也成 2 倍比例,因此两条直线完全重合,所有满足 x+2y=5x + 2y = 5x+2y=5 的 (x,y)(x,y)(x,y) 均为解。
1.4 行向量的线性相关性与方程组可解性
将系数矩阵 A\boldsymbol{A}A 的每一行视为一个 行向量(如上述示例中,r1=[12],r2=[24]\boldsymbol{r}_1 = \begin{bmatrix} 1 & 2 \end{bmatrix}, \boldsymbol{r}_2 = \begin{bmatrix} 2 & 4 \end{bmatrix}r1=[12],r2=[24]),则:
- 若存在非零常数 kkk,使得 ri=k⋅rj\boldsymbol{r}_i = k \cdot \boldsymbol{r}_jri=k⋅rj(i≠ji \neq ji=j),则称这两个行向量 线性相关;
- 若不存在这样的 kkk,则称行向量 线性无关。
结合行图像的几何意义,可得出核心结论:
- 若系数矩阵 A\boldsymbol{A}A 的行向量 全部线性无关,则方程组 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 必有解(且解唯一,二维情形下直线不平行、不重合);
- 若存在线性相关的行向量,则方程组可能无解(系数成比例但常数项不成比例),也可能有无穷多解(系数与常数项均成比例)——线性相关是“方程组无解或无穷多解”的必要非充分条件。
1.5 高维情形的行图像推广
行图像的逻辑可自然推广至高维方程组:
- 三元一次方程(3 个未知数)对应的解空间是 3 维空间(R3\mathbb{R}^3R3) 中的一个平面;
- 四元一次方程对应的解空间是 4 维空间(R4\mathbb{R}^4R4) 中的一个“超平面”(无法直观作图,但可通过维度逻辑分析)。
高维方程组的解即为所有超平面(或平面)的交集:交集为一点则有唯一解,交集为一条直线/平面则有无穷多解,无交集则无解。
2. 列空间的几何意义与矩阵乘法的本质
列空间的核心是从“列向量线性组合”的视角理解矩阵乘法 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b,即将 Ax\boldsymbol{A}\boldsymbol{x}Ax 视为系数矩阵 A\boldsymbol{A}A 的列向量按 x\boldsymbol{x}x 的分量进行线性组合,最终得到 b\boldsymbol{b}b。
2.1 矩阵乘法的两种计算视角
对于矩阵乘法 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b(其中 A∈Rm×n,x∈Rn×1,b∈Rm×1\boldsymbol{A} \in \mathbb{R}^{m \times n}, \boldsymbol{x} \in \mathbb{R}^{n \times 1}, \boldsymbol{b} \in \mathbb{R}^{m \times 1}A∈Rm×n,x∈Rn×1,b∈Rm×1),存在两种等价的计算逻辑:
(1)行视角:行向量与列向量的点积
将 A\boldsymbol{A}A 的每一行视为行向量,与 x\boldsymbol{x}x(列向量)做点积,结果即为 b\boldsymbol{b}b 的对应分量。其通用公式为:
bi=∑k=1nAik⋅xk(i=1,2,…,m)b_i = \sum_{k=1}^n A_{ik} \cdot x_k \quad (i = 1,2,\dots,m) bi=k=1∑nAik⋅xk(i=1,2,…,m)
例如,对于 A=[1223],x=[xy]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}, \boldsymbol{x} = \begin{bmatrix} x \\ y \end{bmatrix}A=[1223],x=[xy],则:
b1=[12]⋅[xy]=x+2y,b2=[23]⋅[xy]=2x+3yb_1 = \begin{bmatrix} 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = x + 2y, \quad b_2 = \begin{bmatrix} 2 & 3 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = 2x + 3y b1=[12]⋅[xy]=x+2y,b2=[23]⋅[xy]=2x+3y
(2)列视角:列向量的线性组合
将 A\boldsymbol{A}A 的每一列视为列向量,以 x\boldsymbol{x}x 的分量为系数,对列向量进行线性组合,结果即为 b\boldsymbol{b}b。形式化表示为:
Ax=x1⋅a1+x2⋅a2+⋯+xn⋅an=b\boldsymbol{A}\boldsymbol{x} = x_1 \cdot \boldsymbol{a}_1 + x_2 \cdot \boldsymbol{a}_2 + \dots + x_n \cdot \boldsymbol{a}_n = \boldsymbol{b} Ax=x1⋅a1+x2⋅a2+⋯+xn⋅an=b
其中 ak=[A1kA2k⋮Amk]\boldsymbol{a}_k = \begin{bmatrix} A_{1k} \\ A_{2k} \\ \vdots \\ A_{mk} \end{bmatrix}ak=A1kA2k⋮Amk(A\boldsymbol{A}A 的第 kkk 列列向量),xkx_kxk 为 x\boldsymbol{x}x 的第 kkk 个分量。
以 A=[1223],x=[−13]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}, \boldsymbol{x} = \begin{bmatrix} -1 \\ 3 \end{bmatrix}A=[1223],x=[−13] 为例:
Ax=(−1)⋅[12]+3⋅[23]=[−1+6−2+9]=[57]=b\boldsymbol{A}\boldsymbol{x} = (-1) \cdot \begin{bmatrix} 1 \\ 2 \end{bmatrix} + 3 \cdot \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 + 6 \\ -2 + 9 \end{bmatrix} = \begin{bmatrix} 5 \\ 7 \end{bmatrix} = \boldsymbol{b} Ax=(−1)⋅[12]+3⋅[23]=[−1+6−2+9]=[57]=b
2.2 列图像的几何直观:线性组合的可视化
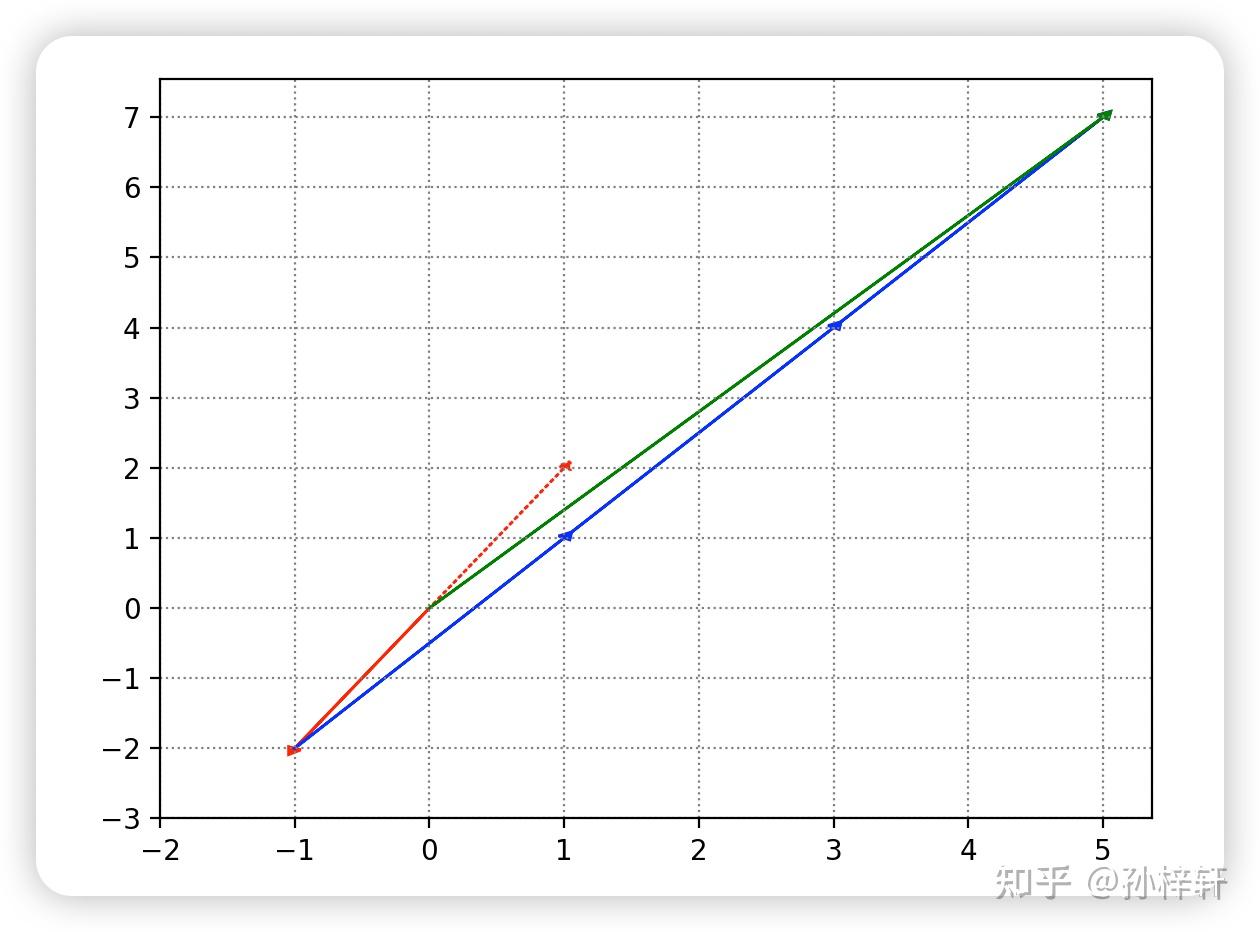
列图像的本质是将“列向量线性组合得到 b\boldsymbol{b}b”的过程可视化。以上述示例为例,其几何意义如下:
- 列向量 a1=[12]\boldsymbol{a}_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix}a1=[12](红色虚线向量)经数乘 −1-1−1 后,方向反向,得到 −1⋅a1=[−1−2]-1 \cdot \boldsymbol{a}_1 = \begin{bmatrix} -1 \\ -2 \end{bmatrix}−1⋅a1=[−1−2](红色实线向量);
- 列向量 a2=[23]\boldsymbol{a}_2 = \begin{bmatrix} 2 \\ 3 \end{bmatrix}a2=[23](蓝色向量)经数乘 333 后,长度伸展为原来的 3 倍,得到 3⋅a2=[69]3 \cdot \boldsymbol{a}_2 = \begin{bmatrix} 6 \\ 9 \end{bmatrix}3⋅a2=[69];
- 将两个数乘后的向量相加(遵循向量加法的“三角形法则”),最终得到 b=[57]\boldsymbol{b} = \begin{bmatrix} 5 \\ 7 \end{bmatrix}b=[57](绿色向量)。
2.3 列向量的线性相关性与方程组可解性
列向量的线性相关性决定了“列向量线性组合能否覆盖整个目标空间”,进而决定方程组 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 是否有解。
(1)线性相关与线性无关的定义
对于 Rm\mathbb{R}^mRm 中的 nnn 个列向量 a1,a2,…,an\boldsymbol{a}_1, \boldsymbol{a}_2, \dots, \boldsymbol{a}_na1,a2,…,an:
- 若存在不全为零的常数 k1,k2,…,knk_1, k_2, \dots, k_nk1,k2,…,kn,使得 k1a1+k2a2+⋯+knan=0k_1\boldsymbol{a}_1 + k_2\boldsymbol{a}_2 + \dots + k_n\boldsymbol{a}_n = \boldsymbol{0}k1a1+k2a2+⋯+knan=0,则称这 nnn 个列向量 线性相关;
- 若仅当 k1=k2=⋯=kn=0k_1 = k_2 = \dots = k_n = 0k1=k2=⋯=kn=0 时上式成立,则称列向量 线性无关。
几何上,二维空间中两个列向量线性相关等价于“两向量共线”(方向相同或相反);三维空间中三个列向量线性相关等价于“三向量共面”。
(2)列向量线性无关的充要条件与方程组可解性
核心结论:若系数矩阵 A\boldsymbol{A}A 的列向量 全部线性无关,则对任意 b∈Rm\boldsymbol{b} \in \mathbb{R}^mb∈Rm,方程组 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 必有解。
原因如下:线性无关的列向量其线性组合可“充满”整个目标空间(如二维空间中,不共线的两个向量可组合出平面内所有向量;三维空间中,不共面的三个向量可组合出空间内所有向量)。因此,任意 b\boldsymbol{b}b 均可由这些列向量的线性组合表示,即存在对应的 x\boldsymbol{x}x 满足 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b。
若列向量线性相关(如二维空间中两向量共线),则其线性组合仅能覆盖一条直线(无法充满整个平面):
- 若 b\boldsymbol{b}b 在这条直线上,则方程组有解(无穷多解);
- 若 b\boldsymbol{b}b 不在这条直线上,则方程组无解。
2.4 行向量与列向量线性相关性的一致性
对于任意矩阵 A\boldsymbol{A}A,其行向量的线性相关性与列向量的线性相关性具有 一致性:
- 若 A\boldsymbol{A}A 的行向量全部线性无关,则其列向量也全部线性无关;
- 若 A\boldsymbol{A}A 存在线性相关的行向量,则其列向量也存在线性相关。
例如:
- 矩阵 A=[1224]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}A=[1224] 的行向量线性相关(第二行是第一行的 2 倍),列向量也线性相关(第二列是第一列的 2 倍);
- 矩阵 A=[1223]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}A=[1223] 的行向量线性无关,列向量也线性无关。
这一一致性是后续“矩阵秩”概念的核心基础(矩阵的行秩等于列秩)。
3. 解空间的维度与自由度
方程组解空间的维度(如直线、平面)本质是“自由度”的体现——自由度即“确定解所需独立变量的个数”,解空间的维度等于自由度。
3.1 自由度与解空间维度的关系
以方程对应的解空间为例:
- 二元一次方程 y=ax+by = ax + by=ax+b(或 ax+by+c=0ax + by + c = 0ax+by+c=0):确定解 (x,y)(x,y)(x,y) 时,只需任意指定 xxx 的值,即可唯一确定 yyy 的值,因此 自由度为 1,解空间为 1 维(直线);
- 三元一次方程 z=ax+by+cz = ax + by + cz=ax+by+c(或 ax+by+cz+d=0ax + by + cz + d = 0ax+by+cz+d=0):确定解 (x,y,z)(x,y,z)(x,y,z) 时,需任意指定 xxx 和 yyy 的值,即可唯一确定 zzz 的值,因此 自由度为 2,解空间为 2 维(平面);
- nnn 元一次方程:自由度为 n−1n-1n−1,解空间为 n−1n-1n−1 维(超平面)。
本质上,方程的作用是“约束一个维度”,使原 nnn 维空间的解空间降维为 n−1n-1n−1 维。
由上述方程可知,其中一个维度的取值(一个未知变量对应一个维度,如前文的 yyy 和 zzz 可由其余两个维度的取值(对应未知变量)唯一确定。当其余两个维度对应的未知变量取值确定时,该维度的取值也随之确定,即此维度不具备自由度。
具体而言,前文两个方程中:
- 二元一次方程的自由度为 1;
- 三元一次方程的自由度为 2。
从空间维度与自由度的对应关系来看:
- 二维空间的自由度为 2;
- 三维空间的自由度为 3。
而上述方程对应的自由度(1 和 2)均低于其所在空间的自由度,因此方程的解空间发生维度退化(简称“降维”):
- 二元一次方程的解空间退化为自由度为 1 的空间,几何形态表现为一条直线;
- 三元一次方程的解空间退化为自由度为 2 的空间,几何形态表现为一个平面。
3.2 自由度与方程组解的个数
方程组解的个数由“所有方程约束后的总自由度”决定:
- 若总自由度为 0(如两个不平行的二元一次方程,约束两个维度),则解空间为 0 维(一个点),方程组有唯一解;
- 若总自由度为 k>0k > 0k>0(如两个重合的二元一次方程,仅约束一个维度),则解空间为 kkk 维(一条直线或平面),方程组有无穷多解;
- 若方程之间存在矛盾(如两个平行的二元一次方程),则无满足所有约束的解,方程组无解。
4. 最后
本文通过行图像与列图像的双视角,揭示了矩阵的几何意义与方程组可解性的核心逻辑,关键结论可概括为:
- 行图像:方程组的解是各方程对应解空间(直线、平面或超平面)的交集,解的存在性由行向量的线性相关性决定;
- 列图像:矩阵乘法 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 是列向量的线性组合,解的存在性由列向量的线性相关性决定;
- 一致性:矩阵的行向量与列向量线性相关性一致,这是“矩阵秩”的核心属性。
上述提到的方程组是否一定有解、维度、矩阵的秩(rank,反映线性无关向量的最大个数)以及矩阵是否可逆(方程组有唯一解的特殊情形),都是有相关性的。
via:
-
MIT线性代数笔记一 行图像和列图像_为什么行图和列图维度不一样-CSDN博客
https://blog.csdn.net/herosunly/article/details/88698381- ref
- Gilbert Strang. Introduction to Linear Algebra (5th Edition). Wellesley-Cambridge Press.
- David C. Lay. Linear Algebra and Its Applications (5th Edition). Pearson.
- deep learning - Hung-yi Lee
https://speech.ee.ntu.edu.tw/~tlkagk/courses_ML19.html - 麻省理工 线性代数 (MIT 18.06, Linear Algebra, Gilbert Strang)【中英】_bilibili
https://www.bilibili.com/video/av34573725/ - 哈尔滨工业大学 矩阵分析 全72讲 主讲-严质彬 视频教程_bilibili
https://www.bilibili.com/video/av11355346/
- ref
-
MIT—线性代数笔记01 行图像和列图像 - 知乎
https://zhuanlan.zhihu.com/p/45708880 -
矩阵的几何意义(行图像和列图像) - 知乎
https://zhuanlan.zhihu.com/p/618370114













 在Window 系统的默认安装配置)


,js(基本类型、运算符典例))
)

)