Scikit-learn Python机器学习 - 分类算法

锋哥原创的Scikit-learn Python机器学习视频教程：

https://www.bilibili.com/video/BV11reUzEEPH

课程介绍

本课程主要讲解基于Scikit-learn的Python机器学习知识，包括机器学习概述，特征工程(数据集，特征抽取，特征预处理，特征降维等)，分类算法(K-临近算法，朴素贝叶斯算法，决策树等)，回归与聚类算法(线性回归，欠拟合，逻辑回归与二分类，K-means算法)等。

Scikit-learn Python机器学习 - 分类算法 - 朴素贝叶斯

什么是贝叶斯公式？

在学习朴素贝叶斯之前，我们必须先掌握贝叶斯公式

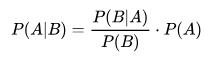
这个公式乍一看，你肯定很懵逼，不过不用怕，我们来解释和分解下，你就懂了。

这些符号是什么意思？

P(A|B)：在 B 已经发生的情况下，A 发生的概率。这是我们想求的，叫做后验概率（更新后的信念）。
P(B|A)：在 A 已经发生的情况下，B 发生的概率。这个通常我们从数据中能得到，叫做似然概率。
P(A)：在不知道任何证据（B）的情况下，A 发生的概率。这是我们最初的看法，叫做先验概率。
P(B)：B 发生的总概率，叫做证据或标准化常量。

我们来推导一下贝叶斯公式

P(AB)=P(A)*P(B|A) A和B同时发生的概率等于P(A)乘以P(B|A)，这个大家应该能理解。

同理 P(AB)=P(B)*P(A|B) A和B同时发生的概率也等于P(B)乘以P(A|B)，相信这个大家也应该能理解。

所以我们能推导出 P(A) * P(B|A) = P(B) * P(A|B) 把右边的P(B)放到左边去就推导出了贝叶斯公式。相当大家彻底理解了贝叶斯公式。

贝叶斯公式经典实例-疾病的检测

这是一个非常著名且反直觉的例子，能完美展示贝叶斯思想的威力。

场景： 假设某种疾病在人群中的发病率是 1%（先验知识）。现在有一种检测方法：

如果你确实有病，检测结果呈阳性（True Positive）的概率是 99%（非常准）。
如果你没有病，检测结果呈阳性（False Positive）的概率是 5%（有5%的误诊率）。

问题： 如果一个人去做了检测，结果是阳性，那么他真正患病的概率到底是多少？

很多人会直觉地认为是99%或者95%，但贝叶斯定理会给我们一个出乎意料的答案。

首先，定义事件：

A：真正患病
B：检测结果为阳性

我们要求的是：在检测结果为阳性的情况下，真正患病的概率，即 P(患病 | 阳性)，也就是 P(A|B)。

根据公式，我们需要知道：

P(A) - 先验概率：在不知道检测结果时，一个人患病的概率 = 发病率 = 1% = 0.01
P(B|A) - 似然概率：如果一个人真有病，检测为阳性的概率 = 99% = 0.99
P(B) - 证据：检测结果为阳性的总概率。这个需要计算一下。

计算 P(B)： 一个人检测为阳性有两种可能：

他真有病，并且检测对了：(0.01 * 0.99)
他其实没病，但被误诊了：((1 - 0.01) * 0.05)

所以，P(B) = (真有病且测出阳性) + (真没病但误诊为阳性) P(B) = (0.01 * 0.99) + (0.99 * 0.05) P(B) = 0.0099 + 0.0495 P(B) = 0.0594

现在，将所有值代入贝叶斯公式：

P(A|B) =0.99/0.0594*0.01=0.1667

结论： 即使检测结果是阳性，你真正患病的概率也只有大约 16.67%！

什么是朴素贝叶斯算法？

朴素贝叶斯（Naive Bayes）算法 是一种基于贝叶斯定理的分类方法，广泛应用于文本分类（如垃圾邮件识别、情感分析等）和其他机器学习领域。它的核心假设是 特征与特征之间条件相互独立，即在给定类别的条件下，特征之间没有任何关系或依赖。

朴素贝叶斯公式

在给定数据集的条件下，朴素贝叶斯定理的公式可以用贝叶斯公式推导出来。假设我们有一个样本

，这些是特征（例如文本中的单词频率、图像的像素等）。目标是通过这些特征来预测一个类别 C 。

朴素贝叶斯的优缺点

优点：

简洁高效：朴素贝叶斯方法实现简单，训练和预测速度都非常快。
适合高维数据：对于特征维度很高的数据（如文本分类），朴素贝叶斯特别适用，因为它能有效处理大量的特征。
良好的性能：在许多实际问题中，朴素贝叶斯能够取得不错的分类效果，特别是在数据特征间独立性假设基本成立的情况下。

缺点：

条件独立假设过于简单：实际数据中，特征之间往往存在依赖关系，而朴素贝叶斯假设特征之间完全独立，这可能会影响其性能。
对稀疏数据敏感：如果某个类别中某个特征从未出现过，朴素贝叶斯会计算出零概率，导致预测失败。为了解决这个问题，通常采用平滑技术（如拉普拉斯平滑）来避免零概率的问题。

朴素贝叶斯算法 在实际应用中有着广泛的使用，尤其适用于文本分类、垃圾邮件检测、情感分析、推荐系统等任务。由于其计算简单、高效并且能够处理大规模数据，朴素贝叶斯常常成为一些领域中首选的算法之一。

朴素贝叶斯算法具体Scikit-learn实例-新闻文本分类预测

MultinomialNB 是 Scikit-learn 中用于多项式分布数据的朴素贝叶斯分类器，特别适合文本分类等离散特征计数的场景。下面我将详细解释其构造方法、参数、属性和方法。

构造方法：

MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)

参数详解：

alpha : float, 默认=1.0

含义：平滑参数（拉普拉斯平滑/Lidstone平滑）
作用：防止概率计算中出现零值的问题
详细解释：
- 当某个特征在某个类别中从未出现时，概率会变为0，导致整个后验概率为0
- alpha=1 是拉普拉斯平滑（加1平滑）
- 0 < alpha < 1 是Lidstone平滑
- alpha=0 表示不使用平滑（可能导致过拟合和零概率问题）
数学公式：
- 平滑后的条件概率：P(x_i|y) = (N_{yi} + α) / (N_y + α × n)
- 其中 N_{yi} 是特征 i 在类别 y 中的出现次数，N_y 是类别 y 中所有特征的出现次数，n 是特征数量
建议值：通常使用1.0，可以通过交叉验证调整

fit_prior : bool, 默认=True

含义：是否学习类别先验概率
作用：控制是否使用训练数据中的类别分布
详细解释：
- fit_prior=True：使用训练数据中的类别频率作为先验概率
- fit_prior=False：使用均匀先验概率（所有类别概率相等）
数学公式：
- 当 fit_prior=True：P(y) = N_y / N
- 当 fit_prior=False：P(y) = 1 / k (k为类别数)
适用场景：
- 当训练集类别分布能代表真实分布时，使用True
- 当训练集类别不平衡或不能代表真实分布时，可考虑使用False

class_prior : array-like of shape (n_classes,), 默认=None

含义：类别的先验概率
作用：手动指定各类别的先验概率
详细解释：
- 如果指定了此参数，fit_prior参数将被忽略
- 数组长度必须等于类别数量
- 概率值应该总和为1（但算法会自动归一化）
示例：对于二分类问题，可以设置class_prior=[0.7, 0.3]

我们来看下具体示例：

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics import accuracy_score, classification_report
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB# 1,加载数据
news = fetch_20newsgroups(subset='all')# 2,数据预处理
X_train, X_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.2)  # 划分训练集和测试集tfidfVectorizer = TfidfVectorizer()  # 特征抽取 TF-IDF
X_train_scaled = tfidfVectorizer.fit_transform(X_train)  # fit计算生成模型
X_test_scaled = tfidfVectorizer.transform(X_test)  # # 使用训练集的参数转换测试集# 3,创建和训练LogisticRegression模型
model = MultinomialNB()
model.fit(X_train_scaled, y_train)  # 使用训练数据拟合（训练）模型# 4,进行预测并评估模型
y_pred = model.predict(X_test_scaled)  # 在测试集上进行预测
print('模型预测值：', y_pred)
print('正确值   ：', y_test)accuracy = accuracy_score(y_test, y_pred)  # 计算准确率
print(f'测试集准确率：{accuracy:.2f}')
print('分类报告：\n', classification_report(y_test, y_pred, target_names=news.target_names))

运行结果：

模型预测值： [ 0 18 11 ...  5 15 10]
正确值   ： [ 0 18 11 ...  5  2  9]
测试集准确率：0.85
分类报告：precision    recall  f1-score   supportalt.atheism       0.91      0.73      0.81       170comp.graphics       0.87      0.77      0.81       193comp.os.ms-windows.misc       0.87      0.80      0.83       192
comp.sys.ibm.pc.hardware       0.68      0.88      0.77       181comp.sys.mac.hardware       0.97      0.86      0.91       205comp.windows.x       0.95      0.86      0.90       205misc.forsale       0.90      0.70      0.79       185rec.autos       0.93      0.89      0.91       205rec.motorcycles       0.95      0.96      0.95       206rec.sport.baseball       0.95      0.94      0.94       194rec.sport.hockey       0.91      0.98      0.94       200sci.crypt       0.78      0.97      0.86       200sci.electronics       0.92      0.86      0.89       188sci.med       0.97      0.86      0.92       200sci.space       0.89      0.97      0.93       199soc.religion.christian       0.56      0.99      0.72       203talk.politics.guns       0.69      0.97      0.81       163talk.politics.mideast       0.95      0.97      0.96       205talk.politics.misc       1.00      0.53      0.69       158talk.religion.misc       1.00      0.21      0.35       118accuracy                           0.85      3770macro avg       0.88      0.84      0.84      3770weighted avg       0.88      0.85      0.85      3770Process finished with exit code 0