引言
上节我们学习完二叉树后[数据结构——lesson9.二叉树],这节我们将学习数据结构——堆
学习目标
1.堆的概念及结构
堆是一种特殊的完全二叉树结构,在计算机科学和数据结构中广泛应用,特别是在堆排序算法和优先队列的实现中,堆可以通过数组来表示,这种表示方式利用了完全二叉树的性质,即除了最后一层外,每一层都被完全填满,并且所有节点都尽可能地向左对齐。
1.1堆的概念
堆通常是一个可以被看作一棵完全二叉树的数组对象,若满足:
(1)任意节点的值>=其子节点的值。则称为大根堆。
(2)任意节点的值<=其子节点的值。则称为小根堆。
1.2堆的结构
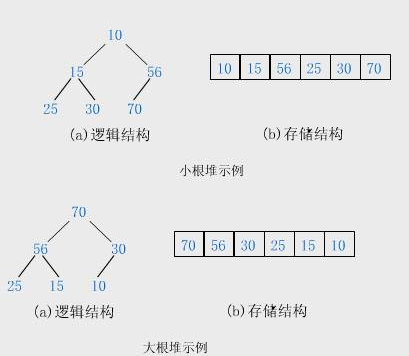
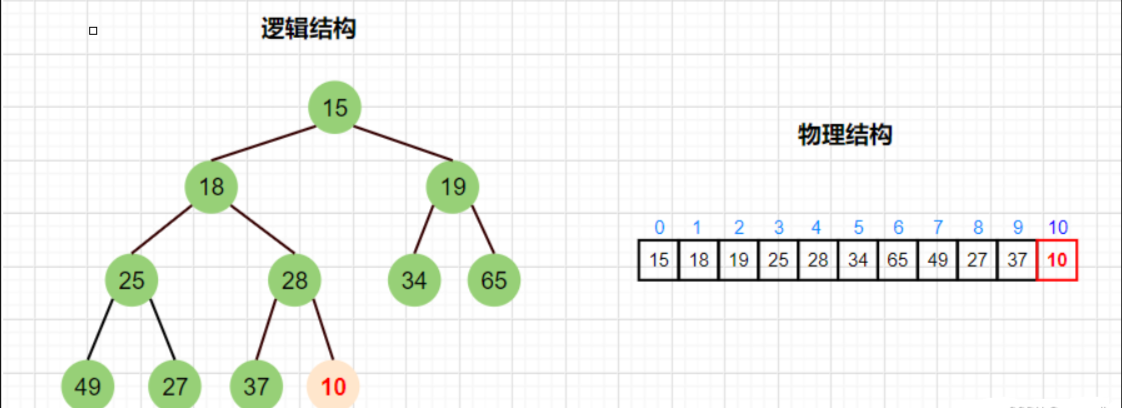
- 逻辑结构:堆是一棵完全二叉树,除了最后一层外,每一层都被完全填满,并且所有节点都尽可能地向左对齐。
- 物理结构:堆在物理上通常采用顺序存储,即使用数组来表示。根节点位于数组的第一个位置(下标通常为 0 或 1)。对于下标从 1 开始的数组,任意节点 i 的左子节点为 2i,右子节点为 2i+1;对于下标从 0 开始的数组,左子节点为 2i+1,右子节点为 2i+2。通过这种方式,可以利用数组的随机访问特性高效地模拟树的结构。
如图所示:
操作系统和数据结构这两门学科中都有栈和堆的概念,如何区分 ❓
数据结构角度
- 栈:是一种运算受限的线性表2。只允许在表的一端进行插入和删除操作,遵循后进先出(LIFO)原则。主要操作有入栈(Push)和出栈(Pop)。可使用数组或链表作为底层数据结构,分别称为顺序栈和链式栈。
- 堆:是一种特殊的树形数据结构。通常可分为最大堆和最小堆,最大堆中父节点的值大于等于子节点的值,最小堆中父节点的值小于等于子节点的值。主要操作包括插入元素和删除堆顶元素等,并需重新调整堆的结构。常用于实现优先队列、堆排序等。
操作系统角度
- 栈:是进程地址空间中的一块区域,用于存储函数调用时的局部变量、函数参数和返回地址等信息。其内存由操作系统自动分配和释放,函数调用时压栈,函数返回时弹栈。栈的大小有限,一般每个进程的栈大小相对较小,如 64 位 Linux 系统默认栈大小通常为 10MB。内存地址生长方向是从高地址向低地址增长。
- 堆:也是进程地址空间中的一部分,用于动态内存分配。程序运行时通过 malloc 或 new 等函数分配内存,大小可变。内存由程序员手动管理,需调用相应函数释放内存,否则易引发内存泄漏。堆的内存地址通常从低地址向高地址增长,由于是通过分散的内存块管理,其内存空间在物理上不连续,频繁操作可能产生内存碎片。
二者联系

1.3堆的调整算法
在实现堆的结构之前我们先要了解一下堆的调整算法
1.堆的数值交换
思路:堆的交换还是比较简单的,跟之前写的没什么区别,记得传地址。
void swap(HPDatatype* x, HPDatatype* y) {int temp = 0;temp = *x;*x = *y;*y = temp; }2.堆的向上调整算法 (应用于堆的数据插入)
此算法是为了确保插入数据后的堆依然是符合堆的性质而单独封装出来的函数,就好比如我们后续要插入的数字10(小堆)
- 基本思路:将新增元素插入到堆数组的末尾,然后将该元素与其父结点进行比较。若该元素的值小于父结点的值(小根堆)或大于父结点的值(大根堆),则交换两者的位置,之后将原父结点当作新的目标结点,继续向上进行比较和交换操作,直到该元素的值不小于父结点的值(小根堆)或不大于父结点的值(大根堆),或者到达根节点为止。
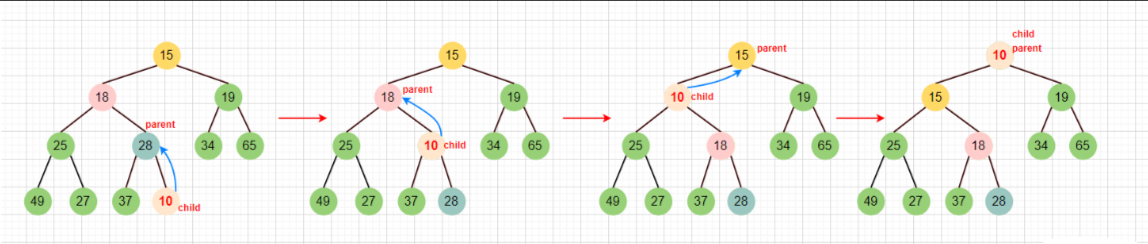
为了确保在插入数字10后依然是个小根堆,所以要将10和28交换,依次比较父结点parent和子结点child的大小,当父小于子结点的时候,就返回,反之就一直交换,直到根部while(child>0)截止。
:由前文的得知的规律,parent = (child - 1) / 2,我们操控的是数组,但要把它想象成二叉树。画图演示调整过程:
代码实现:
// 向上调整函数(没有改变动态数组的首地址,不需要用指针传输) // 时间复杂度O(logN) // 传入了 动态数组 和 最后一个位置的下标(也就是孩子的下标) // 向上调整的条件;上面的数据是堆 void AdjustUp(HPDatatype* a, int child) {// 计算父亲的小标int parent = (child - 1) / 2;// 当 child 的小标大于 0 就继续 (也就小于是根节点位置)while (child > 0){// 小堆 <// 大堆 >if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}} }核心逻辑:
- 计算父节点下标:parent = (child - 1) / 2
- 循环比较子节点与父节点的值
- 如果子节点值小于父节点值(符合小堆特性),则交换两者位置
- 更新子节点和父节点下标,继续向上比较
- 当子节点成为根节点(child > 0不成立)或满足堆特性时,循环结束
3.堆的向下调整算法(应用于堆的数据删除)
此算法是为了确保删除数据后的堆依然是符合堆的性质而单独封装出来的函数,就好比如我们后续要删除数字10(小堆)
- 基本思路:首先将堆顶元素与堆中最后一个元素进行交换,然后删除最后一个元素(此时堆顶元素为原来的堆尾元素)。接着从堆顶开始,将堆顶元素与它的子节点进行比较,如果子节点中有比它更小(小根堆)或更大(大根堆)的元素,则将堆顶元素与该子节点交换位置,之后继续以交换后的位置为新的 “堆顶”,重复上述比较和交换操作,直到满足堆的性质为止。
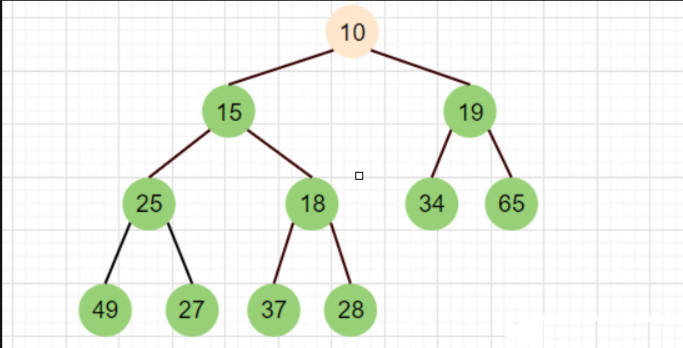
如下图:
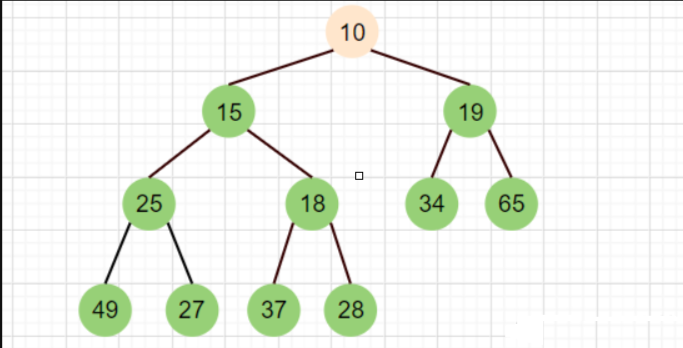
(我们这里首先将堆顶元素(10)与堆中最后一个元素进行交换(28),然后删除最后一个元素(10))
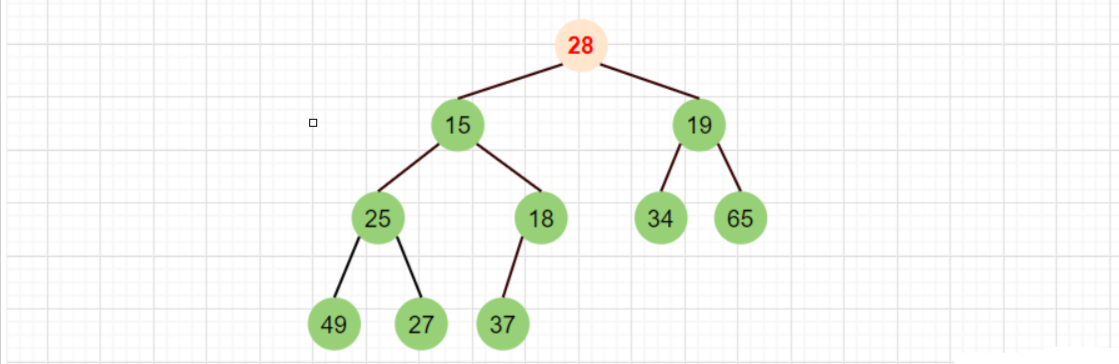
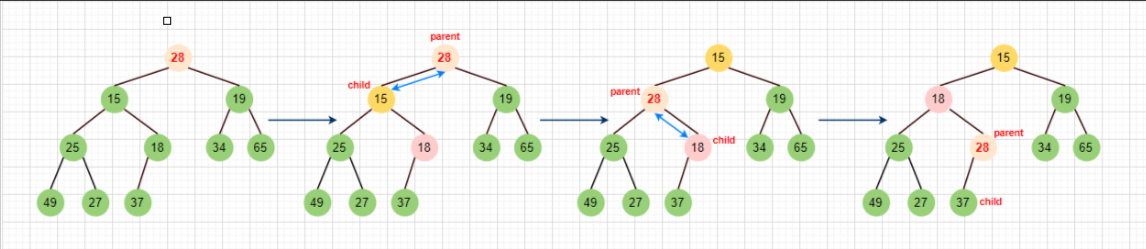
此时我们看到,这个二叉树整体上不符合堆的性质,但是其根部的左子树和右子树均满足堆的性质。 接下来,就要进行向下调整,确保其最终是个堆。只需三部曲。
▶:找出左右孩子中最小的那个
▶:跟父亲比较,如果比父亲小,就交换
▶:再从交换的孩子位置继续往下调整
代码实现:
// 向下调整 // 向下调整的前提:后面的数据是堆 void AdjustDown(HPDatatype* a, int n, int parent) {// 左孩子int child = parent * 2 + 1;// 孩子可能会超出数组范围while (child < n){// 如果右孩子小于左孩子// 找出小的那个孩子// 保证右孩子存在且不越界// 大堆 >// 小堆 <if (child + 1 < n && a[child+1] < a[child]){//跳转到有孩子那里child++;}// 开始向下调整// 大堆 >// 小堆 <if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}} }核心逻辑:
- 先计算左孩子下标:child = parent * 2 + 1
- 循环条件:孩子下标小于总元素个数(未超出边界)
- 首先判断是否存在右孩子,并且比较左右孩子大小,选择较小的那个孩子(小堆特性)
- 比较父节点与选中的孩子节点值,如果孩子值更小,则交换两者位置
- 更新父节点和孩子节点下标,继续向下比较
- 当父节点满足堆特性或没有孩子节点时,循环结束
2.堆的实现方式
虽然堆是一种特殊的二叉树,它既可以用数组存储也可以用链式存储。但是考虑到其完全二叉树的特性,我们在这里采用数组存储的方式,因为这样既方便访问,也并不会浪费格外的空间。
数组与堆的映射关系(这里实现根的下标为0):
1.若某节点在数组中的下标为i(i从0开始),则其左子节点(若存在)的下标为2i+1,右子节点(若存在)的下标为2i+2,其父节点(若存在)的下标为(i-1)/2。
2.堆的根节点在数组的下标为0。
2.1堆的声明
由于我们使用数组来实现堆,因此堆的声明与顺序表类似。

2.2堆的功能实现
注意:我们这里实现的是小根堆(大根堆实现原理一样)
我们要实现的堆的基本功能:
1.堆的初始化
2.堆的插入
3.堆的删除
4.获取堆顶的元素
5.堆的元素个数
6.堆的判空
7.销毁堆

2.2.1堆的初始化
(1)代码实现
// 堆的初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}🧐🧐🧐堆的核心功能
2.2.2堆的插入
(1)代码实现
思路:堆的插入不像先前顺序表一般,可以头插,任意位置插入等等,因为是堆,要符合大根堆或小根堆的性质,不能改变堆原本的结构,所以尾插才是最适合的,并且尾插后还要检查是否符合堆的性质。
- 尾插的原因:堆一般使用数组存储,完全二叉树的结点从上到下、从左到右依次连续,用数组存储不会浪费空间。在数组尾部插入数据的时间复杂度是 O (1),效率较高。若采用头插或其他任意位置插入,会破坏堆的完全二叉树结构,导致难以高效地维护堆的性质,所以尾插是最适合堆的插入方式。
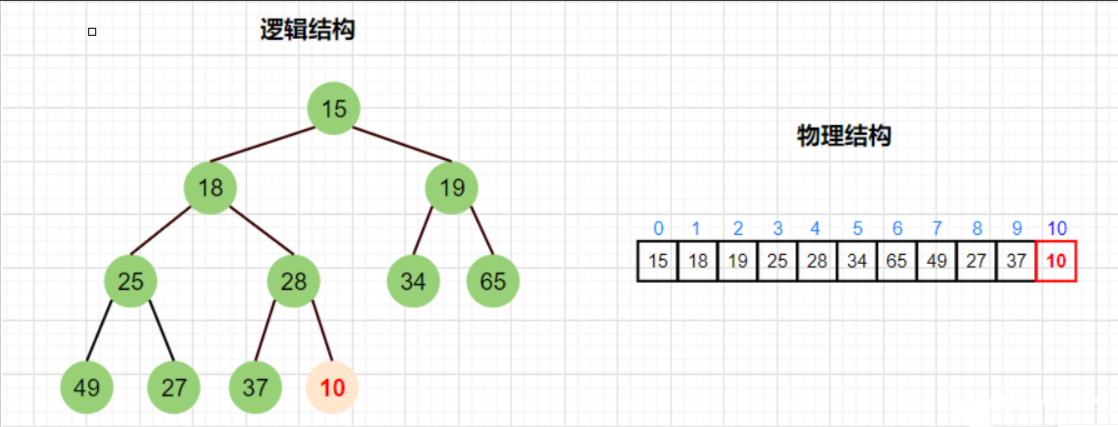
比如我们有一串数组,该数组是按照小根堆的性质存储的。现在想在数组尾部插入一个数字10,如图:
这颗树在没插入数字10之前是个小堆,在插入后就不是了,改变了小根堆的性质了。因为子结点10小于其父结点28。
首先最基本的,在插入之前就要先判断该堆的容量是否还够插入数据,先检查要不要扩容,扩容完毕后。我们可以发现,插入的10只会影响到从自己本身开始到根,也就是祖先,只要这条路上符合堆的性质,插入即成功。
核心思想:向上调整算法。当我们看到插入的10比父亲28小时,此时交换数字,但是此时10又要比18小,再次交换,最终发现10比15还小,再次交换,此时结束,到根部了。当然这是最坏的情况,如果在中间换的过程中满足了堆的性质,那么就不需要再换了,直接返回即可。这就叫向上调整算法,直接套用上面的函数即可。
代码如下:
// 交换 void Swap(HPDataType* p1, HPDataType* p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp; }// 堆向上调整 void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}} } // 堆插入数据 void HPPush(HP* php, HPDataType x) {assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1); }2.2.3堆的删除
思路:在上文堆的插入中,我们明确插完依旧是堆,而这里堆的删除同样也要确保删除后依旧是堆,注意:这里堆的删除是删除堆顶的数据。以小根堆为例,删除堆顶的数据,也就是把最小的数据删掉,那么还要保证依旧是堆
如果我们直接删除堆顶元素并往前覆盖就可能打乱原有的亲缘关系。所以我们可以先将堆顶的元素与末尾元素交换,然后再进行向下调整·。
- 首先,把第一个数据和最后一个数据进行交换
- 交换后,此时的堆就不符合其性质了,因为原先最后一个数据肯定是比第一个数据大的,现在最后一个数据到了堆顶,就不是堆了,但是根结点的左子树和右子树不受影响,单独看它们依旧是堆
- 接着,--size,确保删除堆顶数据
- 因为此时堆顶的数据已经到了堆尾,只需要像顺序表那样--size,确保有效数据减1也就是确保了堆顶的删除
- 最后,运用向下调整算法,确保其是堆结构
(1)代码实现
// 堆向下调整 void AdjustDown(HPDataType* a, int n, int parent) {// 假设左孩子比右孩子小int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}} }// 删除堆顶数据 void HPPop(HP* php) {assert(php);assert(php->size > 0);// 将堆顶元素(即php->a[0])与堆的最后一个元素交换Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0); }
5.4.获取堆顶的元素
思路:直接返回堆顶即可。前提是得断言size>0
(1)代码实现
// 读取堆顶数据
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}5.6.堆的判空
思路:堆的判空很简单,跟之前栈顺序表一样,若size为0,直接返回即可。
(1)代码实现
// 判断堆是否为空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}5.7.销毁堆
(1)代码实现
// 堆的销毁
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}5.8堆的构建
对于堆的创建这一块,有两种方法,一种是直接利用我们上面所写的【Init】和【Push】联合向上调整建堆;另一种则是利用数据拷贝进行向下调整建堆
方法1
- 首先我们来看第一种。很简单,就是利用【Init】和【Push】联合向上调整进行建堆
/*建堆*/
void HeapCreate1(Hp* hp, HpDataType* a, int n)
{assert(hp);HeapInit(hp);for (int i = 0; i < n; ++i){HeapPush(hp, a[i]);}
}
方法2✅
- 接着是第二种,比较复杂一些,不会像【向上调整算法】一样插入一个调整一个,而是为这个堆的存放数据的地方单独开辟出一块空间,然后将数组中的内容拷贝过来,这里使用到了memcpy,不懂的小伙伴可以先去了解一下它的用法
当把这些数据都拿过来之后,我们去整体性地做一个调整,那就不可以做向上调整了,需要去进行一个【向下调整】,我们通过图解来看看
HeapInit(hp);
HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * n); //首先申请n个空间用来存放原来的堆
if (tmp == NULL)
{perror("fail malloc");exit(-1);
}
hp->a = tmp;//void * memcpy ( void * destination, const void * source, size_t num );
memcpy(hp->a, a, sizeof(HpDataType) * n); //将数组a中n个数据拷贝到堆中的数组
hp->size = n;
hp->capacity = n;
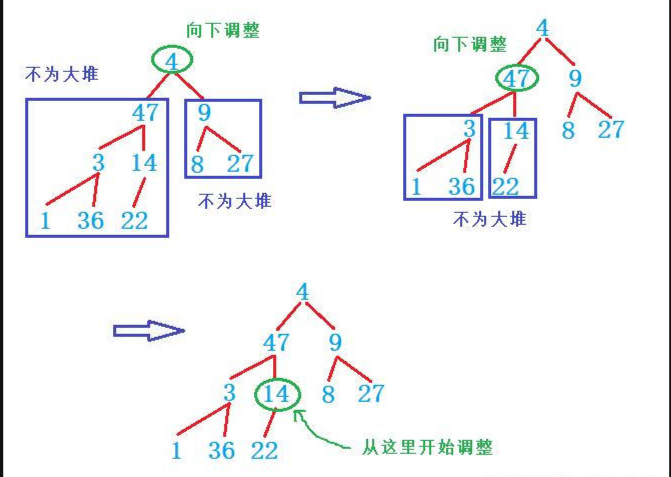
- 可以看到,对于即将要调整的根结点,首先我们要回忆一下向下调整算法的先决条件,就是当要调整的结点的左右子树均为大堆或者小堆,只有待调整的结点不满足时,才可以使用这个算法,但是可以看到,【4】下面的两个子树均不是大堆(我这里默认建大堆),那有同学说这该怎么办呢?此时我们应该先去调整其左右子树,使他们先符合条件才行
- 然后可以看到左子树这一边,当【47】作为要调整的结点时,它的左右子树依旧不是一个大堆,此时我们需要做的就是再去调整其左右子树,直到其符合条件为止,那此时我们应该去调整【3】【14】,那还需要再去调整其左右子树吗?可以看到【1】和【36】确实也是不符合,但是呢对于叶子结点来说是没有孩子的,所以调不调整都一个样,因此我们只需要从倒数第二层开始调整就行,也就是最后一个非叶子结点,即【14】
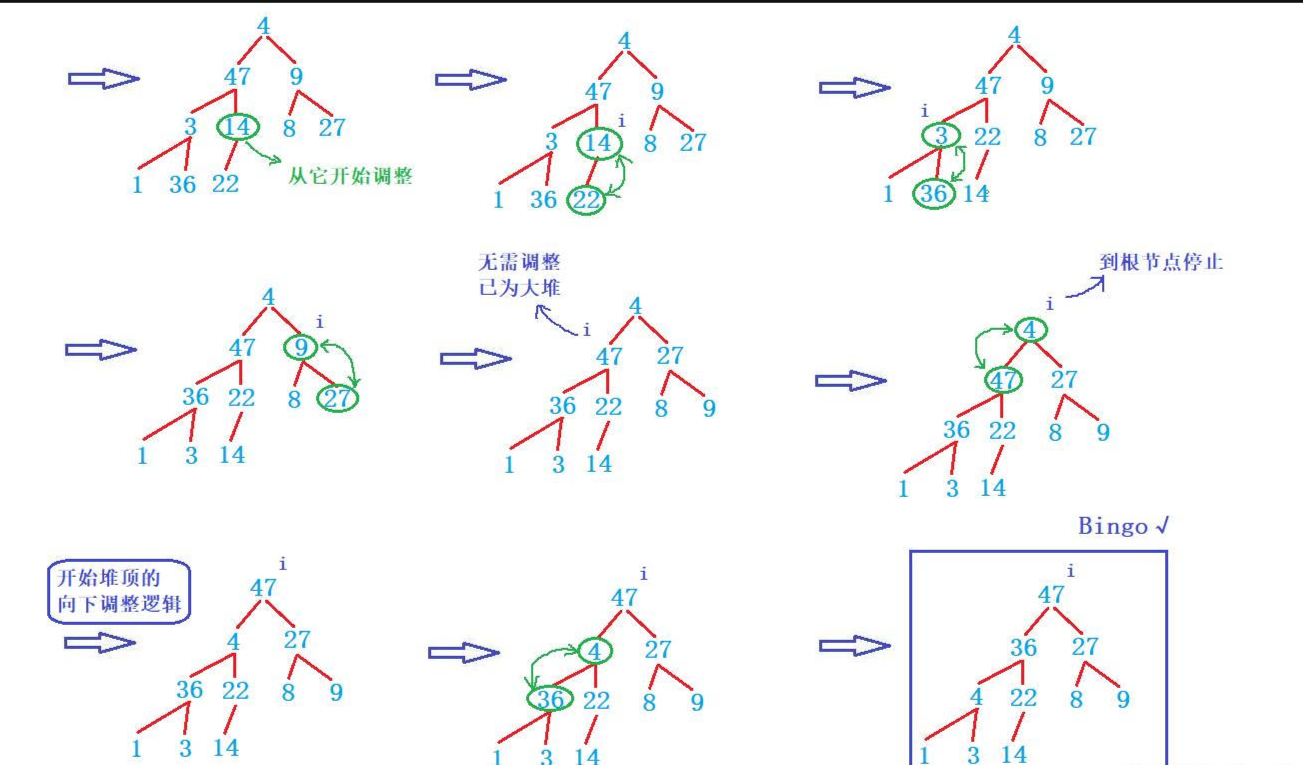
- 那要如何去找到和这个【14】呢,这个好办,我们可以知道它的孩子,就是堆底的末梢元素,那对于数组来说最后一个数据的下标为【n - 1】,在上面有说到过已知孩子结点去求结点其父亲结点【(child - 1)/2】,那这里的【child】我们使用【n - 1】带入即可,然后通过循环来一直进行调整,但是在调整完【14】这棵子树后要怎么越位到【3】这棵子树呢,上面说到了,堆存放在一个数组中,因此我们直接将这个【parent - 1】就可以继续往前调整了。最后直到根节点为止就是我们上面讲解【向下调整算法】时的样子
//向下调整 /* * (n - 1)代表取到数组最后一个数据,不可以访问n * (x - 1)/2 代表通过孩子找父亲 */ for (int i = ((n - 1) - 1) / 2; i >= 0; --i) {Adjust_Down(hp->a, n, i); } - 下面是【向下调整算法建堆】执行的全过程
完整代码
// 堆结构体定义(底层是动态数组)
typedef int HpDataType;
typedef struct Heap {HpDataType* a; // 存储堆元素的数组int size; // 当前堆中元素个数int capacity; // 堆的最大容量
} Hp;// Way2:基于数组拷贝+向下调整的建堆函数
void HeapCreate2(Hp* hp, HpDataType* a, int n) {assert(hp); // 断言堆指针非空,避免非法访问HeapInit(hp); // 先初始化堆(将a置NULL,size和capacity置0)// 步骤1:为堆数组开辟内存(大小为n个HpDataType)HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * n);if (tmp == NULL) { // 检查内存开辟是否成功perror("fail malloc"); // 打印错误信息exit(-1); // 终止程序(内存开辟失败无法继续)}hp->a = tmp; // 将开辟的内存地址赋值给堆的数组指针// 步骤2:拷贝原数组a的n个元素到堆数组hp->a中memcpy(hp->a, a, sizeof(HpDataType) * n); // 说明:memcpy(dest, src, num),num=元素大小*个数,确保拷贝所有元素// 步骤3:更新堆的size和capacity(此时堆已有n个元素,容量为n)hp->size = n;hp->capacity = n;// 步骤4:从最后一个非叶子节点开始,逐个向下调整// 计算最后一个非叶子节点的下标:(n-2)/2for (int i = ((n - 1) - 1) / 2; i >= 0; --i) {Adjust_Down(hp->a, hp->size, i); // 对每个节点i执行向下调整}
}// 向下调整算法(核心依赖,建大堆为例)
void Adjust_Down(int* a, int n, int parent) {int child = parent * 2 + 1; // 先假设左孩子是较大的子节点while (child < n) { // 循环条件:孩子节点存在(未越界)// 1. 找到左右孩子中较大的那个(需先判断右孩子是否存在)if (child + 1 < n && a[child + 1] > a[child]) {++child; // 右孩子存在且更大,切换到右孩子}// 2. 比较父节点与较大孩子:若父节点小,则交换并继续向下调整if (a[child] > a[parent]) {swap(&a[child], &a[parent]); // 交换父子节点(swap是自定义交换函数)parent = child; // 父节点下移到交换后的孩子位置child = parent * 2 + 1; // 重新计算新的左孩子位置} else {break; // 父节点 >= 孩子,当前子树已符合堆性质,退出循环}}
}Way2 的关键优势:效率远高于 Way1
Way2 的核心优势体现在时间复杂度上:
| 建堆方式 | 时间复杂度 | 核心原因 |
| Way1(向上调整) | O(NlogN) | 每个元素插入时需向上调整,平均调整次数为树的高度(logN),N 个元素总复杂度为 N*logN |
| Way2(向下调整) | O(N) | 从最后一个非叶子节点开始调整,底层节点(数量多)调整次数少(1 次),顶层节点(数量少)调整次数多(logN 次),通过错位相减计算总次数约为 N |
完整代码
Heap.h
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void Swap(HPDataType* p1, HPDataType* p2);
void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);void HPInit(HP* php);
void HPDestroy(HP* php);
void HPPush(HP* php, HPDataType x);
void HPPop(HP* php);
HPDataType HPTop(HP* php);
bool HPEmpty(HP* php);
int HeapSize(HP* php);Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"// 交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 堆向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//堆向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{//先假设左孩子比右孩子小int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//堆的初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//堆的销毁
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}// 删除堆顶数据
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}//读取堆顶数据
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//判断堆是否为空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}// 获取堆的个数
int HeapSize(HP* php)
{assert(php);return php->size;
}测试用例:
void TestHeap()
{HP hp;HPInit(&hp);if (HPEmpty(&hp)){printf("堆空\n");}else{printf("堆非空\n");}int a[] = { 4,2,8,1,5,6,9,7,3,2,23,55,232,66,222,33,7,1,66,3333,999 };for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&hp, a[i]);}if (HPEmpty(&hp)){printf("堆空\n");}else{printf("堆非空\n");}printf("堆的数据个数:%d\n", HeapSize(&hp));while (!HPEmpty(&hp)){printf("%d ", HPTop(&hp));HPPop(&hp);}printf("\n");printf("堆的数据个数:%d\n", HeapSize(&hp));HPDestroy(&hp);
}输出结果:

结束语:
本节我们学习了新的二叉树——堆,接下来还会继续更新对数据结构-------堆的应用(排序,TopK问题)
感谢您的三连支持!!!




算法在民航LPV-200进近中的具体实现流程)







 进程基础)






)
(网络层、网段划分))
和animation(动画)——CSS)