前言

在学习动态规划时切忌望文生义，因为其名字与其思想关系不大，你可以自己想一个记住其思想的名字，例如：递推公式法，状态转移方程法等等。与其说动态规划是一个算法，还不如说是解决问题的方法论，动态规划的一般形式就是求最优值，比如最长公共子序列，最大子段和，最优二叉搜索树等等。

贪心算法：在前面我们提到过的Prim算法和Kruskal算法就借用到了贪心算法的思想，例如我们的Prim算法，每次我们都选择选中的顶点中的边的最小值，但是有一定的条件：选择出来的边不能闭环，像这种前一步的贪心和后一步的贪心没有直接关系就比较简单一点，例如一个序列中找最大值，最小值。

分治算法：大问题拆分成小问题，小问题之间相对独立，每个小问题解决方案是一样的

动态规划：大问题拆分成小问题，小问题之间互相依赖重复，每个小问题解决方案是一样的。

1.基本思想

动态规划算法与分治法类似，其基本思想就是将待求解问题分解成若干子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

与分治法不同的是，适合动态规划法求解的问题，经分解得到的子问题往往不是相互独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，以至于最后解决原问题需要耗费指数时间。然而，不同子问题的数目常常只有多项式量级。

在用分治法求解时，有些子问题被重复结算了很多次。如果我们能够保存已经解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，从而得到多项式时间复杂度的算法。为了达到此目的，可以用一个表来记录所有已解决的子问题的答案，不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划的基本思想。

基本要点：将待求解问题分解成若干子问题，先求解子问题，然后从这些子问题的解得到原问题的解；经分解得到的子问题往往不是相互独立的；保存已经解决的子问题的答案，避免重复计算。

例如下图我们想要f(N)的数据，假设需要知道f(x)和f(y)，f(x)需要从f(x1)得知，f(y)需要从f(x2)得知，而f(x2)和f(x1)有关，那我们就可以采用动态规划的思想，把f(x1)计算出的结果保存下来，这样计算f(x2)的时候就可以少计算一次f(x1)。

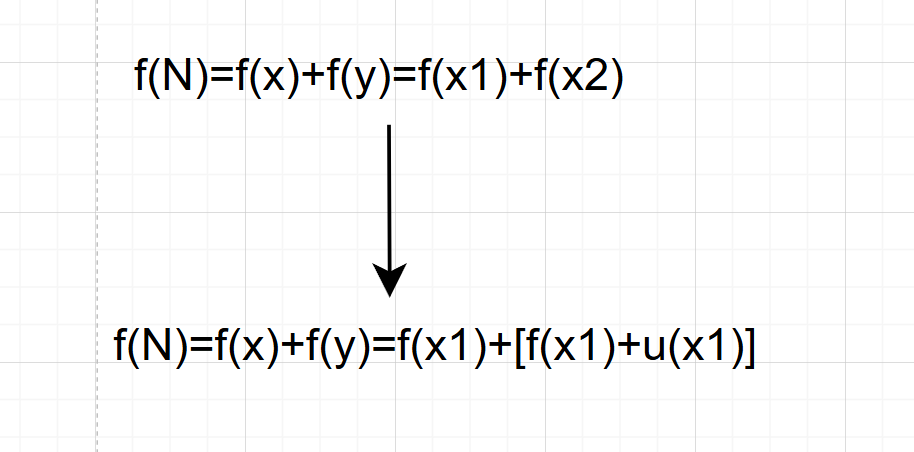
2.重叠子问题

在用递归算法自顶向下解决一个问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。动态规划正是利用了这种子问题的重叠性质，对每个子问题只解一次，而后将其解保存到一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。

动态规划经分解得到的子问题往往不是相互独立的 。如果经分解得到的子问题的解之间相互独立，比如二分查找（Binary Search）经分解得到的子问题之间相互独立，不存在重叠子问题，所以不适合用动态规划，更适合分治算法。

接下来来看一个非常经典的重叠子问题：斐波那契数列。

3.斐波那契数列

我们可以理解斐波那契数列为:f(n)=f(n-1)+f(n-2)（递推公式）。一个数字等于前面两个数字的和，这就是一个大问题拆分成几个小问题，我们需要把它拆分成递归搜索树。

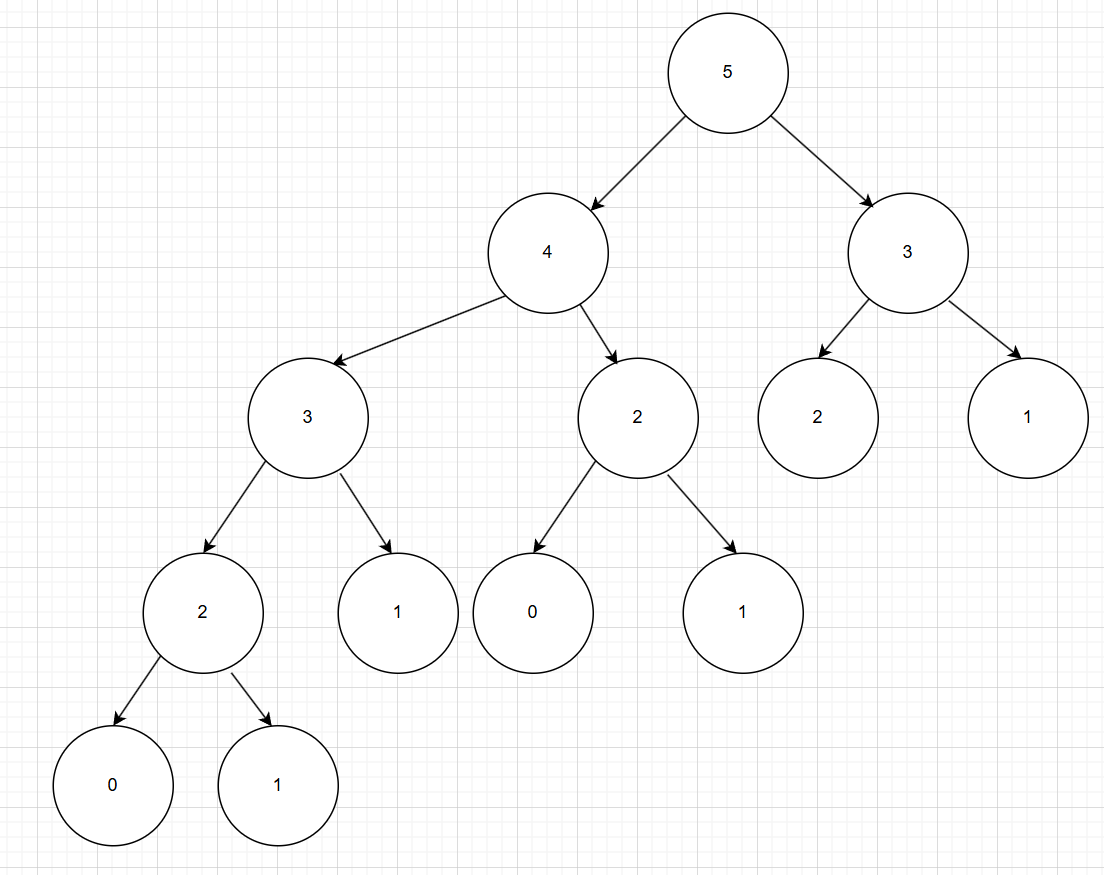
如图，如果我们想知道斐波那契数列中的第5个数字，我们需要知道第3个和第4个数字，一次向下类推可以得到一颗二叉树，明显到当我们拆分到2的时候，我们向下再拆一次就变成了需要知道0和1的问题，此时无法再向下拆分，我们就认为，0和1是初始状态（你也可以认为是1和2），当我们计算从下往上运算的时候，如果我们不保存已经计算得到的结果的话，我们会大量重复的计算，例如：先看5的左子树我们通过计算0，1计算2，再通过2，1计算3，此时3的右边2我们还需要重复计算，因为我们没有保存第一次计算得到的2的数值，同理当我们计算到4的时候，我们还需要计算得到5的右子树的3，因为我们没有保存第一次计算3时得到的数值，接下来看一看如果我们不保存值的话的时间长短。

这就是一个很简单的递归代码，我就不过多叙述

#include <stdio.h>
#include <time.h>
#include <stdlib.h>unsigned int fib01(unsigned int n) {if (n == 0) {return 0;}if (n == 1) {return 1;}return fib01(n - 1) + fib01(n - 2);
}// 1 1 2 3 5
void test01() {clock_t start = clock();unsigned int x = fib01(40);clock_t end = clock();printf("cost time: %f s。fib01 = %u\n", (double)(end - start) / CLOCKS_PER_SEC, x);
}int main() {test01();return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\06_DP\fib.exe
cost time: 0.504000 s。fib01 = 102334155进程已结束，退出代码为 0

现在将数字改为46

#include <stdio.h>
#include <time.h>
#include <stdlib.h>unsigned int fib01(unsigned int n) {if (n == 0) {return 0;}if (n == 1) {return 1;}return fib01(n - 1) + fib01(n - 2);
}// 1 1 2 3 5
void test01() {clock_t start = clock();unsigned int x = fib01(46);clock_t end = clock();printf("cost time: %f s。fib01 = %u\n", (double)(end - start) / CLOCKS_PER_SEC, x);
}int main() {test01();return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\06_DP\fib.exe
cost time: 8.964000 s。fib01 = 1836311903进程已结束，退出代码为 0

可以看到仅仅只是增加了6个数字，时间一下子增加了8秒之多，这是因为，我们每增加一个，都会多重复计算两层的数字，时间复杂度近似于n²。

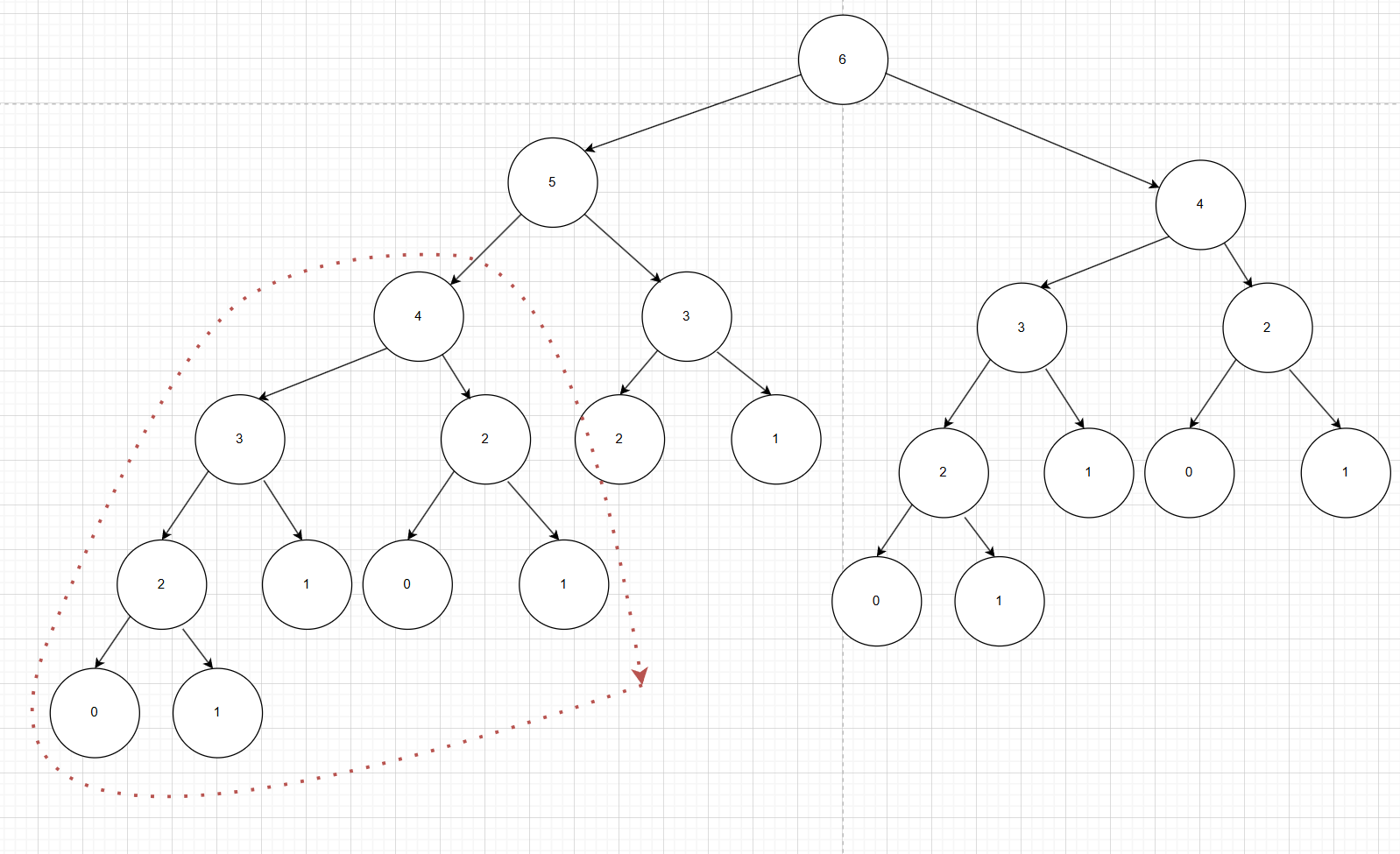
我们有两种方法解决这种问题，第一种是备忘录（记忆化搜索表），第二种是DP table，第一种方法是把大问题拆分成小问题，自顶向下解决问题，而第二种方法是拿到一个大问题，先想有哪些小问题需要我们解决，是自底向上解决问题。两种方法的时间复杂度都差不多，但第一种思路显然更符合人类的思考方式，所以如果是竞赛的同学多考虑第一种方法。

4.备忘录（记忆化搜索表）

备忘录方法为每一个子问题建立一个记录项，初始时，该记录项存入一个特殊的值，表示该子问题尚未被解决（比如斐波那契数的备忘录版本中将其设置为-1）。

在求解过程中，对每个待求解的子问题，首先查看其相应的记录项。若记录项中存储的是初始化时存入的特殊值，则表示该子问题是第一次遇到，此时计算出该子问题的解，并保存在相应的记录项中，以备以后查看。若记录项中存储的已不是初始化时存入的特殊值，则表示该子问题已被计算过，其相应的记录项存储的是该子问题的答 案。此时，只要从记录项中取出该子问题的答案即可，而不必重新计算。

4.1备忘录（记忆化搜索表）代码实现

#include <stdio.h>
#include <time.h>
#include <stdlib.h>// mem1[i] 记忆了第i个斐波那契数列的值
static unsigned int *mem1;
unsigned int fib02(unsigned int n) {if (n == 0) {return 0;}if (n == 1) {return 1;}if (mem1[n] == -1) {mem1[n] = fib02(n - 1) + fib02(n - 2);}return mem1[n];
}void test02() {int n = 46;mem1 = malloc(sizeof(unsigned int) * (n + 1));// 初始化这个表里，存储一个以后算法中永远不会出现的状态for (int i = 0; i <= n; ++i) {mem1[i] = -1;		}clock_t start = clock();unsigned int x = fib02(n);clock_t end = clock();printf("cost time: %f s。fib02 = %u\n", (double)(end - start) / CLOCKS_PER_SEC, x);free(mem1);
}

结果：

D:\work\DataStruct\cmake-build-debug\06_DP\fib.exe
cost time: 0.000000 s。fib02 = 1836311903进程已结束，退出代码为 0

可以看到，用的时间极短，我们存储了已经计过的值后，当遇到相同的值时我们直接返回就行不再需要重复计算，这大大减少了递归搜索树的节点，所以时间效率很高。

5.DP table

DP table就是动态规划算法自底向上建立的一个表格，用于保存每一个子问题的解，并返回表中的最后一个解。比如斐波那契数，我们先计算 fib(0)，然后 fib(1)，然后 fib(2)，然后 fib(3)，以此类推，直至计算出fib(n)。

比如我们计算 fib(5)，先由 fib(0) + fib(1) 得到 fib(2)，再由 fib(1) + fib(2) 得到 fib(3)，再由 fib(2) + fib(3) 得到 fib(4)，最后由 fib(3) + fib(4) 得到 fib(5)。

也就是说，我们只需要存储子问题的解，而不需要重复计算子问题的解。

5.1DP table代码实现

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
unsigned int fib03(unsigned int n) {unsigned int *mem = malloc(sizeof(unsigned int) * (n + 1));//递推mem[0] = 0;mem[1] = 1;for (int i = 2; i <= n; ++i) {mem[i] = mem[i - 1] + mem[i - 2];}unsigned int result = mem[n];free(mem);return result;
}void test03() {int n = 146;clock_t start = clock();unsigned int x = fib03(n);clock_t end = clock();printf("cost time: %f s。fib03 = %u\n", (double)(end - start) / CLOCKS_PER_SEC, x);
}int main() {test03();return 0;
}

D:\work\DataStruct\cmake-build-debug\06_DP\fib.exe
cost time: 0.000000 s。fib03 = 2620762145进程已结束，退出代码为 0

可以看到即使数字变成了146，我们的时间效率还是很高，因为我们已经保存了很多节点的数字。

6.练习

问题描述：给定三个数{1，3，5}，请问使用这三个数，有多少种方式可以构造出一个给定的数n（假设这里n等于6）（允许重复和不同顺序）

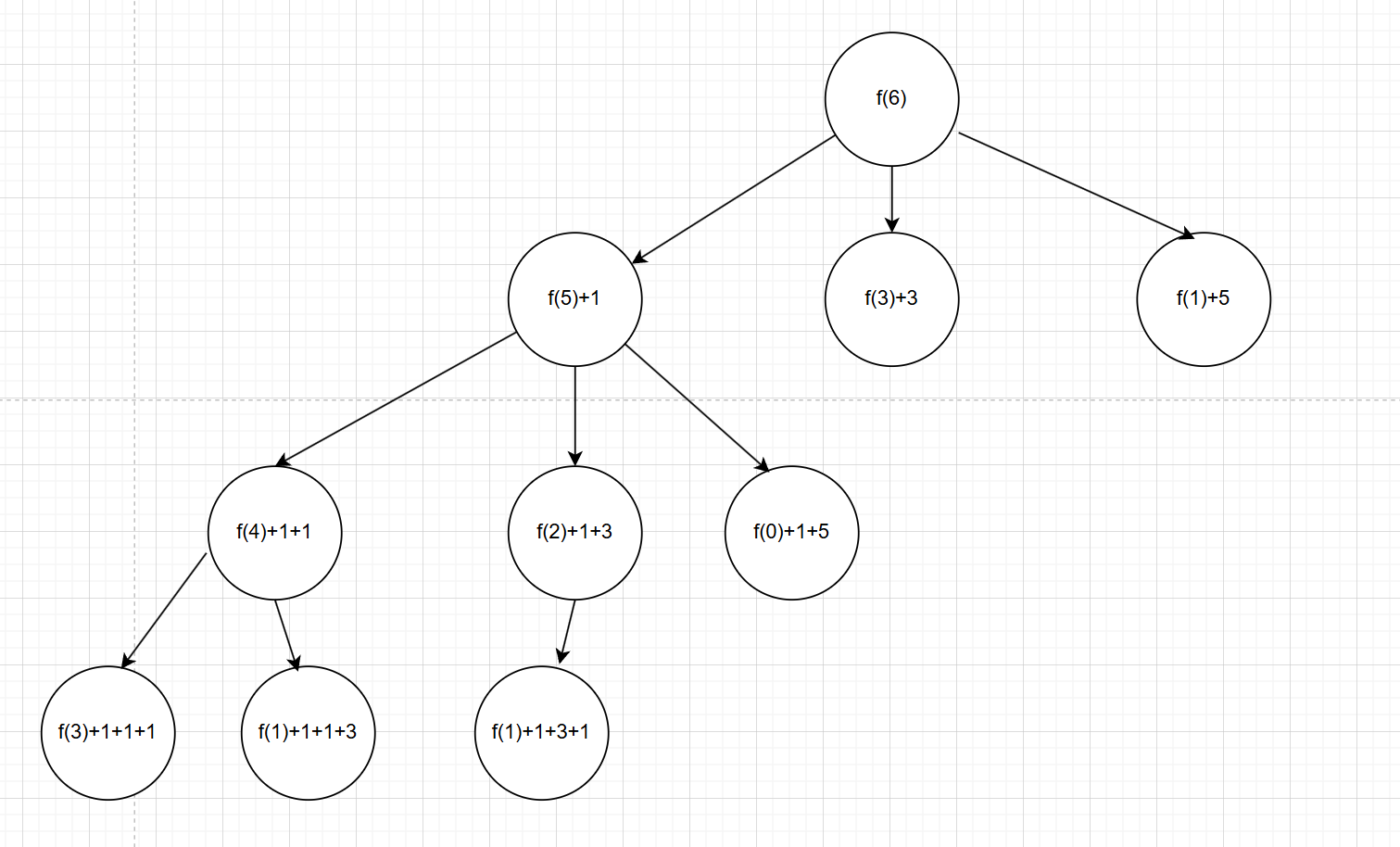
如图，这个题的递归搜索树大致如图，我没有画完全，大致能懂意思就行。

我们可以先写出递归的函数：

int combine01(int n) {if (n < 0) {return 0;}if (n == 1 || n == 0) {return 1;}return combine01(n - 1) + combine01(n - 3) + combine01(n - 5);
}

当n小于0的时候很明显没有组合方式，当n等于1或者n等于0的时候只有一种组合方式。

1. 最后一步采用操作1（步长为1）
   如果最后一步是操作1，那么在此之前需要解决规模为 n-1 的问题

所以有 combine01(n-1) 种方式

2. 最后一步采用操作3（步长为3）
   如果最后一步是操作3，那么在此之前需要解决规模为 n-3 的问题

所以有 combine01(n-3) 种方式

3. 最后一步采用操作5（步长为5）
   如果最后一步是操作5，那么在此之前需要解决规模为 n-5 的问题

所以有 combine01(n-5) 种方式

总和起来就是我们所有的方法数，接下来先采用今天讲的备忘录（记忆化搜索表）实现：

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
static int solve(int n, int *mem) {if (n < 0) {return 0;}if (n == 1 || n == 0) {return 1;}if (mem[n] == -1) {mem[n] = solve(n - 1, mem) + solve(n - 3, mem) + solve(n - 5, mem);}return mem[n];
}int combine02(int n) {int result;int *mem = malloc(sizeof(int) * (n + 1));for (int i = 0; i <= n; ++i) {mem[i] = -1;}result = solve(n, mem);free(mem);return result;
}int main() {printf("%d\n", combine03(6));return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\06_DP\cunNum.exe
8进程已结束，退出代码为 0

再来用DP table的方法：

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
static int solve(int n, int *mem) {if (n < 0) {return 0;}if (n == 1 || n == 0) {return 1;}if (mem[n] == -1) {mem[n] = solve(n - 1, mem) + solve(n - 3, mem) + solve(n - 5, mem);}return mem[n];
}
int combine03(int n) {int *mem = malloc(sizeof(int) * (n + 1));mem[1] = 1;mem[2] = 1;mem[3] = 2;mem[4] = 3;mem[5] = 5;for (int i = 6; i <= n; ++i) {mem[i] = mem[i - 1] + mem[i - 3] + mem[i - 5];}int result = mem[n];free(mem);return result;
}int main() {printf("%d\n", combine03(6));return 0;

结果：

D:\work\DataStruct\cmake-build-debug\06_DP\cunNum.exe
8进程已结束，退出代码为 0

大家可以在LeetCode刷类似的题目，大概先写这些吧，今天的博客就先写到这，谢谢您的观看。