前言
集成学习通过组合多个模型的优势,常能获得比单一模型更优的性能,随机森林便是其中的典型代表。它基于 Bagging 思想,通过对样本和特征的双重随机采样,构建多棵决策树并综合其结果,在降低过拟合风险的同时,显著提升了模型的稳定性与泛化能力。
本文将从随机森林的核心原理出发,结合实战案例对比其与单棵决策树、逻辑回归的性能差异,通过可视化拆解森林内部结构,并总结其优缺点与适用场景,帮助读者快速掌握这一强大算法的核心逻辑与应用方法。
1、随机森林介绍
Bagging 思想 + 决策树就诞生了随机森林(Random Forest)。它通过构建多棵决策树并综合其结果,显著提升了模型的泛化能力和稳定性。
随机森林,都有哪些随机?
- 样本随机:在构建每棵决策树时,采用有放回的随机抽样(bootstrap 抽样)从原始数据集中选取训练样本
- 特征随机:在每个决策树节点分裂时,随机选择部分特征子集,仅从该子集中寻找最优分裂条件
这种双重随机性使得森林中的每棵树都具有一定的差异性,有效降低了单棵决策树容易过拟合的风险,同时通过多棵树的集体决策提高了预测的准确性和稳定性。

随机森林的工作流程可概括为:
-
从原始数据集中通过 bootstrap 抽样生成多个不同的训练子集
-
为每个子集构建一棵决策树,树的每个节点仅使用随机选择的部分特征
-
对于分类问题,通过投票机制综合所有树的预测结果;对于回归问题,则取所有树预测值的平均值
2、随机森林实战
本章将通过具体的代码实现,在经典的鸢尾花数据集上开展实战实验,直观对比随机森林与单棵决策树、逻辑斯蒂回归的性能差异。
2.1、导包加载数据
import numpy as np
from sklearn import tree
from sklearn import datasets
from sklearn.model_selection import train_test_split
import graphviz
# ensemble 集成
# 随机森林
from sklearn.ensemble import RandomForestClassifier
# 作为对照
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
# 加载数据
X,y = datasets.load_iris(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 112)
2.2、普通决策树
score = 0
for i in range(100):X_train,X_test,y_train,y_test = train_test_split(X,y)model = DecisionTreeClassifier()model.fit(X_train,y_train)score += model.score(X_test,y_test)/100
print('随机森林平均准确率是:',score)
单棵决策树的性能受训练数据分割和树结构影响较大,多次运行的结果通常会有较大波动。

2.3、随机森林(运行时间稍长)
score = 0
for i in range(100):X_train,X_test,y_train,y_test = train_test_split(X,y)model = RandomForestClassifier()model.fit(X_train,y_train)score += model.score(X_test,y_test)/100
print('随机森林平均准确率是:',score)
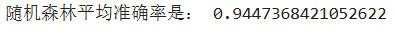
结论:
- 和决策树对比发现,随机森林分数稍高,结果稳定
- 随机森林通过集成多棵树的预测,有效降低了模型的方差,减少了过拟合风险
- 这种稳定性在数据集较小时尤为明显
2.4、逻辑斯蒂回归
import warnings
warnings.filterwarnings('ignore')
score = 0
for i in range(100):X_train,X_test,y_train,y_test = train_test_split(X,y)lr = LogisticRegression()lr.fit(X_train,y_train)score += lr.score(X_test,y_test)/100
print('逻辑斯蒂回归平均准确率是:',score)

结论:
- 不同算法对特定数据集的适应性不同,逻辑斯蒂回归在鸢尾花数据集上表现优秀
- 随机森林作为一种强大的通用算法,在各类数据集上通常都能取得良好表现
- 实际应用中应尝试多种算法并选择最适合当前问题的模型
3、随机森林可视化
3.1、创建随机森林进行预测
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 9)
forest = RandomForestClassifier(n_estimators=100,criterion='gini')
forest.fit(X_train,y_train)
score1 = round(forest.score(X_test,y_test),4)
print('随机森林准确率:',score1)
print(forest.predict_proba(X_test))
随机森林的predict_proba方法返回每个样本属于各个类别的概率,这是通过综合所有决策树的预测结果得到的。
准确率为1.0:

3.2、对比决策树
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 112)
model = DecisionTreeClassifier()
model.fit(X_train,y_train)
print('决策树准确率:',model.score(X_test,y_test))
proba_ = model.predict_proba(X_test)
print(proba_)
准确率为1.0:

总结:
- 一般情况下,随机森林比决策树更加优秀
- 随机森林的predict_proba()返回的是概率分布(如 0.97),反映了模型对预测结果的置信度
- 单棵决策树的predict_proba()返回的是确定值(0 或 1),因为每个样本最终只会落入一个叶节点
3.3、绘制决策树
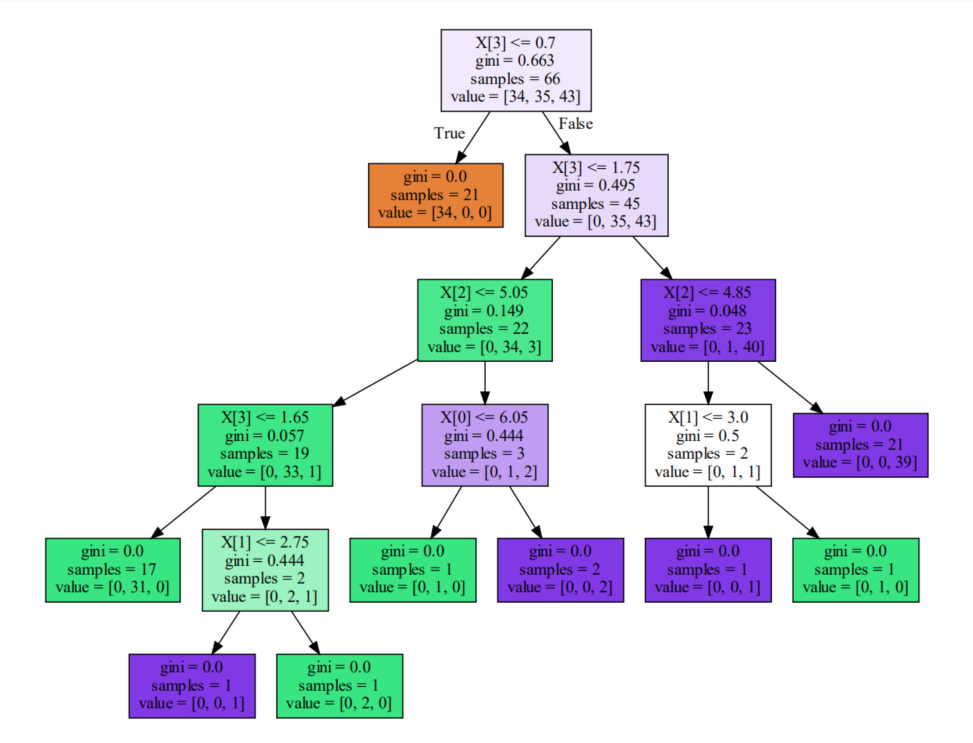
随机森林由多棵决策树组成,我们可以查看其中的部分树来理解森林的多样性:
# 第一颗树类别
dot_data = tree.export_graphviz(forest[0],filled=True)
graph = graphviz.Source(dot_data)
graph
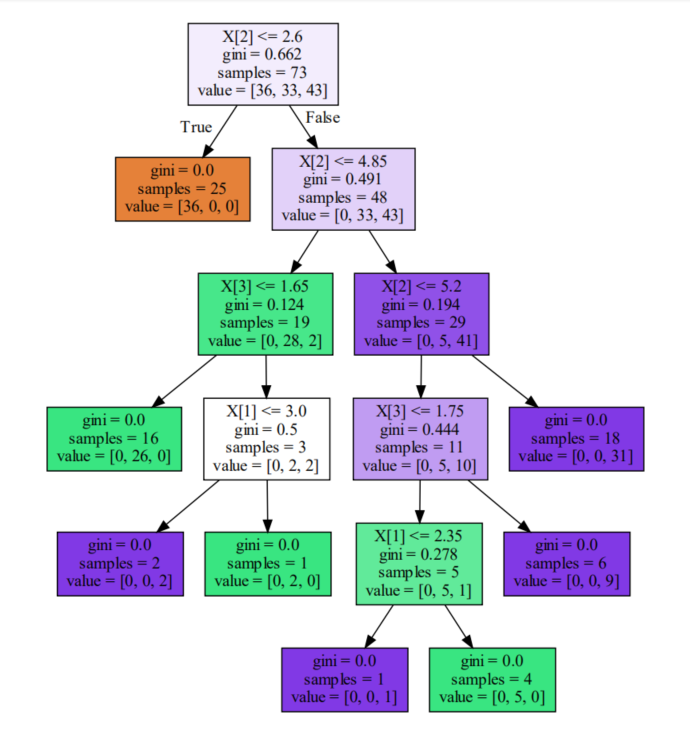
# 第五十颗树类别
dot_data = tree.export_graphviz(forest[49],filled=True)
graph = graphviz.Source(dot_data)
graph
# 第100颗树类别
dot_data = tree.export_graphviz(forest[-1],filled=True)
graph = graphviz.Source(dot_data)
graph
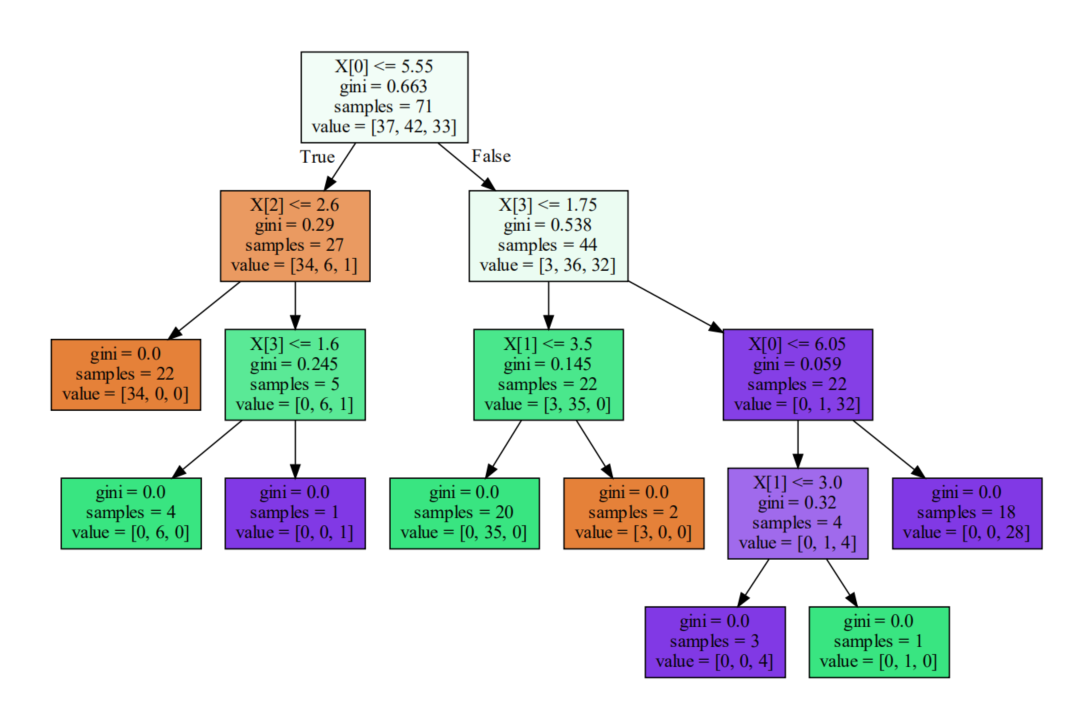
通过对比可以发现,随机森林中的不同决策树在结构和分裂条件上存在差异,这种多样性是随机森林能够提高预测性能的关键。
4、随机森林总结
随机森林主要步骤:
- 随机选择样本:采用有放回抽样(bootstrap)从原始数据集中生成多个训练样本集。
- 随机选择特征:每棵树的每个节点分裂时,仅从随机选择的特征子集中寻找最优分裂条件。
- 构建决策树:为每个样本集构建一棵决策树,不进行剪枝。
- 综合结果:分类问题采用多数投票机制,回归问题采用平均值。
优点:
- 泛化能力强:通过集成多棵树的预测,有效降低了过拟合风险
- 处理高维数据:特征随机选择机制使模型能高效处理高维度数据
- 特征重要性评估:可以输出特征重要性分数,辅助特征选择和数据理解
- 并行计算:树的构建过程相互独立,可并行计算,提高训练效率
- 对缺失值和异常值不敏感:相比其他算法具有更强的鲁棒性
- 适用范围广:既可用于分类问题,也可用于回归问题
缺点:
- 计算成本较高:构建多棵树需要更多计算资源和时间
- 模型解释性差:虽然单棵树易于解释,但多棵树的集成结果难以直观解释
- 对噪声数据敏感:对于噪声过大的数据,仍有可能出现过拟合
- 内存占用较大:存储多棵决策树需要更多内存空间
参数调优关键:
- n_estimators:森林中树的数量,通常越大性能越好,但计算成本也越高。
- max_features:每个节点分裂时考虑的最大特征数,控制特征随机性。
- max_depth:树的最大深度,控制树的复杂度,防止过拟合。
- min_samples_split:分裂内部节点所需的最小样本数。
- min_samples_leaf:叶节点所需的最小样本数。
随机森林作为一种强大而实用的算法,在数据挖掘、机器学习竞赛和工业界都有广泛应用,是解决分类和回归问题的首选算法之一。
经过本章的实战对比,随机森林的优势已然清晰:相比单棵决策树,它用集成的力量提升了稳定性与准确率;面对逻辑斯蒂回归,也展现出强劲的竞争力。
TCP 三握中第三次 ACK 丢失会发生什么?)


)

)
推理部署中的实际显存评估)








全景解析)



