B树与B+树

B树和B+树都是自平衡的多路搜索树，广泛应用于数据库和文件系统中，用于高效管理大量数据。它们的设计目标是在磁盘存储环境下减少I/O操作次数，提高数据访问效率。下面我将逐步解释两者的定义、特性、比较以及应用场景，确保内容清晰易懂。

1. B树简介

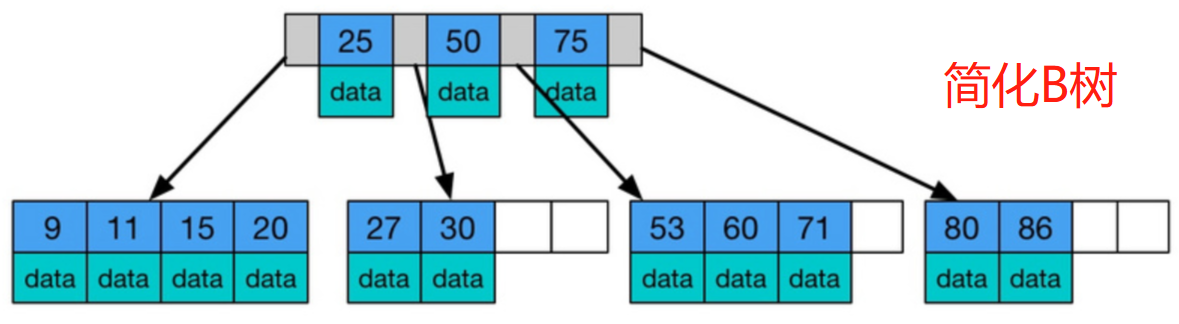
B树（B-tree）是一种平衡树结构，每个节点可以存储多个键值对，并保持有序。它通过分裂和合并节点来维持平衡，确保所有叶子节点处于同一层。B树的关键特性包括：

• 节点结构：每个节点包含多个键值（keys）和指针（pointers）。键值用于搜索，指针指向子节点或数据。
• 度（degree）：B树的最小度t（t \geq 2）定义了节点的键数范围。对于一个节点：
  • 根节点：至少有1个键（除非树为空）。
  • 非根节点：键数在[t-1, 2t-1]之间。
  • 指针数：键数加1。
• 高度平衡：B树的高度h相对较低，通常h = O(log_t n)，其中n是键的总数。这确保了搜索、插入和删除操作的时间复杂度为O(log n)。
• 操作原理：搜索时，从根节点开始，根据键值比较向下遍历；插入时，可能分裂节点；删除时，可能合并节点。

2. B+树简介

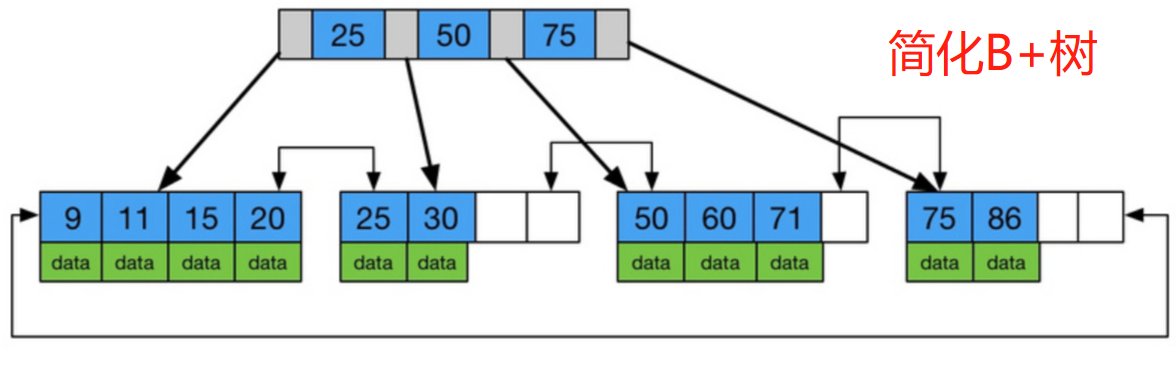
B+树（B-plus tree）是B树的变体，优化了范围查询和顺序访问。它在数据库索引中特别常见，因为所有数据都存储在叶子节点，而内部节点仅作为索引。主要特性包括：

• 节点结构：
  • 内部节点：只存储键值（keys）和指针（pointers），用于路由。
  • 叶子节点：存储键值和实际数据（或数据指针），并通过指针链接成链表，便于顺序扫描。
• 度（degree）：类似于B树，最小度$t$定义了键数范围。叶子节点和非叶子节点的键数都在[t-1, 2t-1]之间（根节点除外）。
• 数据存储：所有数据只在叶子节点中，内部节点不存储数据。这减少了内部节点的空间占用。
• 高度平衡：高度h同样为O(\log_t n)，但范围查询更高效，因为叶子节点是连续的。
• 操作原理：搜索类似B树；插入和删除时，维护叶子节点的链表连接。

1. B树和B+树的定义

B树和B+树都是一种多路搜索树，常用于数据库和文件系统中进行索引操作。在介绍B树和B+树的区别之前，先来了解一下它们的定义。

B树

B树是一种平衡查找树，其每个节点最多包含k个孩子，k称为B树的阶。除根节点和叶子节点外，其它每个节点至少有ceil(k/2)个孩子，即一个节点可以拥有的关键字数在ceil(k/2)和k之间。B树满足以下条件：

• 根节点至少有两个孩子。
• 每个节点最多有k个孩子。
• 除根节点和叶子节点外，其它每个节点至少有ceil(k/2)个孩子。
• 所有叶子节点都在同一层。

B+树

B+树也是一种多路搜索(查找)树，与B树相似，但在B+树中，所有的数据都存储在叶子节点中，而非在非叶子节点中。B+树满足以下条件：

• 所有关键字都出现在叶子节点的链表中，且链表中的关键字恰好是有序的。
• 所有的非叶子节点可以看做是索引部分，节点中仅包含子树中的最大（或最小）关键字。

 

 

 

2. B树与B+树的比较

为了清晰对比，我将两者的主要差异和相似点总结如下表：

特性	B树	B+树
数据存储位置	数据（或数据指针）可存储在所有节点（内部节点和叶子节点）。	数据（或数据指针）仅存储在叶子节点；内部节点只存储键值作为索引。
叶子节点结构	叶子节点独立，无链接。	叶子节点通过指针链接成链表，支持高效顺序访问。
搜索效率	搜索可能在内部节点命中，平均时间复杂度O(logn)。	搜索必须到达叶子节点，但范围查询更优（时间复杂度O(logn + k)，k为结果数）。
空间利用率	内部节点存储数据，可能导致节点更大，I/O次数略高。	内部节点更小（只存键值），能容纳更多键，减少树高度和I/O次数。
插入/删除复杂度	类似，都需要分裂或合并节点，但B树可能更频繁地调整内部数据。	类似，但删除时叶子节点的链表维护更简单。
适用场景	适用于数据量较小或随机查询频繁的系统，如某些文件系统。	更适合数据库索引，尤其范围查询（如SQL的BETWEEN）和全表扫描。

B树和B+树虽然都是多路搜索(查找)树，但它们的区别还是比较明显的。

存储结构

B树的非叶子节点中既包含索引，也包含数据，而B+树的非叶子节点中只包含索引，数据都存储在叶子节点中。这意味着B+树的磁盘I/O操作更少，因为在查询时不需要遍历非叶子节点。

叶子节点

在B树中，每个节点都有指向孩子节点的指针；而在B+树中，只有叶子节点有指针，叶子节点之间通过指针连接起来，形成一个有序链表。

查询性能

B+树的查询性能更优，因为B+树的数据都存储在叶子节点中，而B树的数据既可能存储在非叶子节点中，也可能存储在叶子节点中。B+树在查询时只需要遍历一次叶子节点即可得到查询结果，而B树则需要遍历非叶子节点和叶子节点，效率相对较低。

3. MySQL为什么选择B+树

在MySQL中，索引是用来加速数据查询的，因此索引的设计非常重要。MySQL采用的是B+树作为索引的数据结构，原因如下：

1. B+树的查询性能更好，因为数据都存储在叶子节点中，查询时只需要遍历一次叶子节点即可得到查询结果。
2. B+树的叶子节点之间通过指针连接起来，形成一个有序链表，方便范围查询和排序操作。
3. B+树的非叶子节点中只包含索引，因此占用的空间更小，可以存储更多的索引信息。
4. B+树的阶可以自由调整，可以根据实际情况进行调整，灵活性更高。

4. 总结与应用建议

• B树：在需要快速随机访问的场景中表现良好，例如Ext4文件系统或内存受限环境。但它不擅长范围查询。
• B+树：在数据库管理系统（如MySQL、Oracle）中更常用，因为它优化了顺序访问和范围查询，同时减少了磁盘I/O。

选择建议：

• 如果应用涉及大量范围查询（如数据分析），优先使用B+树。
• 如果数据访问模式以点查询为主，且空间有限，B树可能更合适。