一、题目

介绍：汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
游戏要求：
1、每次只能移动一个圆盘。
2、圆盘只能放置在比它大的圆盘上。
3、圆盘在新的柱子上也是从上到下、从小到大排列。

二、分析

假设n表示个圆盘个数，三根柱子分别用A，B，C进行表示，n个圆盘最初均放在A柱上，我们要将圆盘全部移到C柱上。

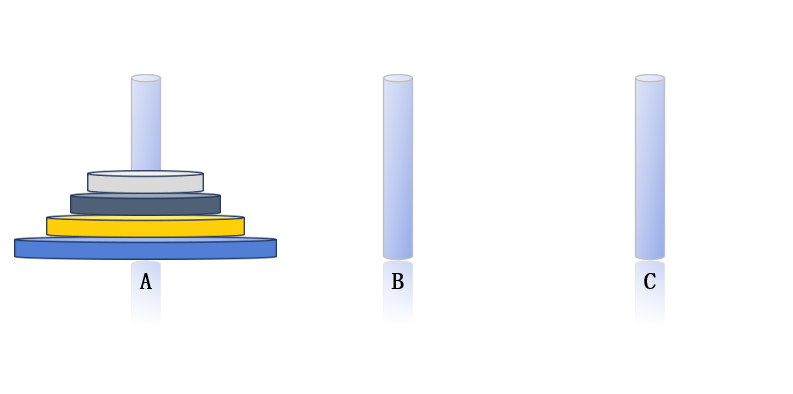
n = 1时，我们只需要1步就能将圆盘移动到C柱：A —> C

n = 2时，需要3步才能将圆盘移动到C柱：A —> B、A —> C、B —> C

n = 3时，需要7步才能将圆盘移动到C柱：A —> C、A —> B、C —> B、A —> C、B —> A、B —> C、A —> C

对于n个圆盘，我们可以参照3个盘子移动的情况，先将A柱上面的n - 1个圆盘通过C柱移动到B柱，剩下最大的那个圆盘直接移动到C柱，B柱上的圆盘通过A柱再移动到C柱上。其需要移动的次数为2^n-1次或者是n - 1个圆盘移动次数乘以2减1。（递归）



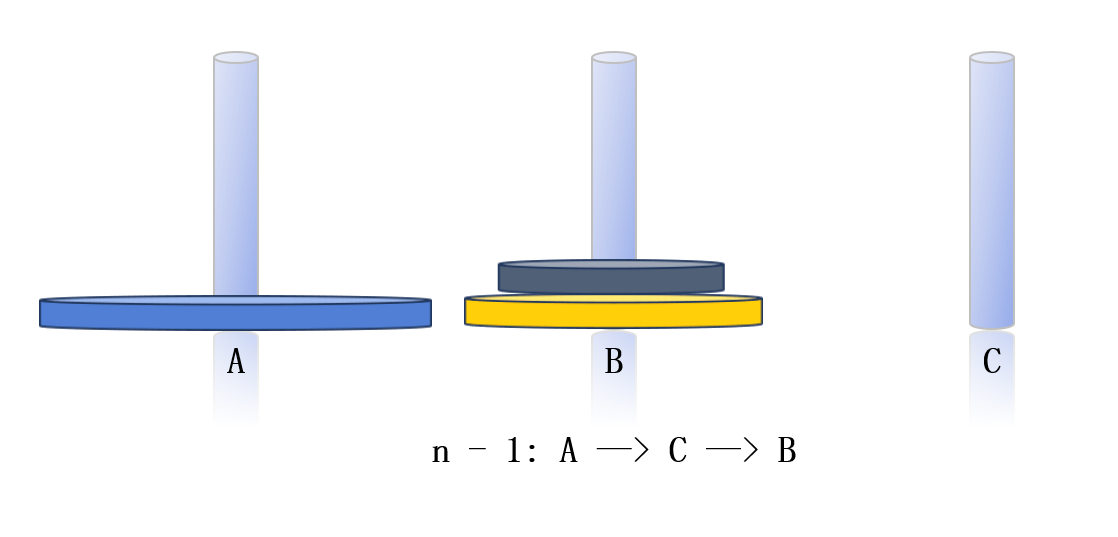
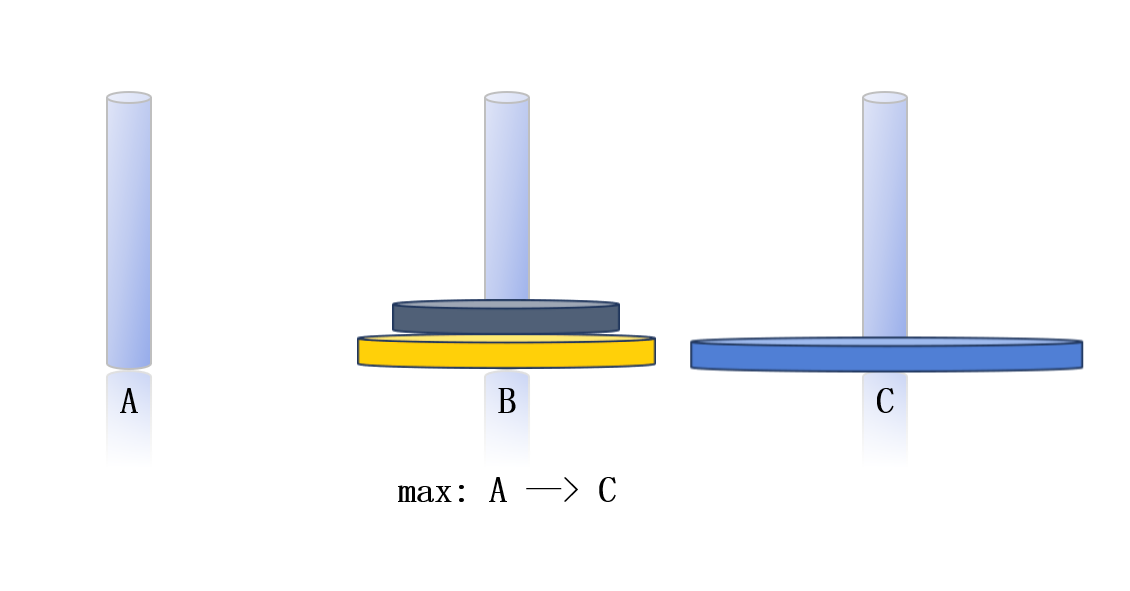
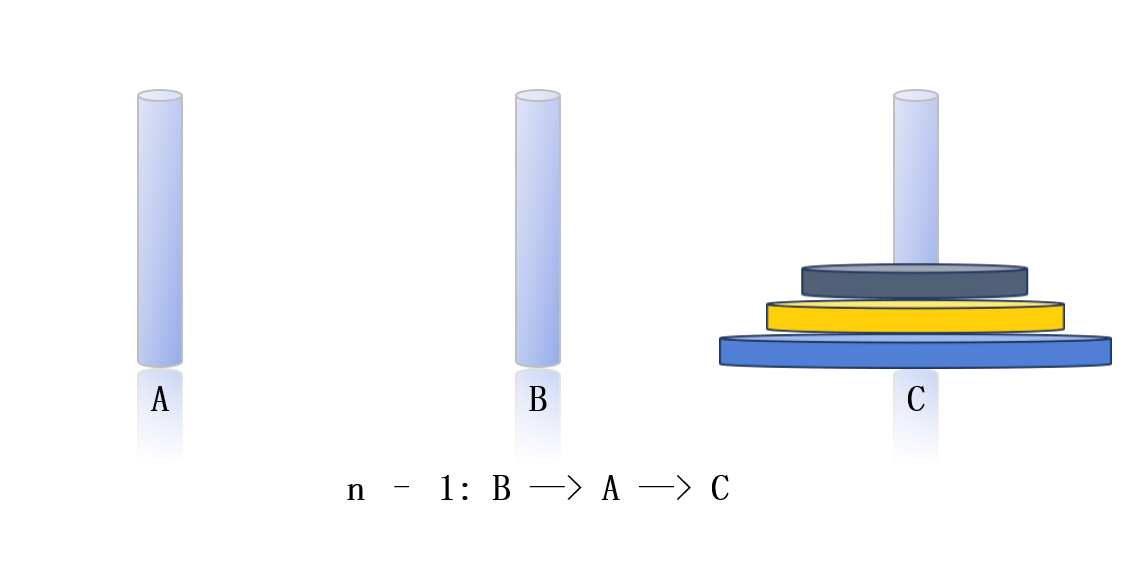
可以把问题看成是把大象塞进冰箱：①打开冰箱门；②把大象关进冰箱；③关上冰箱门

三、代码实现

移动轨迹：

#include <stdio.h>void Move(char x, char y)
{printf("%c ——> %c ", x, y);//移动轨迹
}void Hanoi(int n, char A, char B, char C)
{	if(n ==1)Move(A, C);else{	Hanoi(n - 1, A, C, B);//上面n - 1个通过C柱移动到B柱Move(A, C);//底部最大圆盘直接移动到C柱Hanoi(n - 1, B, A, C);//n - 1个圆盘通过A柱移动到C柱}
}int main()
{int n = 0;scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');//n个圆盘从A柱挪到C柱return 0;
}

运行结果：

移动次数：

#include <stdio.h>int Hanoi(int n)
{if(n == 1)return 1;elsereturn 2 * Hanoi(n - 1) + 1;//移动次数是n - 1个圆盘移动次数乘2减1
}int main()
{int n = 0;scanf("%d", &n);int ret = Hanoi(n);printf("%d", ret);return 0;
}

运行结果：